Sześciokątna rodzina kryształów

Nie mylić z kratą sześciokątną .
Układ kryształów Trójkątny Sześciokątny
System kratowy Rhombohedral.svg
Romboedryczny		 Hexagonal lattice.svg
Sześciokątny
Przykład Dolomite Morocco.jpg
Dolomit 		Kwarc, Madagaskar.jpg
α- kwarc 		Berillo.jpg
Beryl

W krystalografii sześciokątna rodzina kryształów jest jedną z sześciu rodzin kryształów , która obejmuje dwa układy krystaliczne (sześciokątny i trygonalny ) oraz dwa układy sieciowe (sześciokątny i romboedryczny ). Chociaż często mylone, trygonalny system kryształów i romboedryczny system sieci krystalicznej nie są równoważne (patrz sekcja Systemy kryształów poniżej). W szczególności istnieją kryształy, które mają symetrię trygonalną, ale należą do sieci heksagonalnej (takie jak kwarc α ).

Sześciokątna rodzina kryształów składa się z 12 grup punktowych, tak że co najmniej jedna z ich grup przestrzennych ma sześciokątną siatkę jako podstawową sieć i jest połączeniem sześciokątnego układu kryształów i trygonalnego układu kryształów. Jest z nią powiązanych 52 grup przestrzennych, które są dokładnie tymi, których siatka Bravais jest albo sześciokątna, albo romboedryczna.

Systemy kratowe

Sześciokątna rodzina kryształów składa się z dwóch systemów kratowych : heksagonalnego i romboedrycznego. Każdy system sieci składa się z jednej sieci Bravais .

Zależność między dwoma ustawieniami sieci romboedrycznej
Sześciokątna rodzina kryształów
krata Bravais Sześciokątny Romboedryczny
Symbol Pearsona HP godz

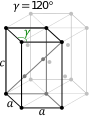
Sześciokątna komórka elementarna 		Hexagonal, primitive Hexagonal, R-centered

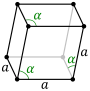
Romboedryczna komórka elementarna 		Rhombohedral, D-centered Rhombohedral, primitive

W rodzinie heksagonalnej kryształ jest konwencjonalnie opisywany przez prostopadłościenną komórkę elementarną graniastosłupa rombowego o dwóch równych osiach ( a na a ) , kącie zawartym 120° ( γ ) i wysokości ( c , która może być różna od a ) prostopadłej do dwóch osi bazowych.

Sześciokątna komórka elementarna dla romboedrycznej sieci Bravais to komórka wyśrodkowana na R, składająca się z dwóch dodatkowych punktów sieci, które zajmują jedną przekątną korpusu komórki elementarnej. Można to zrobić na dwa sposoby, które można traktować jako dwie notacje reprezentujące tę samą strukturę. W zwykłym tak zwanym ustawieniu awersu dodatkowe punkty siatki znajdują się na współrzędnych ( 2 / 3 , 1 / 3 , 1 / 3 ) i ( 1 / 3 , 2 / 3 , 2 / 3 ), podczas gdy w alternatywnym ustawieniu odwrotnym znajdują się one na współrzędnych ( 1 / 3 , 2 / 3 , 1 / 3 ) i ( 2 / 3 , 1 / 3 , 2 / 3 ). W obu przypadkach w sumie na komórkę elementarną przypadają 3 punkty sieci, a sieć nie jest prymitywna.

Sieci Bravais w rodzinie kryształów heksagonalnych można również opisać za pomocą osi romboedrycznych. Komórka elementarna to romboedr (od którego pochodzi nazwa sieci romboedrycznej). To jest komórka elementarna z parametrami a = b = c ; α = β = γ ≠ 90°. W praktyce opis heksagonalny jest częściej używany, ponieważ łatwiej jest poradzić sobie z układem współrzędnych z dwoma kątami 90°. Jednak osie romboedryczne są często pokazywane (dla sieci romboedrycznej) w podręcznikach, ponieważ ta komórka ujawnia 3 m symetria sieci krystalicznej.

Romboedryczna komórka elementarna dla sześciokątnej sieci Bravais to komórka wyśrodkowana na D, składająca się z dwóch dodatkowych punktów sieci, które zajmują jedną przekątną ciała komórki elementarnej o współrzędnych ( 1 / 3 , 1 / 3 , 1 / 3 ) i ( 2 / 3 ) 3 , 2 / 3 , 2 / 3 ). Jednak taki opis jest rzadko używany.

Układy krystaliczne

Układ kryształów Wymagane symetrie grupy punktowej Grupy punktowe Grupy kosmiczne kraty Bravais System kratowy
Trójkątny 1 potrójna oś obrotu 5 7 1 Romboedryczny
18 1 Sześciokątny
Sześciokątny 1 sześciokrotna oś obrotu 7 27

Sześciokątna rodzina kryształów składa się z dwóch układów kryształów : trygonalnego i heksagonalnego. System kryształów to zbiór grup punktów , w których same grupy punktów i odpowiadające im grupy przestrzenne są przypisane do systemu kratowego (patrz tabela w System kryształów #Klasy kryształów ).

Trygonalny system krystaliczny składa się z 5 grup punktowych, które mają pojedynczą potrójną oś obrotu, która obejmuje grupy przestrzenne od 143 do 167. Te 5 grup punktowych ma 7 odpowiednich grup przestrzennych (oznaczonych przez R) przypisanych do układu sieci romboedrycznej i 18 odpowiednie grupy przestrzenne (oznaczone przez P) przypisane do heksagonalnego systemu kratowego. Dlatego trygonalny układ kryształów jest jedynym układem kryształów, którego grupy punktowe mają więcej niż jeden układ sieciowy związany z ich grupami przestrzennymi.

Sześciokątny system kryształów składa się z 7 grup punktowych, które mają pojedynczą sześciokrotną oś obrotu. Te 7 grup punktowych ma 27 grup przestrzennych (168 do 194), z których wszystkie są przypisane do sześciokątnego systemu kratowego.

Trygonalny system kryształów

Poniżej wymieniono 5 grup punktowych w tym systemie kryształów, wraz z ich międzynarodowymi numerami i notacją, ich grupami przestrzennymi w nazwach i przykładowymi kryształami.

Grupa kosmiczna nr. Grupa punktowa Typ Przykłady Grupy kosmiczne
Nazwa Międzynarodowy Schoen. Kula. Sternik. Sześciokątny Romboedryczny
143–146 Piramida trygonalna 3 C 3 33 [3] + polarny enancjomorfik karlinit, jarozyt P3, P3 1 , P3 2 R3
147–148 Romboedryczny 3 do 3i (S 6 ) 3× [2 + ,6 + ] centrosymetryczny dolomit, ilmenit P 3 R 3
149–155 Trapezowy trójkątny 32 D3 _ 223 [2,3] + enancjomorficzny abhuryt , kwarc alfa (152, 154), cynober P312, P321, P3 1 12, P3 1 21, P3 2 12, P3 2 21 R32
156–161 Piramida dwutrygonalna 3m C 3v *33 [3] polarny schorl , ceryt , turmalin , alunit , tantalan litu P3m1, P31m, P3c1, P31c R3m, R3c
162–167 Dwutrygonalny skalenoedryczny 3 m D 3d 2*3 [2 + ,6] centrosymetryczny antymon , hematyt , korund , kalcyt , bizmut 3 1m, 3 1c, 3 1c, 3 m1 , 3 c1 R 3 m, R 3 c

Sześciokątny system kryształów

Poniżej wymieniono 7 grup punktowych ( klas kryształów ) w tym systemie kryształów, a następnie ich reprezentacje w notacji Hermanna-Mauguina lub notacji międzynarodowej i notacji Schoenfliesa oraz przykłady minerałów , jeśli istnieją.

Grupa kosmiczna nr. Grupa punktowa Typ Przykłady Grupy kosmiczne
Nazwa Międzynarodowy Schoen. Kula. Sternik.
168–173 Sześciokątna piramida 6 C 6 66 [6] + polarny enancjomorfik nefelin , kankrynit P6, P6 1 , P6 5 , P6 2 , P6 4 , P6 3
174 Dwupiramid trygonalny 6 C 3 godz 3* [2,3 + ] laurelit i kwas borowy P 6
175–176 Dwupiramid sześciokątny 6/m C 6 godz 6* [2,6 + ] centrosymetryczny apatyt , wanadynit P6/m, P6 3 /m
177–182 Sześciokątny trapez 622 D 6 226 [2,6] + enancjomorficzny kalsilit i wysoki kwarc P622, P6 1 22, P6 5 22, P6 2 22, P6 4 22, P6 3 22
183–186 Dwusześciokątna piramida 6 mm C 6v *66 [6] polarny greenockit , wurcyt P6mm, P6cc, P6 3 cm, P6 3 mc
187–190 Ditrygonalny dwupiramid 6 m2 D 3 godz *223 [2,3] benitoit P 6 m2, P 6 c2, P 6 2m, P 6 2c
191–194 Dwupiramid dwusześciokątny 6/mm D 6 godz *226 [2,6] centrosymetryczny beryl P6/mmm, P6/mcc, P6 3 /mcm, P6 3 /mmc

Sześciokątne ciasno upakowane

Główny artykuł: ścisłe upakowanie równych kulek
Sześciokątna komórka elementarna o ścisłym upakowaniu (hcp).

Sześciokątne upakowanie ścisłe (hcp) jest jednym z dwóch prostych typów upakowania atomów o największej gęstości, drugim jest sześcienny centrowany na twarzy (fcc). Jednak w przeciwieństwie do fcc nie jest to sieć Bravais, ponieważ istnieją dwa nierównoważne zestawy punktów sieci. Zamiast tego można go zbudować z sześciokątnej sieci Bravais przy użyciu motywu dwuatomowego (dodatkowy atom w około ( 2 / 3 , 1 / 3 , 1 / 2 )) związanego z każdym punktem sieci.

Struktury wieloelementowe

Związki, które składają się z więcej niż jednego pierwiastka (np. związki binarne ) często mają struktury krystaliczne oparte na heksagonalnej rodzinie kryształów. Niektóre z bardziej powszechnych są wymienione tutaj. Struktury te można postrzegać jako dwie lub więcej przenikających się podsieci, w których każda podsieć zajmuje miejsca śródmiąższowe pozostałych.

Struktura wurcytu

Zobacz też: Kategoria: Typ struktury wurcytu
Komórka elementarna wurcytu opisana przez operatory symetrii grupy przestrzennej.
Inna reprezentacja komórki elementarnej wurcytu [ potrzebne źródło ]
Inna reprezentacja struktury wurcytu [ potrzebne źródło ]

Struktura krystaliczna wurcytu jest określana przez oznaczenie Strukturbericht B4 i symbol Pearsona hP4. Odpowiednia grupa przestrzenna to nr 186 (w klasyfikacji Międzynarodowej Unii Krystalografii) lub P6 3 mc (w notacji Hermanna – Mauguina ). Symbole Hermanna-Mauguina w P6 3 mc można odczytać następująco:

  • 6 3 .. : sześciokrotny obrót śruby wokół osi c
  • .M. : płaszczyzna lustrzana z normalną {100}
  • ..c : płaszczyzna schodzenia w kierunkach c z normalną {120}.

Wśród związków, które mogą przyjąć strukturę wurcytu, są sam wurcyt ( ZnS zawierający do 8% żelaza zamiast cynku ), jodek srebra (AgI), tlenek cynku (ZnO), siarczek kadmu (CdS), selenek kadmu (CdSe), krzem węglik (α-SiC), azotek galu (GaN), azotek glinu (AlN), azotek boru (w-BN) i inne półprzewodniki . W większości tych związków wurcyt nie jest preferowaną postacią kryształu objętościowego, ale struktura może być preferowana w niektórych nanokrystalicznych postaciach materiału.

W materiałach o więcej niż jednej strukturze krystalicznej przedrostek „w-” jest czasami dodawany do wzoru empirycznego w celu oznaczenia struktury krystalicznej wurcytu, jak w w-BN .

Każdy z dwóch indywidualnych typów atomów tworzy podsieć, która jest heksagonalna zwarta (typ HCP). Patrząc razem, pozycje atomów są takie same jak w lonsdaleicie (sześciokątny diament ). Każdy atom jest tetraedrycznie . Strukturę można również opisać jako sieć HCP cynku z atomami siarki zajmującymi połowę czworościennych pustek lub odwrotnie.

Struktura wurcytu jest niecentrosymetryczna (tzn. nie ma symetrii inwersji ). Z tego powodu kryształy wurcytu mogą (i generalnie mają) mieć właściwości, takie jak piezoelektryczność i piroelektryczność , których brakuje kryształom centrosymetrycznym. [ potrzebne źródło ]

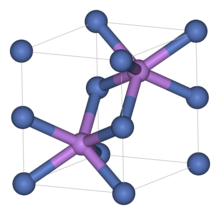
Struktura arsenku niklu

Zobacz też: Kategoria: Typ struktury arsenku niklu

Struktura arsenku niklu składa się z dwóch przenikających się podsieci: prymitywnej heksagonalnej podsieci niklu i heksagonalnej gęsto upakowanej podsieci arsenu. Każdy atom niklu jest oktaedrycznie skoordynowany z sześcioma atomami arsenu, podczas gdy każdy atom arsenu jest trygonalnie skoordynowany pryzmatycznie z sześcioma atomami niklu. Strukturę można również opisać jako sieć HCP z arsenu z niklem zajmującym każdą ośmiościenną pustkę .

Związkami przyjmującymi strukturę NiAs są na ogół chalkogenki , arsenki , antymonki i bizmutydy metali przejściowych . [ potrzebne źródło ]

Komórka elementarna niklu

Oto członkowie grupy Nickeline:

  • Achawalit : FeSe
  • Breithauptyt : NiSb
  • Freboldyt: CoSe
  • Kotulskit: Pd(Te,Bi)
  • Langistyt: (Co,Ni)As
  • Nikiel: NiAs
  • Sobolewskit: Pd(Bi,Te)
  • Sudburyit: (Pd,Ni)Sb

W dwóch wymiarach

Główny artykuł: sześciokątna krata

Jest tylko jedna sześciokątna krata Bravais w dwóch wymiarach: sześciokątna krata.

krata Bravais Sześciokątny
Symbol Pearsona hp
Komórka elementarna 2d hp.svg

Zobacz też

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Hexagonal_crystal_family&oldid=1136712769 ”