Trójkątna ortobicupola
| Trójkątna ortobicupola | |
|---|---|
 | |
| Typ |
Johnson J 26 – J 27 – J 28 |
| Twarze |
2+6 trójkątów 6 kwadratów |
| Krawędzie | 24 |
| Wierzchołki | 12 |
| Konfiguracja wierzchołków | 6(3 2 .4 2 ) 6(3.4.3.4) |
| Grupa symetrii | D 3 godz |
| Podwójny wielościan | Dwunastościan trapezowo-rombowy |
| Nieruchomości | wypukły |
| Internet | |
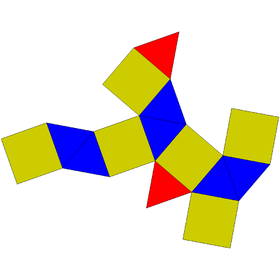 | |
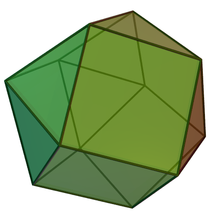
W geometrii trójkątna ortobicupola jest jedną z brył Johnsona ( J 27 ). Jak sama nazwa wskazuje, można ją zbudować, dołączając dwie trójkątne kopuły ( J 3 ) wzdłuż ich podstaw. Ma taką samą liczbę kwadratów i trójkątów w każdym wierzchołku; jednak nie jest przechodnia wierzchołków . Nazywany jest również antykuboośmiościanem , skręconym ośmiościanem sześciennym lub dwuspadowym . Jest to również wielościan kanoniczny .
Bryła Johnsona jest jednym z 92 ściśle wypukłych wielościanów , które składają się z regularnych ścian wielokątów, ale nie są jednolitymi wielościanami (to znaczy nie są bryłami platońskimi , bryłami Archimedesa , graniastosłupami ani antygraniastosłupami ). Zostały one nazwane przez Normana Johnsona , który jako pierwszy wymienił te wielościany w 1966 roku.
Trójkątna ortobicupola jest pierwszą z nieskończonego zestawu ortobicupoli .
Stosunek do kuboktaedry
| Trójkątna ortobicupola | Żyrobiupola trójkątna |
|---|---|

|

|
| Zarówno trójkątna ortobicupola, jak i ośmiościan sześcienny (trójkątna gyrobicupola) zawierają centralny sześciokąt foremny. Można je podzielić na tym sześciokącie na pary trójkątnych kopuł . | |
Trójkątna ortobicupola ma powierzchowne podobieństwo do ośmiościanu sześciennego , który w nomenklaturze brył Johnsona byłby znany jako trójkątna gyrobicupola - różnica polega na tym, że dwie trójkątne kopuły, które tworzą trójkątną ortobicupę, są połączone tak, że pary pasujących boków stykają się ( stąd „orto”); sześcienny ośmiościan jest połączony tak, że trójkąty stykają się z kwadratami i odwrotnie. Biorąc pod uwagę trójkątną ortobikupolę, obrót o 60 stopni jednej kopuły przed połączeniem daje ośmiościan sześcienny. Stąd inna nazwa trójkątnej ortobicupoli to antysześcienny ośmiościan .
Wydłużona trójkątna ortobicupola ( J 35 ), która jest zbudowana przez wydłużenie tej bryły, ma (inny) szczególny związek z ośmiościanem rombowym .
Podwójna trójkątna ortobicupola to dwunastościan trapezowo-rombowy . Ma 6 rombowych i 6 trapezowych ścian i jest podobny do dwunastościanu rombowego .
Formuły
Poniższe wzory na objętość , pole powierzchni i promień obwodu można zastosować, jeśli wszystkie ściany są regularne i mają długość krawędzi a :
Promień okręgu trójkątnej ortobicupoli jest taki sam jak długość krawędzi ( C = a ).
Powiązane wielościany i plastry miodu
sześcienny plaster miodu można rozciąć i odbudować jako wypełniającą przestrzeń kratę trójkątnych ortobikupoli i kwadratowych piramid .

