Wydłużona kwadratowa gyrobicupola
| Wydłużona kwadratowa gyrobicupola | |
|---|---|
 | |
| Typ |
Johnson J 36 – J 37 – J 38 |
| Twarze |
8 trójkątów 18 kwadratów |
| Krawędzie | 48 |
| Wierzchołki | 24 |
| Konfiguracja wierzchołków | 8+16(3,4 3 ) |
| Grupa symetrii | D 4d |
| Podwójny wielościan | Icositetrahedron pseudo-naramienny |
| Nieruchomości | wypukła , pojedyncza figura wierzchołka , kanoniczna |
| Internet | |
 | |
W geometrii wydłużona kwadratowa gyrobicupola lub pseudo-rombicuboctahedr jest jedną z brył Johnsona ( J 37 ). Zwykle nie jest uważana za bryłę Archimedesa , mimo że jej ściany składają się z regularnych wielokątów , które spotykają się w tym samym wzorze w każdym z jej wierzchołków , ponieważ w przeciwieństwie do 13 brył Archimedesa brakuje jej zestawu globalnych symetrii , które odwzorowują każdy wierzchołek na co drugi wierzchołek (chociaż Grünbaum zasugerował, że powinien zostać dodany do tradycyjnej listy brył Archimedesa jako 14. przykład). Bardzo przypomina, ale nie należy go mylić z ośmiościanem rombowym , który jest bryłą Archimedesa. Jest to również wielościan kanoniczny .
Kształt ten mógł zostać odkryty przez Johannesa Keplera podczas wyliczania brył Archimedesa, ale jego pierwsze wyraźne pojawienie się w druku wydaje się być dziełem Duncana Sommerville'a w 1905 r. Został on niezależnie ponownie odkryty przez JCP Millera do 1930 r. (przez pomyłkę podczas próby zbudować model ośmiościanu rombu ) i ponownie przez VG Ashkinuse w 1957 roku.
Bryła Johnsona jest jednym z 92 ściśle wypukłych wielościanów , które składają się z regularnych ścian wielokątów, ale nie są jednolitymi wielościanami (to znaczy nie są bryłami platońskimi , bryłami Archimedesa , graniastosłupami ani antygraniastosłupami ). Zostały one nazwane przez Normana Johnsona , który jako pierwszy wymienił te wielościany w 1966 roku.
Budowa i związek z ośmiościanem rombowym
Jak sama nazwa wskazuje, można go zbudować, wydłużając kwadratową gyrobicupolę ( J 29 ) i wstawiając między jej dwie połówki ośmiokątny pryzmat .
 Ośmiościan rombowy: trójkąty (na niebiesko) są ustawione pionowo |
 Eksplodowane sekcje ośmiościanu rombu |
 pseudorombowy : trójkąty są ułożone naprzemiennie w pionie |
Bryłę można również postrzegać jako wynik skręcenia jednej z kwadratowych kopuł ( J 4 ) na ośmiościanie rombu (jednej z brył Archimedesa , czyli wydłużonej kwadratowej ortokopuły) o 45 stopni. Jest to zatem wirowaty ośmiościan rombowy . Jego podobieństwo do ośmiościanu rombu daje mu alternatywną nazwę pseudo-ośmiościan rombu . Czasami nazywano ją „czternastą bryłą Archimedesa”.
Ta właściwość nie przenosi się na jego odpowiednik o pięciokątnej twarzy, wirowaty rombicozydodekahedron .
Symetria i klasyfikacja
Pseudo-rombowy ośmiościan ma symetrię D 4d . Jest lokalnie regularny wierzchołkowo - układ czterech ścian incydentnych na dowolnym wierzchołku jest taki sam dla wszystkich wierzchołków; jest to wyjątkowe wśród ciał stałych Johnsona. Jednak sposób, w jaki jest „skręcony”, nadaje mu odrębny „równik” i dwa odrębne „bieguny”, które z kolei dzielą jego wierzchołki na 8 wierzchołków „biegunowych” (4 na biegun) i 16 wierzchołków „równikowych”. Dlatego nie jest przechodnia przez wierzchołki , a co za tym idzie, zwykle nie jest uważana za jedną z brył Archimedesa .
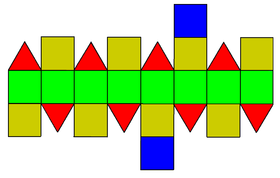
Z twarzami pokolorowanymi według symetrii D 4d może wyglądać tak:
| Pseudo -naramienny icositetrahedron (po prawej) to podwójny wielościan . | |
 
|
 
|
równika znajduje się 8 (zielonych) kwadratów , 4 (czerwone) trójkąty i 4 (żółte) kwadraty powyżej i poniżej oraz jeden (niebieski) kwadrat na każdym biegunie.
Powiązane wielościany i plastry miodu
Wydłużona kwadratowa gyrobicupola może tworzyć wypełniający przestrzeń plaster miodu z regularnym czworościanem , sześcianem i ośmiościanem sześciennym . Może również tworzyć kolejny plaster miodu z czworościanem, kwadratową piramidą i różnymi kombinacjami sześcianów, wydłużonymi kwadratowymi piramidami i wydłużonymi kwadratowymi dwupiramidami .

Pseudo -wielki rombowy-ośmiościan jest niewypukłym analogiem pseudo-rombikubo-ośmiościanu, zbudowanym w podobny sposób z niewypukłego wielkiego rombu-ośmiościanu .
w chemii
Jon poliwanadanowy [ V 18 O 42 ] 12− ma strukturę pseudo-rombikubo-oktaedryczną, w której każda kwadratowa ściana działa jak podstawa piramidy VO 5 .
Dalsza lektura
- Anthony Pugh (1976), Wielościany: podejście wizualne , Kalifornia: University of California Press Berkeley, ISBN 0-520-03056-7 Rozdział 2: Wielościany Archimedesa, pryzmaty i antygraniastosłupy, s. 25 Ośmiościan pseudorombowy

