Snub kwadratowy antypryzmat

Snub kwadratowy antypryzmat
Typ	Johnson J 84 – J 85 – J 86
Twarze	8+16 trójkątów 2 kwadraty
Krawędzie	40
Wierzchołki	16
Konfiguracja wierzchołków	8(3 5 ) 8(3 4 , 4)
Grupa symetrii	D 4d
Podwójny wielościan	-
Nieruchomości	wypukły
Internet

Model 3D kwadratowego antygraniastosłupa

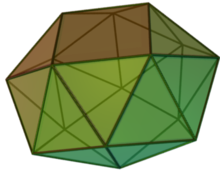
W geometrii zadarty kwadratowy antygraniastosłup jest jedną z brył Johnsona ( J ₈₅ ). Bryła Johnsona jest jednym z 92 ściśle wypukłych wielościanów , które składają się z regularnych ścian wielokątów, ale nie są jednolitymi wielościanami (to znaczy nie są bryłami platońskimi , bryłami Archimedesa , graniastosłupami ani antygraniastosłupami ). Zostały nazwane przez Normana Johnsona , który jako pierwszy wymienił te wielościany w 1966 roku.

Jest to jedna z elementarnych brył Johnsona, które nie powstają w wyniku manipulacji „wytnij i wklej” brył platońskich i archimedesowych , chociaż jest krewnym dwudziestościanu , który ma czterokrotną symetrię zamiast trzykrotnej.

Budowa

Kwadratowy antygraniastosłup prosty jest skonstruowany tak, jak sugeruje jego nazwa, kwadratowy antygraniastosłup , który jest odcięty i przedstawiony jako ss{2,8}, z s{2,8} jako kwadratowy antygraniastosłup . Można go skonstruować w notacji wielościanów Conwaya jako sY4 ( zadarta piramida kwadratowa ).

Można go również skonstruować jako kwadratową kopułę gyrobianticupolae , łączącą dwie antykopuły z wirującymi orientacjami.

współrzędne kartezjańskie

Niech k ≈ 0,82354 będzie dodatnim pierwiastkiem wielomianu sześciennego

${\ Displaystyle 9x ^ {3} + 3 {\ sqrt {3}} \ lewo (5- {\ sqrt {2}} \ prawo) x ^ {2} -3 \ lewo (5-2 {\ sqrt {2} }}\right)x-17{\sqrt {3}}+7{\sqrt {6}}.}$

Ponadto niech h ≈ 1,35374 będzie określone przez

${\ Displaystyle h = {\ Frac {{\ sqrt {2}} + 8 + 2 {\ sqrt {3}} k-3 \ lewo (2 + {\ sqrt {2}} \ prawej) k ^ {2} }{4{\sqrt {3-3k^{2}}}}}.}$

Następnie współrzędne kartezjańskie antygraniastosłupa prostego kwadratowego o długości krawędzi 2 są dane przez sumę orbit punktów

${\ Displaystyle (1,1, h), \, \ lewo (1 + {\ sqrt {3}} k, 0,h-{\sqrt {3-3k^{2}}}\right)}$

pod działaniem grupy wywołanym przez obrót wokół osi z o 90° i obrót o 180° wokół prostej prostopadłej do osi z i tworzącej z osią x kąt 22,5° .

Możemy wtedy obliczyć pole powierzchni antygraniastosłupa prostego kwadratowego o długości krawędzi a as

${\ Displaystyle A = \ lewo (2 + 6 {\ sqrt {3}} \ prawej) a ^ {2} \ około 12,39230a ^ {2}, }$

a jego objętość jako

${\ Displaystyle V = \ xi a ^ {3},}$

gdzie ξ ≈ 3,60122 jest największym rzeczywistym pierwiastkiem wielomianu

$^ {6} + 1158 8832x^{4}+4759488x ^{2}-892448.}$

Snub antypryzmaty

Podobnie skonstruowany, ss{2,6} jest trójkątnym antygraniastosłem prostym ( ośmiościan o niższej symetrii ) i daje w rezultacie dwudziestościan foremny . Zadarty pięciokątny antygraniastosłup , ss{2,10} lub wyższy n -antygraniastosłup może mieć podobną konstrukcję, ale nie jako wypukły wielościan z trójkątami równobocznymi. Poprzednia bryła Johnsona, zadarty disfenoid również pasuje konstrukcyjnie jako ss{2,4}, ale należy zachować dwie zdegenerowane ściany dwukątne (zaznaczone na czerwono) w antygraniastosłupie dwukątnym .

Snub antypryzmaty

Symetria	re 2d , [2 + ,4], (2*2)	re 3d , [2 + ,6], (2*3)	re 4d , [2 + ,8], (2*4)	re 5d , [2 + ,10], (2*5)
Antypryzmaty	s{2,4} A2 (w:4; e:8; f:6)	s{2,6} A3 (w:6; e:12; f:8)	s{2,8} A4 (w:8; e:16; f:10)	s{2,10} A5 (w:10; e:20; f:12)
Ścięte antypryzmaty	ts{2,4} tA2 (v:16;e:24;f:10)	ts{2,6} tA3 (w:24; t:36; f:14)	ts{2,8} tA4 (w:32; t:48; f:18)	ts{2,10} tA5 (v:40; t:60; f:22)
Symetria	re 2 , [2,2] + , (222)	re 3 , [3,2] + , (322)	re 4 , [4,2] + , (422)	re5 , [5,2] + , (522)
Snub antypryzmaty	J84	dwudziestościan	J85	Wklęsły
		sY3 = HtA3	sY4 = HtA4	sY5 = HtA5
	ss{2,4} (w:8; e:20; f:14)	ss{2,6} (w:12; w:30; w:20)	ss{2,8} (w:16; t:40; f:26)	ss{2,10} (w:20; t:50; f:32)

Linki zewnętrzne

• Eric W. Weisstein , antypryzmat kwadratowy Snub ( bryła Johnsona ) w MathWorld .