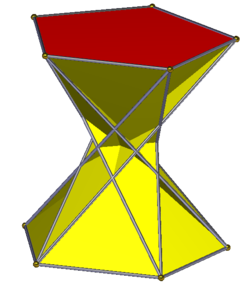
Pięciokątny antypryzmat
| Jednolity pięciokątny antygraniastosłup | |
|---|---|

|
|
| Typ | Pryzmatyczny jednolity wielościan |
| Elementy |
F = 12, E = 20 V = 10 (χ = 2) |
| Twarze po bokach | 10{3}+2{5} |
| Symbol Schläfliego |
s{2,10} sr{2,5} |
| Symbol Wythoffa | | 2 2 5 |
| Diagram Coxetera |
|
| Grupa symetrii | D 5d , [2 + ,10], (2*5), rząd 20 |
| Grupa rotacyjna | D 5 , [5,2] + , (522), rząd 10 |
| Bibliografia | U 77(c) |
| Podwójny | Trapez pięciokątny |
| Nieruchomości | wypukły |
 Rysunek wierzchołka 3.3.3.5 |
|
W geometrii pięciokątny antygraniastosłup jest trzecim z nieskończonego zestawu antygraniastosłupów utworzonych przez parzystą sekwencję boków trójkąta zamkniętych dwoma wielokątami. Składa się z dwóch pięciokątów połączonych ze sobą pierścieniem dziesięciu trójkątów , co daje w sumie dwanaście ścian. Jest to więc dwunastościan nieregularny .
Geometria
Jeśli ściany pięciokątnego antygraniastosłupa są regularne, jest to wielościan półregularny . Można go również uznać za parabidyminowany dwudziestościan , kształt utworzony przez usunięcie dwóch pięciokątnych piramid z regularnego dwudziestościanu, pozostawiając dwie niesąsiadujące pięciokątne ściany; pokrewny kształt, metabidyminowany dwudziestościan (jedna z brył Johnsona ), podobnie powstaje z dwudziestościanu przez usunięcie dwóch ostrosłupów, ale jego pięciokątne ściany przylegają do siebie. Dwie pięciokątne ściany o dowolnym kształcie można powiększyć piramidami, tworząc dwudziestościan.
Stosunek do polytopów
Pięciokątny antygraniastosłup występuje jako element składowy niektórych politopów o wyższych wymiarach . Dwa pierścienie po dziesięć pięciokątnych antygraniastosłupów ograniczały hiperpowierzchnię czterowymiarowego wielkiego antygraniastosłupa . Jeśli te antygraniastosłupy zostaną powiększone pięciokątnymi piramidami graniastosłupowymi i połączone pierścieniami po pięć czworościanów każdy, otrzymamy 600 komórek .
Zobacz też
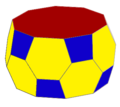
Pięciokątny antygraniastosłup można obcinać i układać naprzemiennie, tworząc zadarty antygraniastosłup :
|
Antypryzmat A5 |
Obcięty tA5 |
Naprzemienne htA5 |
|---|---|---|

|
|

|
| s{2,10} | ts{2,10} | ss{2,10} |
| werset 10; e:20; f:12 | werset:40; e:60; f:22 | werset 20; e:50; f:32 |
| Nazwa antypryzmatu | Digonalny antypryzmat |
(Trójkątny) Trójkątny antygraniastosłup |
(Czworokąt) Kwadratowy antygraniastosłup |
Pięciokątny antypryzmat | Sześciokątny antypryzmat | Siedmiokątny antypryzmat | Ośmiokątny antypryzmat | Enneagonalny antypryzmat | Dekagonalny antypryzmat | Sześciokątny antygraniastosłup | Dwunastokątny antypryzmat | ... | Antygraniastosłup apeirogonalny |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Obraz wielościanu |
|
|
|
|
|
|
|
|
|
|
|
... | |
| Sferyczny obraz kafelkowy |
|
|
|
|
|
|
|
Obraz kafelkowy samolotu |
|
||||
| Konfiguracja wierzchołków. | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3.3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | ... | ∞.3.3.3 |
Przekreślony antypryzmat
Skrzyżowany pięciokątny antygraniastosłup jest topologicznie identyczny z pięciokątnym antygraniastosłupem , chociaż nie można go ujednolicić. Boki to trójkąty równoramienne . Ma symetrię d 5d , rząd 10. Jego konfiguracja wierzchołków to 3,3/2,3,5, z jednym trójkątem wstecznym, a układ wierzchołków jest taki sam jak graniastosłup pięciokątny .
Linki zewnętrzne
- Weisstein, Eric W. „Antypryzmat” . MathWorld .
- [1]
- Antygraniastosłup pięciokątny: interaktywny model wielościanu
- Wirtualna rzeczywistość Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
- wielościan A5