Siedmiokątny antypryzmat

Jednolity siedmiokątny antygraniastosłup

Typ	Pryzmatyczny jednolity wielościan
Elementy	F = 16, E = 28 V = 14 (χ = 2)
Twarze po bokach	14{3}+2{7}
Symbol Schläfliego	s{2,14} sr{2,7}
Symbol Wythoffa	\| 2 2 7
Diagram Coxetera
Grupa symetrii	D _7d , [2 ⁺ ,14], (2*7), rząd 28
Grupa rotacyjna	D ₇ , [7,2] ⁺ , (722), rząd 14
Bibliografia	U _77(e)
Podwójny	Siedmiokątny trapez
Nieruchomości	wypukły
Rysunek wierzchołka 3.3.3.7

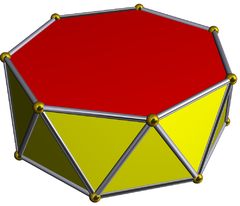
W geometrii siedmiokątny antygraniastosłup jest piątym z nieskończonego zestawu antygraniastosłupów utworzonych przez parzystą sekwencję boków trójkąta zamkniętych dwoma wielokątami.

Antypryzmaty są podobne do pryzmatów , z wyjątkiem tego, że podstawy są skręcone względem siebie, a ściany boczne są trójkątami, a nie czworobokami.

W przypadku zwykłej 7-bocznej podstawy zwykle rozważa się przypadek, gdy jej kopia jest skręcona o kąt 180°/ n . Dodatkową regularność uzyskuje się dzięki temu, że linia łącząca środki podstaw jest prostopadła do płaszczyzn podstawowych, co czyni ją prawym antygraniastosłupem . Jako ściany ma dwie n -kątne podstawy i, łącząc te podstawy, 2 n trójkątów równoramiennych.

Jeśli wszystkie ściany są regularne, jest to wielościan półregularny .

Zobacz też

Rodzina jednorodnych antypryzmatów n -gonalnych
Nazwa antypryzmatu	Digonalny antypryzmat	(Trójkątny) Trójkątny antygraniastosłup	(Czworokąt) Kwadratowy antygraniastosłup	Pięciokątny antypryzmat	Sześciokątny antypryzmat	Siedmiokątny antypryzmat	Ośmiokątny antypryzmat	Enneagonalny antypryzmat	Dekagonalny antypryzmat	Sześciokątny antygraniastosłup	Dwunastokątny antypryzmat	...	Antygraniastosłup apeirogonalny
Obraz wielościanu												...
Sferyczny obraz kafelkowy												Obraz kafelkowy samolotu
Konfiguracja wierzchołków.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3

Linki zewnętrzne

Wirtualna rzeczywistość Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
- Model VRML
wielościan A7