Dwunastościan ścięty

Dwunastościan ścięty
(kliknij tutaj, aby zobaczyć obracający się model)
Typ	Bryła Archimedesa Jednolity wielościan
Elementy	F = 32, E = 90, V = 60 (χ = 2)
Twarze po bokach	20{3}+12{10}
Notacja Conwaya	tD
symbole Schläfliego	t{5,3}
	t 0,1 {5,3}
Symbol Wythoffa	2 3 | 5
Diagram Coxetera
Grupa symetrii	I h , H 3 , [5,3], (*532), rząd 120
Grupa rotacyjna	I , [5,3] + , (532), rząd 60
Kąt dwuścienny	10-10: 116,57° 3-10: 142,62°
Bibliografia	U 26 , C 29 , W 10
Nieruchomości	Półregularny wypukły
Kolorowe twarze	3.10.10 ( rysunek wierzchołka )
Triakis dwudziestościan ( podwójny wielościan )	Internet

Model 3D ściętego dwunastościanu

W geometrii dwunastościan ścięty jest bryłą Archimedesa . Ma 12 regularnych dziesięciokątnych ścian, 20 regularnych trójkątnych ścian, 60 wierzchołków i 90 krawędzi.

Relacje geometryczne

Ten wielościan można utworzyć z dwunastościanu foremnego przez obcięcie (odcięcie) rogów, tak aby ściany pięciokąta stały się dziesięciokątami , a rogi trójkątami .

Jest używany w hiperbolicznej teselacji wypełniającej przestrzeń przechodniów komórkowych , dwudziestościennym plastrze miodu z bitruncated .

Powierzchnia i objętość

Pole powierzchni A i objętość V dwunastościanu ściętego o długości krawędzi a wynoszą:

${\ Displaystyle {\ rozpocząć {wyrównane} A & = 5 \ lewo ({\ sqrt {3}} + 6 {\ sqrt {5 + 2 {\ sqrt {5}}}} \ prawej) a ^ {2} & & \ około 100,990\,76a^{2}\\V&={\tfrac {5}{12}}\left(99+47{\sqrt {5}}\right)a^{3}&&\około 85,039\, 6646a^{3}\end{wyrównane}}}$

współrzędne kartezjańskie

Współrzędne kartezjańskie wierzchołków dwunastościanu ściętego o długości krawędzi 2 φ - 2, wyśrodkowane w początku, są parzystymi permutacjami:

(0, ± 1 / φ , ±(2 + φ ))

(± 1 / φ , ± φ , ±2 φ )

(± φ , ±2, ±( φ + 1))

gdzie φ = 1 √ 5/2 to . + złoty podział

Projekcje ortogonalne

Dwunastościan ścięty ma pięć specjalnych rzutów prostopadłych , wyśrodkowanych: na wierzchołku, na dwóch rodzajach krawędzi i dwóch rodzajach ścian. Dwa ostatnie odpowiadają płaszczyznom _A2 i _H2 Coxetera .

Projekcje ortogonalne

Wyśrodkowany przez	Wierzchołek	Krawędź 3-10	Krawędź 10-10	Trójkąt twarzy	Dekagon twarzy
Solidny
szkielet
Symetria projekcyjna	[2]	[2]	[2]	[6]	[10]
Podwójny

Nachylenia sferyczne i diagramy Schlegla

Dwunastościan ścięty może być również przedstawiony jako sferyczna płytka i rzutowany na płaszczyznę za pomocą projekcji stereograficznej . Ta projekcja jest konforemna , zachowując kąty, ale nie obszary lub długości. Linie proste na kuli są rzutowane na płaszczyznę jako okrągłe łuki.

Diagramy Schlegla są podobne, z rzutem perspektywicznym i prostymi krawędziami.

Projekcja ortograficzna	Projekcje stereograficzne
	Wyśrodkowany w dziesięcioboku	Wyśrodkowany trójkąt

Układ wierzchołków

Dzieli swój układ wierzchołków z trzema niewypukłymi jednolitymi wielościanami :

Dwunastościan ścięty

Wielki icosicosidodecahedron

Wielki dwunastościan dwutrygonalny dwunastościan

Wielki dwunastościan

Powiązane wielościany i tilings

Jest to część procesu obcinania między dwunastościanem a dwudziestościanem:

Rodzina jednolitych dwudziestościanów wielościanów
Symetria : [5,3] , (*532)							[5,3] + , (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rrr{5,3}	tr{5,3}	sr{5,3}
Podwójne do jednolitych wielościanów
V5.5.5	Wersja 3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Wielościan ten jest spokrewniony topologicznie jako część ciągu jednorodnych wielościanów ściętych o konfiguracjach wierzchołków (3.2 n .2 n ) i [ n ,3] symetrii grupy Coxetera .

* n 32 mutacja symetrii ściętych nachyleń kulistych: t{ n ,3}
Symetria * n 32 [n,3]	Kulisty				Euklides.	Kompaktowy hiperb.		Parako.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Postacie obcięte
Symbol	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	t{∞,3}
Figurki Triakisa
Konfig.	Wersja 3.4.4	V3.6.6	V3.8.8	Wersja 3.10.10	Wersja 3.12.12	Wersja 3.14.14	Wersja 3.16.16	V3.∞.∞

Obcięty wykres dwunastościenny

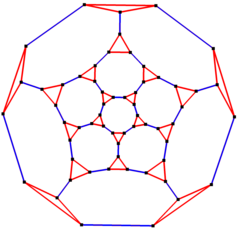
Diagram Schlegla o 5-krotnej symetrii
obcięty dwunastościenny
Wierzchołki	60
Krawędzie	90
Automorfizmy	120
Liczba chromatyczna	2
Nieruchomości	Sześcienny , hamiltonowski , regularny , zero-symetryczny
Tabela wykresów i parametrów

W matematycznej dziedzinie teorii grafów , graf dwunastościanu ściętego to wykres wierzchołków i krawędzi dwunastościanu ściętego , jednej z brył Archimedesa . Ma 60 wierzchołków i 90 krawędzi i jest sześciennym grafem Archimedesa .

Okólnik

Notatki

•   Williams, Robert (1979). Geometryczne podstawy naturalnej struktury: źródłowa księga projektowania . Dover Publications, Inc. ISBN 0-486-23729-X . (Sekcja 3-9)
•   Cromwell, P. (1997). Wielościany . Wielka Brytania: Cambridge. s. 79–86 Bryły Archimedesa . ISBN 0-521-55432-2 .

Linki zewnętrzne

• Eric W. Weisstein , Dwunastościan ścięty ( bryła Archimedesa ) w MathWorld .
  • Weisstein, Eric W. „Obcięty wykres dwunastościenny” . MathWorld .
• Klitzing, Richard. „3D wypukłe jednolite wielościany o3x5x - tid” .
• Edytowalna siatka dwunastościanu ściętego do druku z interaktywnym widokiem 3D
• Jednolite wielościany
• Wielościany wirtualnej rzeczywistości Encyklopedia wielościanów