Jednolity wielościan gwiazdy


W geometrii jednolity wielościan gwiazdy jest samoprzecinającym się jednolitym wielościanem . Czasami nazywane są również wielościanami niewypukłymi , aby sugerować samoprzecinające się. Każdy wielościan może zawierać wielokąta gwiazdy , figury wierzchołków wielokąta gwiazdy lub oba te elementy.
Kompletny zestaw 57 niepryzmatycznych jednorodnych wielościanów gwiazd obejmuje 4 regularne, zwane wielościanami Keplera-Poinsota , 5 quasiregularnych i 48 półregularnych.
Istnieją również dwa nieskończone zestawy jednorodnych pryzmatów gwiazdowych i jednorodnych antygraniastosłupów gwiazdowych .
Tak jak (niezdegenerowane) wielokąty gwiezdne (które mają gęstość wielokątów większą niż 1) odpowiadają okrągłym wielokątom z nakładającymi się kafelkami , wielościany gwiezdne, które nie przechodzą przez środek, mają gęstość wielościanów większą niż 1 i odpowiadają kulistym wielościanom z nakładającymi się kafelkami; istnieje 47 niepryzmatycznych takich jednorodnych wielościanów gwiazd. Pozostałe 10 niepryzmatycznych jednorodnych wielościanów gwiezdnych, które przechodzą przez środek, to hemiwielościany, a także potwór Millera i nie mają dobrze zdefiniowanych gęstości.
Niewypukłe formy są zbudowane z trójkątów Schwarza .
Wszystkie jednolite wielościany są wymienione poniżej według ich grup symetrii i podzielone na podgrupy według ich rozmieszczenia wierzchołków.
Regularne wielościany są oznaczone ich symbolem Schläfli . Inne nieregularne jednolite wielościany są wymienione wraz z ich konfiguracją wierzchołków .
Dodatkowa figura, pseudowielki ośmiościan rombowy , zwykle nie jest uwzględniana jako prawdziwie jednorodna gwiazda polytope, mimo że składa się z regularnych ścian i ma te same wierzchołki.
Uwaga: Dla form niewypukłych poniżej dodatkowy deskryptor nonuniform jest używany, gdy układ wierzchołków kadłuba wypukłego ma taką samą topologię jak jedna z nich, ale ma nieregularne ściany. Na przykład niejednolita kantelowana forma może mieć prostokąty utworzone zamiast krawędzi zamiast kwadratów .
Symetria dwuścienna
Zobacz pryzmatyczny jednolity wielościan .
Symetria czworościenna
Istnieje jedna forma niewypukła, czworościan sześcienny , który ma symetrię czworościenną (z podstawową domeną trójkąta Möbiusa (3 3 2)).
Istnieją dwa trójkąty Schwarza , które generują unikalne niewypukłe jednolite wielościany: jeden trójkąt prostokątny ( 3 / 2 3 2) i jeden trójkąt ogólny ( 3 / 2 3 3). Ogólny trójkąt ( 3 ⁄ 2 3 3) generuje ośmiościan , który jest podany dalej z pełną symetrią ośmiościenną .
|
Układ wierzchołków ( kadłub wypukły ) |
Formy niewypukłe | |
|---|---|---|
 Czworościan |
||
 Rektyfikowany czworościan Ośmiościan |
 4. 3 ⁄ 2 .4.3 3 ⁄ 2 3 | 2 |
|
 Czworościan ścięty |
||
 Czworościan kantelowany ( Ośmiościan ośmiościan ) |
||
 Czworościan wielościenny ( Ośmiościan ścięty ) |
||
 Czworościan zadaszony ( Dwudziestościan ) |
||
Symetria ośmiościenna
Istnieje 8 form wypukłych i 10 form niewypukłych z symetrią ośmiościenną (z podstawową domeną trójkąta Möbiusa (4 3 2)).
Istnieją cztery trójkąty Schwarza , które generują formy niewypukłe, dwa trójkąty prostokątne ( 3 / 2 4 2) i ( 4 / 3 3 2) oraz dwa trójkąty ogólne: ( 4 / 3 4 3), ( 3 / 2 4 4) .
|
Układ wierzchołków ( kadłub wypukły ) |
Formy niewypukłe | ||
|---|---|---|---|
 Sześcian |
|||
 ośmiościan |
|||
 sześcienny ośmiościan |
 6. 4 ⁄ 3 .6.4 4 ⁄ 3 4 | 3 |
 6. 3 ⁄ 2 .6.3 3 ⁄ 2 3 | 3 |
|
 Ścięty sześcian |
 4. 8 / 3 . 4 / 3 . 8 / 5 2 4 / 3 ( 3 / 2 4 / 2 ) | |
 8 / 3 .3. 8 / 3 .4 3 4 | 4 / 3 |
 4. 3 ⁄ 2 .4.4 3 ⁄ 2 4 | 2 |
 Ścięty ośmiościan |
|||
 ośmiościan rombowy |
 4.8. 4 / 3 .8 2 4 ( 3 / 2 4 / 2 ) | |
 8. 3 ⁄ 2 0,8,4 3 ⁄ 2 4 | 4 |
 8 / 3 . 8 / 3 .3 2 3 | 4 / 3 |
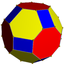 Niejednorodny ścięty ośmiościan sześcienny |
 4.6. 8 / 3 2 3 4 / 3 | |
||
 Niejednorodny ścięty ośmiościan sześcienny |
 8 / 3 0,6,8 3 4 4 / 3 | |
||
 Snub sześcian |
|||
Dwudziestościenna symetria
Istnieje 8 form wypukłych i 46 form niewypukłych o symetrii dwudziestościennej (z podstawową domeną trójkąta Möbiusa (5 3 2)). (lub 47 niewypukłych form, jeśli uwzględniono figurę Skillinga). Niektóre z niewypukłych form zadartych mają odblaskową symetrię wierzchołków.
Zdegenerowane przypadki
Coxeter zidentyfikował szereg zdegenerowanych wielościanów gwiazd metodą konstrukcyjną Wythoffa, które zawierają nakładające się krawędzie lub wierzchołki. Te zdegenerowane formy obejmują:
- Mały złożony dwudziestościan
- Wielki złożony dwudziestościan
- Mały złożony rombicosidodecahedron
- Wielki kompleks rombicosidodecahedron
- Złożony rombidodekadodecahedron
postać Skillinga
Kolejnym niewypukłym zdegenerowanym wielościanem jest dirhombidodecahedron wielki disnub , znany również jako figura Skillinga , który jest jednolity w wierzchołkach, ale ma pary krawędzi, które pokrywają się w przestrzeni, tak że cztery ściany spotykają się na niektórych krawędziach. Jest liczony jako zdegenerowany jednolity wielościan, a nie jednolity wielościan ze względu na podwójne krawędzie. Ma Ih .
Zobacz też
- Gwiazda wielokąta
- Lista jednolitych wielościanów
- Lista jednolitych wielościanów według trójkąta Schwarza
- Coxeter, HSM (13 maja 1954). „Jednolite wielościany”. Transakcje filozoficzne Royal Society of London. Seria A, nauki matematyczne i fizyczne . 246 (916): 401–450. doi : 10.1098/rsta.1954.0003 .
- Wenninger, Magnus (1974). Modele wielościanów . Wydawnictwo Uniwersytetu Cambridge. ISBN 0-521-09859-9 . OCLC 1738087 .
- Brückner, M. Vielecke und vielflache. Teoria und geschichte. . Lipsk, Niemcy: Teubner, 1900. [1]
- Sopow, SP (1970), „Dowód kompletności na liście elementarnych jednorodnych wielościanów”, Ukrainskiui Geometricheskiui Sbornik (8): 139–156, MR 0326550
- Skilling, J. (1975), „Kompletny zestaw jednolitych wielościanów”, Philosophical Transactions of the Royal Society of London. Seria A. Nauki matematyczne i fizyczne , 278 : 111–135, doi : 10.1098/rsta.1975.0022 , ISSN 0080-4614 , JSTOR 74475 , MR 0365333
- Har'El, Z. Jednolite rozwiązanie dla jednolitych wielościanów. , Geometriae Dedicata 47, 57-110, 1993. Zvi Har'El , Oprogramowanie Kaleido , Obrazy , obrazy podwójne
- Mäder, RE Uniform Polyhedra. Mathematica J. 3, 48-57, 1993. [2]
- Messer, Peter W. Wyrażenia w formie zamkniętej dla jednolitych wielościanów i ich liczb podwójnych. , Discrete & Computational Geometry 27:353-375 (2002).
- Klitzing, Richard. „Jednolite wielościany 3D” .