Mały ośmiościan sześcienny
| Mały ośmiościan sześcienny | |
|---|---|
|
|
| Typ | Jednolity wielościan gwiazdy |
| Elementy |
F = 20, E = 48 V = 24 (χ = −4) |
| Twarze po bokach | 8{3}+6{4}+6{8} |
| Diagram Coxetera |
|
| Symbol Wythoffa |
3/2 4 | 4 3 4/3 | 4 |
| Grupa symetrii | O h , [4,3], *432 |
| Odnośniki do indeksu | U 13 , C 38 , W 69 |
| Podwójny wielościan | Mały heksakronowy icositetrahedron |
| figura wierzchołka |
 4,8,3/2,8 |
| skrót Bowersa | Socco |
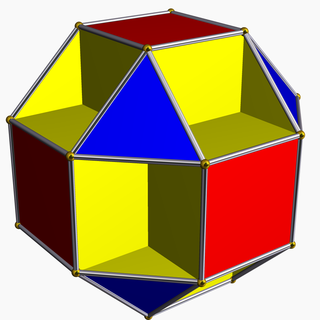
W geometrii mały sześcienny ośmiościan jest jednolitym wielościanem gwiazdy , indeksowanym jako U 13 . Ma 20 ścian (8 trójkątów , 6 kwadratów i 6 ośmiokątów ), 48 krawędzi i 24 wierzchołki. Jego figura wierzchołka jest skrzyżowanym czworobokiem .
Mały ośmiościan sześcienny jest fasetką ośmiościanu rombu . Jego ściany kwadratowe i ośmiokątne są równoległe do ścian sześcianu , podczas gdy ściany trójkątne są równoległe do ścian ośmiościanu : stąd nazwa sześcian-ośmiościan . Mały przyrostek służy do odróżnienia go od wielkiego sześciennego ośmiościanu , który ma również twarze we wspomnianych kierunkach.
Powiązane wielościany
Dzieli swój układ wierzchołków z gwiaździstym ściętym sześciościanem . Dodatkowo ma taki sam układ krawędzi jak ośmiościan rombowy (mający wspólne trójkątne ściany i 6 kwadratowych ścian) oraz mały romboheksościan (mający wspólne ośmiokątne ściany).
 ośmiościan rombowy |
 Mały ośmiościan sześcienny |
 Mały rombsześcian |
 Gwiaździsty ścięty sześciościan |
Powiązane płytki
Jak sugeruje charakterystyka Eulera, mały sześcienny ośmiościan jest toroidalnym wielościanem rodzaju 3 (topologicznie jest to powierzchnia rodzaju 3), a zatem może być interpretowany jako (wielościenne) zanurzenie wielościanu rodzaju 3, w dopełnieniu jego 24 wierzchołki, w 3-przestrzeni. (Okolica dowolnego wierzchołka jest topologicznie stożkiem na figurze ósemki, co nie może wystąpić w zanurzeniu. Należy zauważyć, że odniesienie Richtera pomija ten fakt.) Podstawowy wielościan (ignorując samoprzecięcia) definiuje jednolite ułożenie płytek tej powierzchni, więc mały sześcienny ośmiościan jest jednolitym wielościanem. W języku abstract polytopes , mały sześcienny ośmiościan jest wierną realizacją tego abstrakcyjnego toroidalnego wielościanu, co oznacza, że jest to niezdegenerowany wielościan i że mają tę samą grupę symetrii. W rzeczywistości każdy automorfizm abstrakcyjnej powierzchni rodzaju 3 z tym kafelkiem jest realizowany przez izometrię przestrzeni euklidesowej.
Powierzchnie wyższego rodzaju (rodzaj 2 lub wyższy) dopuszczają metrykę ujemnej stałej krzywizny (na mocy twierdzenia o uniformizacji ), a uniwersalnym pokryciem wynikowej powierzchni Riemanna jest płaszczyzna hiperboliczna . Odpowiednie ułożenie płaszczyzny hiperbolicznej ma wierzchołek na rysunku 3.8.4.8 (trójkąt, ośmiokąt, kwadrat, ośmiokąt). Jeśli powierzchni zostanie nadana odpowiednia metryka krzywizny = −1, pokrywająca mapa jest lokalną izometrią , a zatem abstrakcyjną figurą wierzchołka Jest taki sam. To ułożenie można oznaczyć symbolem Wythoffa 3 4 | 4 i jest przedstawiony po prawej stronie.

Alternatywnie i bardziej subtelnie, dzieląc każdą kwadratową ścianę na 2 trójkąty i każdą ośmiokątną na 6 trójkątów, mały ośmiościan sześcienny można zinterpretować jako nieregularne zabarwienie kombinatorycznie regularnych (nie tylko jednolitych ) płytek powierzchni rodzaju 3 przez 56 trójkątów równobocznych, spotykających się w 24 wierzchołkach, każdy o stopniu 7. To regularne kafelkowanie jest znaczące, ponieważ jest to kafelkowanie kwarcu Kleina , powierzchnia rodzaju 3 o najbardziej symetrycznej metryce (automorfizmy tego kafelkowania równe izometrii powierzchni), a grupa automorfizmów tej powierzchni zachowująca orientację jest izomorficzna z rzutową specjalną grupą liniową PSL (2,7), równoważnie GL ( 3,2) (grupa rzędu 168 wszystkich izometrii zachowujących orientację). Zauważ, że mały sześcienny ośmiościan nie jest realizacja tego abstrakcyjnego wielościanu, ponieważ ma on tylko 24 symetrie zachowujące orientację (nie każdy abstrakcyjny automorfizm jest realizowany przez izometrię euklidesową) - izometrie małego ośmiościanu sześciennego zachowują nie tylko trójkątne płytki, ale także kolorystykę, a zatem są właściwa podgrupa grupy pełnej izometrii.
Odpowiednie ułożenie płaszczyzny hiperbolicznej (pokrycie uniwersalne) to ułożenie trójkątne rzędu 7 . Grupę automorfizmów kwarcu Kleina można rozszerzyć (o symetrię, której nie realizuje symetria wielościanu, a mianowicie „zamiana dwóch punktów końcowych krawędzi przecinających kwadraty i ośmiościany) w celu uzyskania grupy Mathieu M 24 ” .
Zobacz też
- Richter, David A., How to Make the Mathieu Group M 24 , dostęp 2010-04-15

