Lista modeli wielościanów Wenningera

To jest indeksowana lista jednolitych i gwiaździstych wielościanów z książki Polyhedron Models autorstwa Magnusa Wenningera .

Książka została napisana jako przewodnik po budowaniu wielościanów jako modeli fizycznych. Zawiera szablony elementów twarzy do budowy i pomocne wskazówki dotyczące budowania, a także krótkie opisy teorii stojącej za tymi kształtami. Zawiera 75 niepryzmatycznych jednolitych wielościanów , a także 44 gwiaździste formy wypukłych regularnych i quasiregularnych wielościanów.

Wymienione tutaj modele mogą być cytowane jako „numer modelu Wenninger N ” lub W _N dla zwięzłości.

Wielościany są pogrupowane w 5 tabelach: regularne (1–5), półregularne (6–18), regularne wielościany gwiazd (20–22,41), stellacje i związki (19–66) oraz jednolite wielościany gwiazd (67–119 ). Cztery regularne wielościany gwiazd są wymienione dwukrotnie, ponieważ należą zarówno do jednolitych wielościanów, jak i do grup gwiaździstych.

Bryły platońskie (regularne wypukłe wielościany) W1 do W5

Indeks	Nazwa	Zdjęcie	Podwójna nazwa	Podwójny obraz	Symbol Wythoffa	Figura wierzchołka i symbol Schläfliego	Grupa symetrii	U #	K#	V	mi	F	Twarze według typu
1	Czworościan		Czworościan		3|2 3	{3,3}	T d	U01	K06	4	6	4	4{3}
2	Oktaedr		Prostopadłościan		4|2 3	{3,4}	O godz	U05	K10	6	12	8	8{3}
3	Sześcian (sześcian)		Oktaedr		3|2 4	{4,3}	O godz	U06	K11	8	12	6	6{4}
4	dwudziestościan		Dwunastościan		5|2 3	{3,5}	ja godz	U22	K27	12	30	20	20{3}
5	Dwunastościan		dwudziestościan		3|2 5	{5,3}	ja godz	U23	K28	20	30	12	12{5}

Bryły Archimedesa (półregularne) W6 do W18

Indeks	Nazwa	Zdjęcie	Podwójna nazwa	Podwójny obraz	Symbol Wythoffa	figura wierzchołka	Grupa symetrii	U #	K#	V	mi	F	Twarze według typu
6	Ścięty czworościan		czworościan triakisa		2 3|3	3.6.6	T d	U02	K07	12	18	8	4{3} + 4{6}
7	Ścięty ośmiościan		sześciościan tetrakisa		2 4|3	4.6.6	O godz	U08	K13	14	36	24	6{4} + 8{6}
8	Ścięty sześcian		ośmiościan triaki		2 3|4	3.8.8	O godz	U09	K14	24	36	14	8{3} + 6{8}
9	Dwudziestościan ścięty		pentakisowy dwunastościan		2 5|3	5.6.6	ja godz	U25	K30	60	90	32	12{5} + 20{6}
10	Dwunastościan ścięty		dwudziestościan triakis		2 3|5	3.10.10	ja godz	U26	K31	60	90	32	20{3} + 12{10}
11	sześcienny ośmiościan		dwunastościan rombowy		2|3 4	3.4.3.4	O godz	U07	K12	12	24	14	8{3} + 6{4}
12	dwudziestościan		rombowy triakontaedr		2|3 5	3.5.3.5	ja godz	U24	K29	30	60	32	20{3} + 12{5}
13	Mały ośmiościan rombowy		icositetrahedron naramienny		3 4|2	3.4.4.4	O godz	U10	K15	24	48	26	8{3}+(6+12){4}
14	Mały dziesięciościan rombowy		sześciokąt naramienny		3 5|2	3.4.5.4	ja godz	U27	K32	60	120	62	20{3} + 30{4} + 12{5}
15	Ścięty ośmiościan ośmiościan (wielki ośmiościan rombowy)		disdyakis dwunastościan		2 3 4|	4.6.8	O godz	U11	K16	48	72	26	12{4} + 8{6} + 6{8}
16	Dwudziestościan ścięty (Wielki rombicosidodekahedron)		disdyakis triacontahedron		2 3 5|	4.6.10	ja godz	U28	K33	120	180	62	30{4} + 20{6} + 12{10}
17	Snub sześcian		pięciokątny icositetrahedron		|2 3 4	3.3.3.3.4	O	U12	K17	24	60	38	(8 + 24){3} + 6{4}
18	Zadarty dwunastościan		sześciokąt pięciokątny		|2 3 5	3.3.3.3.5	I	U29	K34	60	150	92	(20 + 60){3} + 12{5}

Wielościany Keplera – Poinsota ( wielościany gwiazdy regularnej ) W20, W21, W22 i W41

Indeks	Nazwa	Zdjęcie	Podwójna nazwa	Podwójny obraz	Symbol Wythoffa	Figura wierzchołka i symbol Schläfliego	Grupa symetrii	U #	K#	V	mi	F	Twarze według typu
20	Mały dwunastościan gwiaździsty		Wielki dwunastościan		5|2 5 / 2	{ 5 / 2 ,5}	ja godz	U34	K39	12	30	12	12 { 5 / 2 }
21	Wielki dwunastościan		Mały dwunastościan gwiaździsty		5 / 2 |2 5	{5, 5 / 2 }	ja godz	U35	K40	12	30	12	12{5}
22	Wielki gwiaździsty dwunastościan		Wielki dwudziestościan		3|2 5 / 2	{ 5 / 2 ,3}	ja godz	U52	K57	20	30	12	12 { 5 / 2 }
41	Wielki dwudziestościan (16. gwiazda dwudziestościanu)		Wielki gwiaździsty dwunastościan		5 / 2 |2 3	{3, 5 / 2 }	ja godz	U53	K58	12	30	20	20{3}

Stellacje: modele od W19 do W66

Stellacje ośmiościanu

Indeks	Nazwa	Grupa symetrii	Zdjęcie	aspekty
2	Ośmiościan (zwykły)	O godz
19	Ośmiościan gwiaździsty (złożenie dwóch czworościanów)	O godz

Stelacje dwunastościanu

Indeks	Nazwa	Grupa symetrii	Zdjęcie	aspekty
5	dwunastościan (zwykły)	ja godz
20	Mały dwunastościan gwiaździsty (zwykły) (pierwsza gwiazda dwunastościanu)	ja godz
21	Wielki dwunastościan (regularny) (druga gwiazda dwunastościanu)	ja godz
22	Wielki dwunastościan gwiaździsty (regularny) (trzecia gwiazda dwunastościanu)	ja godz

Stelacje dwudziestościanu

Indeks	Nazwa	Grupa symetrii	Zdjęcie	aspekty
4	Dwudziestościan (zwykły)	ja godz
23	Związek pięciu ośmiościanów (pierwsza złożona gwiazda dwudziestościanu)	ja godz
24	Związek pięciu czworościanów (druga złożona gwiazda dwudziestościanu)	I
25	Związek dziesięciu czworościanów (trzecia złożona gwiazda dwudziestościanu)	ja godz
26	Mały triambiczny dwudziestościan (pierwsza stelacja dwudziestościanu) ( Triakis dwudziestościan )	ja godz
27	Druga gwiazda dwudziestościanu	ja godz
28	Wykopany dwunastościan (trzecia gwiazda dwudziestościanu)	ja godz
29	Czwarta gwiazda dwudziestościanu	ja godz
30	Piąta gwiazda dwudziestościanu	ja godz
31	Szósta gwiazda dwudziestościanu	ja godz
32	Siódma gwiazda dwudziestościanu	ja godz
33	Ósma gwiazda dwudziestościanu	ja godz
34	Dziewiąta gwiazda dwudziestościanu Wielki triambiczny dwudziestościan	ja godz
35	Dziesiąta gwiazda dwudziestościanu	I
36	Jedenasta gwiazda dwudziestościanu	I
37	Dwunasta gwiazda dwudziestościanu	ja godz
38	Trzynasta stelacja dwudziestościanu	I
39	Czternasta stelacja dwudziestościanu	I
40	Piętnasta stelacja dwudziestościanu	I
41	Wielki dwudziestościan (regularny) (szesnasta gwiazda dwudziestościanu)	ja godz
42	Końcowa stellacja dwudziestościanu	ja godz

Stellacje sześciennego ośmiościanu

Indeks	Nazwa	Grupa symetrii	Zdjęcie	Fasety (płaszczyzny ośmiościenne)	Fasety (płaszczyzny sześcianu)
11	Sześcienny ośmiościan (zwykły)	O godz
43	Związek sześcianu i ośmiościanu (pierwsza gwiazda ośmiościanu sześciennego)	O godz
44	Druga gwiazda sześciennego ośmiościanu	O godz
45	Trzecia gwiazda sześciennego ośmiościanu	O godz
46	Czwarta gwiazda sześciennego ośmiościanu	O godz

Stelacje dwudziestościanu

Indeks	Nazwa	Grupa symetrii	Zdjęcie	Fasetki (płaszczyzny dwudziestościenne)	Fasetki (płaszczyzny dwunastościenne)
12	Dwudziestościan (regularny)	ja godz
47	(Pierwsza stelacja dwudziestościanu) Związek dwunastościanu i dwudziestościanu	ja godz
48	Druga stellacja dwudziestościanu	ja godz
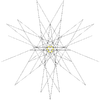
49	Trzecia gwiazda dwudziestościanu	ja godz
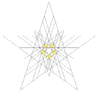
50	Czwarta stelacja dwudziestościanu (związek małego dwunastościanu gwiaździstego i dwudziestościanu triakis)	ja godz
51	Piąta gwiazda dwudziestościanu (związek małego dwunastościanu gwiaździstego i pięciu ośmiościanów)	ja godz
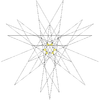
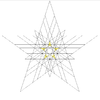
52	Szósta gwiazda dwudziestościanu	ja godz
53	Siódma stelacja dwudziestościanu	ja godz
54	Ósma gwiazda dwudziestościanu (związek pięciu czworościanów i dwunastościanu wielkiego)	I
55	Dziewiąta gwiazda dwudziestościanu	ja godz
56	Dziesiąta gwiazda dwudziestościanu	ja godz
57	Jedenasta stelacja dwudziestościanu	ja godz
58	Dwunasta stelacja dwudziestościanu	ja godz
59	Trzynasta stelacja dwudziestościanu	ja godz
60	Czternasta stelacja dwudziestościanu	ja godz
61	Związek dwunastościanu wielkiego gwiaździstego i dwudziestościanu wielkiego	ja godz
62	Piętnasta stelacja dwudziestościanu	ja godz
63	Szesnasta stelacja dwudziestościanu	ja godz
64	Siedemnasta stelacja dwudziestościanu	ja godz
65	Osiemnasta stelacja dwudziestościanu	ja godz
66	Dziewiętnasta stelacja dwudziestościanu	ja godz

Jednorodne niewypukłe bryły W67 do W119

Indeks	Nazwa	Zdjęcie	Podwójna nazwa	Podwójny obraz	Symbol Wythoffa	figura wierzchołka	Grupa symetrii	U #	K#	V	mi	F	Twarze według typu
67	czworościan		Tetrahemiheksakron		3 / 2 3|2	4. 3 / 2 .4.3	T d	U04	K09	6	12	7	4{3}+3{4}
68	ośmiościan		oktahemioktakron		3 / 2 3|3	6. 3 / 2 .6.3	O godz	U03	K08	12	24	12	8{3}+4{6}
69	Mały ośmiościan sześcienny		Mały heksakronowy icositetrahedron		3 / 2 4|4	8.3 / 2.8.4 _ _	O godz	U13	K18	24	48	20	8{3}+6{4}+6{8}
70	Mały dwudziestościan dwutrygonalny		Mały dwudziestościan triambiczny		3| 5 / 2 3	( 5 / 2 .3) 3	ja godz	U30	K35	20	60	32	20{3}+12{ 5 / 2 }
71	Mały icosicosidodecahedron		Mały dwudziestościan sześciokątny		5 / 2 3|3	6. 5 / 2 .6.3	ja godz	U31	K36	60	120	52	20{3}+12{ 5 / 2 }+20{6}
72	Mały dwunastościan dwunastościanu		Mały dwunastościan sześciokątny		3 / 2 5|5	10.3 / 2 .10.5 _	ja godz	U33	K38	60	120	44	20{3}+12{5}+12{10}
73	dwunastościan		Przyśrodkowy triacontahedron rombowy		2| 5 / 2 5	( 5 / 2,5 ) 2	ja godz	U36	K41	30	60	24	12{5}+12{ 5 / 2 }
74	Mały rombidodecahedron		Mały rombidodekaron		2 5 / 2 5|	10.4. 10 / 9 . 4 / 3	ja godz	U39	K44	60	120	42	30{4}+12{10}
75	Ścięty dwunastościan wielki		Mały dwunastościan stellapentakis		2 5 / 2 |5	10.10. 5 / 2	ja godz	U37	K42	60	90	24	12{ 5 / 2 }+12{10}
76	Rombidodekadodziesięciościan		Sześciokąt naramienny przyśrodkowy		5 / 2 5|2	4. 5 / 2 .4.5	ja godz	U38	K43	60	120	54	30{4}+12{5}+12{ 5 / 2 }
77	Wielki sześcienny ośmiościan		Wielki heksakronowy icositetrahedron		3 4| 4 / 3	8 / 3 .3. 8 / 3 .4	O godz	U14	K19	24	48	20	8{3}+6{4}+6{ 8 / 3 }
78	Sześcian hemiośmiościan		heksahemioktakron		4 / 3 4|3	6. 4 / 3 .6.4	O godz	U15	K20	12	24	10	6{4}+4{6}
79	Cubitruncated cuboctahedron (Cuboctatruncated cuboctahedron)		Sześcian Tetradyakisa		4 / 3 3 4|	8 / 3 .6.8	O godz	U16	K21	48	72	20	8{6}+6{8}+6{ 8 / 3 }
80	Ditrygonalny dwunastościan		Przyśrodkowy dwudziestościan triambiczny		3| 5 / 3 5	( 5 / 3 , 5) 3	ja godz	U41	K46	20	60	24	12{5}+12{ 5 / 2 }
81	Wielki dwunastościan dwutrygonalny dwunastościan		Wielki dwutrygonalny dwunastościan sześciokątny		3 5| 5 / 3	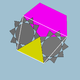10 / 3 .3. 10 / 3 .5	ja godz	U42	K47	60	120	44	20{3}+12{5}+12{ 10 / 3 }
82	Mały dwunastościan dwutrygonalny dwunastościan		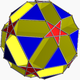Mały dwutrygonalny dwunastościan sześciokątny		5 / 3 3|5	10.5 / 3 .10.3 _	ja godz	U43	K48	60	120	44	20{3}+12{ 5 / 2 }+12{10}
83	Dwudziestościan dwunastościanu		Sześciokąt dwudziestościan przyśrodkowy		5 / 3 5|3	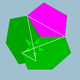6. 5 / 3 .6.5	ja godz	U44	K49	60	120	44	12{5}+12{ 5 / 2 }+20{6}
84	Icosidodecatruncated dwunastościan (Icosidodecatruncated dwudziestościan)		Dwudziestościan Tridyakisa		5 / 3 3 5|	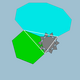10 / 3 .6.10	ja godz	U45	K50	120	180	44	20{6}+12{10}+12{ 10 / 3 }
85	Niewypukły wielki ośmiościan rombowy (Quasirhombicuboctahedron)		Wielki icositetrahedron naramienny		3 / 2 4|2	4. 3 / 2 .4.4	O godz	U17	K22	24	48	26	8{3}+(6+12){4}
86	Mały rombsześcian		Mały romboheksakron		3 / 2 2 4|	4.8. 4 / 3 .8	O godz	U18	K23	24	48	18	12{4}+6{8}
87	Dwudziestościan dwutrygonalny wielki		Wielki dwudziestościan triambiczny		3 / 2 |3 5	(5.3.5.3.5.3)/ 2	ja godz	U47	K52	20	60	32	20{3}+12{5}
88	Wielki icosicosidodecahedron		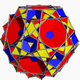Wielki dwudziestościan sześciokątny		3 / 2 5|3	6. 3 / 2 .6.5	ja godz	U48	K53	60	120	52	20{3}+12{5}+20{6}
89	Mały icosihemidodecahedron		Mały icosihemidodecacron		3 / 2 3|5	10.3 / 2 .10.3 _	ja godz	U49	K54	30	60	26	20{3}+6{10}
90	Mały dwunastościan		Mały dodecykozaron		3 / 2 3 5|	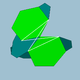10.6. 10 / 9 . 6 / 5	ja godz	U50	K55	60	120	32	20{6}+12{10}
91	Mały dwunastościan hemidodecahedron		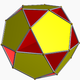Mały dodekahemidodekakron		5 / 4 5|5	10. 5 / 4 .10.5	ja godz	U51	K56	30	60	18	12{5}+6{10}
92	Sześcian ścięty gwiaździsty (sześcian quasi ścięty)		Wielki ośmiościan triaki		2 3| 4 / 3	8 / 3 . 8 / 3 .3	O godz	U19	K24	24	36	14	8{3}+6{ 8 / 3 }
93	Wielki ścięty ośmiościan sześcienny (Quasitruncated cuboctahedron)		Wielki dwunastościan disdyaki		4 / 3 2 3|	8 / 3 .4.6	O godz	U20	K25	48	72	26	12{4}+8{6}+6{ 8 / 3 }
94	Wielki dwudziestościan		Wielki rombowy triakontaedr		2| 5 / 2 3	( 5 / 2 .3) 2	ja godz	U54	K59	30	60	32	20{3}+12{ 5 / 2 }
95	Ścięty wielki dwudziestościan		Wielki dwunastościan stellapentakis		2 5 / 2 |3	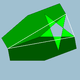6.6. 5 / 2	ja godz	U55	K60	60	90	32	12{ 5 / 2 }+20{6}
96	romboidalny		Rombikosakron		2 5 / 2 3|	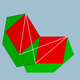6.4. 6 / 5 . 4 / 3	ja godz	U56	K61	60	120	50	30{4}+20{6}
97	Mały gwiaździsty dwunastościan ścięty (Quasitruncated mały dwunastościan gwiaździsty)		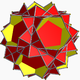Wielki dwunastościan pentakisa		2 5| 5 / 3	10 / 3 . 10 / 3 .5	ja godz	U58	K63	60	90	24	12{5}+12{ 10 / 3 }
98	Dwunastościan ścięty (Quasitruncated dwunastościan)		Przyśrodkowy triacontahedron disdyakis		5 / 3 2 5|	10 / 3 .4.10	ja godz	U59	K64	120	180	54	30{4}+12{10}+12{ 10 / 3 }
99	Wielki dwunastościan dwunastościanu		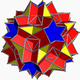Wielki dwunastościan sześciokątny		5 / 2 3| 5 / 3	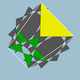10 / 3 . 5 / 2 . 10 / 3 .3	ja godz	U61	K66	60	120	44	20 {3} +12 { 5/2 }+12 { 10/3 }
100	Mały dodecahemicosahedron		Mały dodecahemicosacron		5 / 3 5 / 2 |3	6. 5 / 3 .6. 5 / 2	ja godz	U62	K67	30	60	22	12{ 5 / 2 }+10{6}
101	Wielki dwunastościan		Wielki dodecykozaron		5 / 3 5 / 2 3|	6. 10 / 3 . 6 / 5 . 10 / 7	ja godz	U63	K68	60	120	32	20{6}+12{ 10 / 3 }
102	Wielki dwunastościan		Wielki dodecahemicosacron		5 / 4 5|3	6. 5 / 4 .6.5	ja godz	U65	K70	30	60	22	12{5}+10{6}
103	Wielki rombsześcian		Wielki romboheksakron		4 / 3 3 / 2 2|	4. 8 / 3 . 4 / 3 . 8 / 5	O godz	U21	K26	24	48	18	12{4}+6{ 8 / 3 }
104	Wielki gwiaździsty dwunastościan ścięty (Quasitruncated wielki dwunastościan gwiaździsty)		Wielki dwudziestościan triakis		2 3| 5 / 3	10 / 3 . 10 / 3 .3	ja godz	U66	K71	60	90	32	20{3}+12{ 10 / 3 }
105	Niewypukły wielki rombosidodekahedron (Quasirhombicosidodecahedron)		Sześciokąt wielki naramienny		5 / 3 3|2	4. 5 / 3 .4.3	ja godz	U67	K72	60	120	62	20{3}+30{4}+12{ 5 / 2 }
106	Wielki icosihemidodecahedron		Wielki icosihemidodecacron		3 3| 5 / 3	10 / 3 . 3 / 2 . 10 / 3 .3	ja godz	U71	K76	30	60	26	20{3}+6{ 10 / 3 }
107	Wielki dwunastościan hemidodecahedron		Wielki dodekahemidodekakron		5 / 3 5 / 2 | 5 / 3	10 / 3 . 5 / 3 . 10 / 3 . 5 / 2	ja godz	U70	K75	30	60	18	12{ 5 / 2 } +6{ 10 / 3 }
108	Wielki dwudziestościan ścięty (Wielki quasiścięty dwudziestościan)		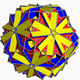Wielki disdyakis triacontahedron		5 / 3 2 3|	10 / 3 .4.6	ja godz	U68	K73	120	180	62	30{4}+20{6}+12{ 10 / 3 }
109	Wielki rombidodekaedr		Wielki rombidodekaron		3 / 2 5 / 3 2|	4. 10 / 3 . 4 / 3 . 10 / 7	ja godz	U73	K78	60	120	42	30{4}+12{ 10 / 3 }
110	Mały zadarty icosicosidodecahedron		Mały sześciokątny sześcian		| 5 / 2 3 3	3.3.3.3.3. 5 / 2	ja godz	U32	K37	60	180	112	(40+60){3}+12{ 5 / 2 }
111	Zadarty dwunastościan		Przyśrodkowy pięciokątny sześciokątny		|2 5 / 2 5	3.3. 5 / 2 .3.5	I	U40	K45	60	150	84	60{3}+12{5}+12{ 5 / 2 }
112	Zadarty dwudziestościan dwunastościanu		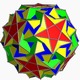Przyśrodkowy sześciokątny sześcian		| 5 / 3 3 5	3.3.3.3.5. 5 / 3	I	U46	K51	60	180	104	(20+6){3}+12{5}+12{ 5 / 2 }
113	Wielki odwrócony zadarty dwudziestościan		Wielki odwrócony pięciokątny sześciokąt		| 5 / 3 2 3	3.3.3.3. 5 / 3	I	U69	K74	60	150	92	(20+60){3}+12{ 5 / 2 }
114	Odwrócony zadarty dwunastościan		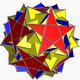Przyśrodkowy odwrócony pięciokątny sześciokąt		| 5 / 3 2 5	3. 5 / 3 .3.3.5	I	U60	K65	60	150	84	60{3}+12{5}+12{ 5 / 2 }
115	Wielki afront dodecicosidodecahedron		Wielki sześciokąt sześciokątny		| 5 / 3 5 / 2 3	3. 5 / 3 .3. 5 / 2 .3.3	I	U64	K69	60	180	104	(20+60){3}+(12+12){ 5 / 2 }
116	Wielki zadarty dwudziestościan		Wielki pięciokątny sześciokąt		|2 5 / 2 5 / 2	3.3.3.3. 5 / 2	I	U57	K62	60	150	92	(20+60){3}+12{ 5 / 2 }
117	Wielki retrosnub dwudziestościan		Wielki pentagramowy heksekontaedr		| 3 / 2 5 / 3 2	(3.3.3.3. 5 / 2 )/ 2	I	U74	K79	60	150	92	(20+60){3}+12{ 5 / 2 }
118	Mały retrosnub icosicosidodecahedron		Mały sześciokąt heksagramowy		| 3 / 2 3 / 2 5 / 2	(3.3.3.3.3. 5 / 2 )/ 2	ja godz	U72	K77	180	60	112	(40+60){3}+12{ 5 / 2 }
119	Wielki dirhombicosidodecahedron		Wielki dirhombicosidodecacron		| 3 / 2 5 / 3 3 5 / 2	(4.5 / 3 .4.3.4 . 5 / 2 .4. 3 / 2 )/ 2	ja godz	U75	K80	60	240	124	40{3}+60{4}+24{ 5 / 2 }

powrót do góry

Zobacz też

• Lista jednolitych wielościanów
• Pięćdziesiąt dziewięć dwudziestościanów
• Lista stelacji wielościennych

•   Wenninger, Magnus (1974). Modele wielościanów . Wydawnictwo Uniwersytetu Cambridge. ISBN 0-521-09859-9 .
  • Errata
    • W Wenninger figura wierzchołka dla W90 jest błędnie pokazana jako mająca równoległe krawędzie.
•   Wenninger, Magnus (1979). Modele sferyczne . Wydawnictwo Uniwersytetu Cambridge. ISBN 0-521-29432-0 .

Linki zewnętrzne

• Magnusa J. Wenningera
• Oprogramowanie użyte do generowania obrazów w tym artykule:
  • Stella: Polyhedron Navigator Stella (oprogramowanie) - Może tworzyć i drukować siatki dla wszystkich modeli wielościanów Wenningera.
  • Aplet stelacji wielościanów Władimira Bułatowa
  • Aplet Polyhedra Stellations Vladimira Bulatova w pakiecie jako aplikacja OS X
• M. Wenninger, Polyhedron Models , Errata : znane błędy w różnych wydaniach.