Końcowa stellacja dwudziestościanu

Końcowa stellacja dwudziestościanu
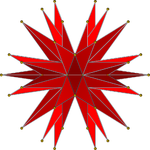Dwa symetryczne rzuty prostopadłe
Grupa symetrii	dwudziestościan ( I h )
Typ	Dwudziestościan gwiaździsty , 8. z 59
Symbolika	Du Val H Wenninger : W 42
Elementy (jako wielościan gwiazdy)	F = 20, E = 90 V = 60 ( χ = −10)
Elementy (jako prosty wielościan)	F = 180, E = 270, V = 92 ( χ = 2)
Właściwości (jako wielościan gwiazdy)	Wierzchołek-przechodnie , twarz-przechodnie
Diagram stellacyjny Rdzeń stellacyjny Wypukły kadłub dwudziestościan dwudziestościan ścięty

W geometrii kompletna lub ostateczna stelacja dwudziestościanu jest najbardziej zewnętrzną stelacją dwudziestościanu i jest „kompletna” i „ostateczna” , ponieważ obejmuje wszystkie komórki na diagramie stelacyjnym dwudziestościanu . Oznacza to, że każde trzy przecinające się płaszczyzny dwudziestościanu rdzenia przecinają się albo na wierzchołku tego wielościanu, albo wewnątrz niego.

Ten wielościan jest siedemnastą stelacją dwudziestościanu i podany jako indeks modelu Wenningera 42 .

Jako figura geometryczna ma dwie interpretacje, opisane poniżej:

• Jako nieregularna gwiazda (samoprzecinająca się) wielościan z 20 identycznymi samoprzecinającymi się ścianami enneagramicznymi , 90 krawędziami, 60 wierzchołkami.
• Jako prosty wielościan ze 180 trójkątnymi ścianami (60 równoramiennych, 120 skalnych), 270 krawędziami i 92 wierzchołkami. Ta interpretacja jest przydatna przy modelu wielościanu .

Johannes Kepler badał gwiezdne gwiazdy, które tworzą regularne wielościany gwiazd ( wielościany Keplera-Poinsota ) w 1619 r., ale kompletny dwudziestościan z nieregularnymi ścianami został po raz pierwszy zbadany w 1900 r. przez Maxa Brücknera .

Historia

Model Brücknera (Taf. XI, ryc. 14, 1900)

Kolczatka

• 1619: W Harmonices Mundi Johannes Kepler po raz pierwszy zastosował proces stellacji, uznając mały dwunastościan gwiaździsty i dwunastościan wielki gwiaździsty za regularne wielościany.
• 1809: Louis Poinsot ponownie odkrył wielościany Keplera i dwa kolejne, wielki dwudziestościan i dwunastościan wielki , jako wielościany regularnej gwiazdy, zwane obecnie wielościanami Keplera-Poinsota .
• 1812: Augustin-Louis Cauchy dokonał dalszego wyliczenia wielościanów gwiazd, udowadniając, że istnieją tylko 4 regularne wielościany gwiazd.
• 1900: Max Brückner rozszerzył teorię stelacji poza regularne formy i zidentyfikował dziesięć stelacji dwudziestościanu, w tym całą stelację .
• 1924: AH Wheeler w 1924 opublikował listę 20 form gwiaździstych (22 łącznie z kopiami odblaskowymi), w tym również pełną stellację .
• 1938: W swojej książce z 1938 roku The Fifty Nine Icosahedra , HSM Coxeter , P. Du Val , HT Flather i JF Petrie podali zestaw reguł stellacji dla dwudziestościanu regularnego i podali systematyczne wyliczenie pięćdziesięciu dziewięciu gwiazd, które są zgodne z tymi zasadami . Cała stelacja jest wymieniona jako ósma w książce.
• 1974: W książce Wenningera Polyhedron Models z 1974 r. , ostateczna gwiazda dwudziestościanu jest zawarta jako 17. model dwudziestościanu gwiaździstego o numerze indeksu W ₄₂ .
• 1995: Andrew Hume nazwał go w swojej wielościennej bazie danych Netlib echidnahedron ( echidna , czyli kolczasty mrówkojad to mały ssak pokryty szorstkimi włosami i kolcami , który zwija się w kłębek, aby się chronić).

Interpretacje

Schemat stellacyjny dwudziestościanu z ponumerowanymi komórkami. Cały dwudziestościan jest utworzony ze wszystkich komórek gwiaździstych, ale widoczne są tylko najbardziej zewnętrzne obszary, oznaczone na schemacie jako „13”.

Model 3D końcowej gwiazdy dwudziestościanu

Jako gwiazda

Główny artykuł: Pięćdziesiąt dziewięć dwudziestościanów

Stelacja wielościanu rozciąga ściany wielościanu na nieskończone płaszczyzny i generuje nowy wielościan, który jest ograniczony przez te płaszczyzny jako ściany i przecięcia tych płaszczyzn jako krawędzie . Fifty Nine Icosahedra wylicza gwiazdy dwudziestościanu foremnego , zgodnie z zestawem reguł przedstawionych przez JCP Millera , w tym pełną gwiazdę . Symbolem Du Val pełnej gwiaździstej jest H , ponieważ obejmuje wszystkie komórki na diagramie gwiaździstym aż do najbardziej zewnętrznej warstwy „h” włącznie.

Jako prosty wielościan

Model wielościenny można zbudować z 12 zestawów ścian, z których każdy składa się w grupę pięciu piramid.

Jako prosty, widoczny wielościan powierzchniowy, zewnętrzna forma ostatecznej stellacji składa się ze 180 trójkątnych ścian, które są najbardziej zewnętrznymi trójkątnymi obszarami na diagramie stellacji. Łączą się one wzdłuż 270 krawędzi, które z kolei spotykają się w 92 wierzchołkach, z charakterystyką Eulera równą 2.

92 wierzchołki leżą na powierzchniach trzech koncentrycznych sfer. Najbardziej wewnętrzna grupa 20 wierzchołków tworzy wierzchołki dwunastościanu foremnego; kolejna warstwa 12 tworzy wierzchołki dwudziestościanu foremnego; a zewnętrzna warstwa 60 tworzy wierzchołki niejednorodnego dwudziestościanu ściętego. Promienie tych sfer są w stosunku

${\ Displaystyle {\ sqrt {{\ Frac {3} {2}} \ lewo (3 + {\ sqrt {5}} \ prawej)}} \,: \, {\ sqrt {{\ frac {1} 2}}\left(25+11{\sqrt {5}}\right)}}\,:\,{\sqrt {{\frac {1}{2}}\left(97+43{\sqrt { 5}}\prawo)}}\,.}$

Wypukłe kadłuby każdej sfery wierzchołków

Wewnętrzny	Środek	Zewnętrzny	Wszystkie trzy
20 wierzchołków	12 wierzchołków	60 wierzchołków	92 wierzchołki
Dwunastościan	dwudziestościan	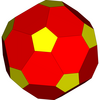Niejednolity dwudziestościan ścięty	Kompletny dwudziestościan

Rozważany jako trójwymiarowy obiekt bryłowy o długościach krawędzi a , φ a , φ ² a i φ ² a √ 2 (gdzie φ jest złotym podziałem ), cały dwudziestościan ma pole powierzchni

${\ Displaystyle S = {\ Frac {1} {20}} (13211 + {\ sqrt {174306161}}) a ^ {2} \,,}$

i głośność

${\ Displaystyle V = (210 + 90 {\ sqrt {5}}) a ^ {3} \,.}$

Jako gwiazda wielościanu

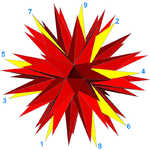Dwadzieścia 9 ⁄ 4 ścian wielokątnych (jedna ściana jest narysowana na żółto z oznaczonymi 9 wierzchołkami).

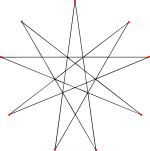2-izogonalne 9 / 4 ściany

Całą gwiazdę można również postrzegać jako samoprzecinający się wielościan gwiazdy mający 20 ścian odpowiadających 20 ścianom leżącego poniżej dwudziestościanu. Każda ściana jest nieregularnym wielokątem gwiazdowym 9/4 lub enneagramem . Ponieważ trzy ściany spotykają się w każdym wierzchołku, ma on 20 × 9 / 3 = 60 wierzchołków (są to najbardziej zewnętrzne warstwy widocznych wierzchołków i tworzą wierzchołki „kolców”) oraz 20 × 9 / 2 = 90 krawędzi (każda krawędź gwiezdny wielościan obejmuje i łączy dwie ze 180 widocznych krawędzi).

Traktowana jako dwudziestościan gwiazdy, cała gwiazda jest szlachetnym wielościanem , ponieważ jest zarówno izoedryczna (przechodnia ściany), jak i izogonalna (przechodnia wierzchołka).

Zobacz też

• Wielościan Keplera-Poinsota
• Lista modeli wielościanów Wenningera

Notatki

•   Brückner, Max (1900). Vielecke und Vielflache: Theorie und Geschichte . Lipsk: BG Treubner. ISBN 978-1-4181-6590-1 . (w języku niemieckim) WorldCat angielski: wielokąty i wielościany: teoria i historia . Fotografie modeli: Tafel VIII (tablica VIII) itp. Wysoka rozdzielczość. skany.
• AH Wheeler, Niektóre formy dwudziestościanu i metoda wyprowadzania i oznaczania wyższych wielościanów , Proc. Intern. Matematyka Kongres, Toronto, 1924, tom. 1, s. 701–708
•   HSM Coxeter , Regularne Polytopes , (wydanie trzecie, 1973), wydanie Dover, ISBN 0-486-61480-8 , 3,6 6,2 Stellating the Platonic solids , s. 96–104
•    Coxetera, Harolda Scotta MacDonalda ; Du Val, P.; Flather, HT; Petrie, JF (1999), The pięćdziesiąt dziewięć dwudziestościanów (wyd. 3), Tarquin, ISBN 978-1-899618-32-3 , MR 0676126 (1st Edn University of Toronto (1938))
•   Wenninger, Magnus J. , modele wielościanu ; Cambridge University Press, 1. wydanie (1983), Ppbk (2003). ISBN 978-0-521-09859-5 . (Model 42, s. 65, Ostatnia gwiazda dwudziestościanu )
•   Cromwell, Peter R. (1997). Wielościany . Wydawnictwo Uniwersytetu Cambridge. ISBN 0-521-66405-5 .
•   Jenkins, Gerald i Magdalen Bear. Ostateczna gwiazda dwudziestościanu: zaawansowany model matematyczny do wycięcia i sklejenia . Norfolk, Anglia: Tarquin Publications, 1985. ISBN 978-0-906212-48-6 .

Linki zewnętrzne

• Z instrukcją budowy modelu kolczatki ( .doc ) autorstwa Ralpha Jonesa
• W kierunku stellowania dwudziestościanu i fasetowania dwunastościanu przez Guya Inchbalda
• Weisstein, Eric W. „Pięćdziesiąt dziewięć stelacji dwudziestościanu” . MathWorld .
  • Weisstein, Eric W. „Echidnahedron” . MathWorld .
• Stelacje dwudziestościanu
• 59 stelacji dwudziestościanu
• VRML : http://www.georgehart.com/virtual-polyhedra/vrml/echidnahedron.wrl
• Netlib : Baza danych wielościanów, model 141

Godne uwagi stellacje dwudziestościanu
Regularny	Jednolite dublety			Regularne związki			Zwykła gwiazda	Inni
(Wypukły) dwudziestościan	Mały dwudziestościan triambiczny	Przyśrodkowy dwudziestościan triambiczny	Wielki dwudziestościan triambiczny	Związek pięciu ośmiościanów	Związek pięciu czworościanów	Związek dziesięciu czworościanów	Wielki dwudziestościan	Wykopany dwunastościan	Ostateczna stelacja
Proces stellacji na dwudziestościanie tworzy szereg powiązanych wielościanów i związków o symetrii dwudziestościanu .