Wielki dwudziestościan

Wielki dwudziestościan
Typ	Jednolity wielościan gwiazdy
Elementy	F = 32, E = 60 V = 30 (χ = 2)
Twarze po bokach	20{3}+12{5/2}
Diagram Coxetera
Symbol Wythoffa	2 | 3 5/2 2 | 3 5/3 2 | 3/2 5/2 2 | 3/2 5/3
Grupa symetrii	I h , [5,3], *532
Odnośniki do indeksu	U 54 , C 70 , W 94
Podwójny wielościan	Wielki rombowy triakontaedr
figura wierzchołka	3,5/2,3,5/2
skrót Bowersa	Kołowacizna

Model 3D wielkiego dwudziestościanu

W geometrii wielki dwudziestościan jest niewypukłym jednorodnym wielościanem o indeksie U ₅₄ . Ma 32 ściany (20 trójkątów i 12 pentagramów ), 60 krawędzi i 30 wierzchołków. Nadano mu symbol Schläfli r {3, 5 / 2 }. Jest to rektyfikacja dwunastościanu wielkiego gwiaździstego i dwudziestościanu wielkiego . Został odkryty niezależnie przez Hessa ( 1878 ), Badoureau ( 1881 ) i Pitscha ( 1882 ).

Powiązane wielościany

Figura jest rektyfikacją wielkiego dwudziestościanu lub wielkiego dwunastościanu gwiaździstego , podobnie jak (mały) dwudziestościan jest powiązany z (małym) dwudziestościanem i (małym) dwunastościanem , a sześcienny ośmiościan z sześcianem i ośmiościanem .

Dzieli swój układ wierzchołków z dwudziestościanem, który jest jego wypukłym kadłubem . W przeciwieństwie do dwudziestościanu wielkiego i dwudziestościanu wielkiego , dwudziestościan wielki nie jest stelacją dwudziestościanu, ale jego fasetą .

Dzieli również swój układ krawędzi z wielkim dwunastościanem (mając wspólne ściany trójkąta) oraz z dwunastościanem wielkim (mając wspólne ściany pentagramu).

Wielki dwudziestościan	Wielki dwunastościan hemidodecahedron	Wielki icosihemidodecahedron
Dwudziestościan ( wypukły kadłub )

Animowana sekwencja obcinania od { 5 / 2 , 3} do {3, 5 / 2 }

Ścięty wielki dwunastościan gwiaździsty jest zdegenerowanym wielościanem, z 20 trójkątnymi ścianami ze ściętych wierzchołków i 12 (ukrytymi) pięciokątnymi ścianami jako obcięciami oryginalnych ścian pentagramu, przy czym ten ostatni tworzy wielki dwunastościan wpisany wewnątrz i dzielący krawędzie dwudziestościanu.

Nazwa	Wielki gwiaździsty dwunastościan	Obcięty wielki dwunastościan gwiaździsty	Wielki dwudziestościan	Ścięty wielki dwudziestościan	Wielki dwudziestościan
Diagram Coxetera
Zdjęcie

Wielki rombowy triakontaedr

Wielki rombowy triakontaedr
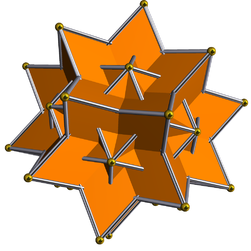
Typ	Gwiazda wielościanu
Twarz
Elementy	F = 30, E = 60 V = 32 (χ = 2)
Grupa symetrii	I h , [5,3], *532
Odnośniki do indeksu	DU 54
podwójny wielościan	Wielki dwudziestościan

Model 3D wielkiego trójścianu rombowego

Liczba podwójna wielkiego dwudziestościanu to wielki rombowy triacontahedron ; jest niewypukły, izościenny i izotoksalny . Ma 30 przecinających się rombowych ścian. Można go również nazwać wielkim gwiaździstym triakontaedrem.

Wielki triakontaścian rombowy można skonstruować, zwiększając rozmiar ścian rombowego triakontaścianu o współczynnik τ ³ = 1 + 2 τ = 2 + √ 5, gdzie τ jest złotym podziałem .

Zobacz też

• Lista jednolitych wielościanów
• Sześciokąt rombowy

Notatki

• Badoureau (1881), „Mémoire sur les les isoscèles”, Journal de l'École Polytechnique , 49 : 47–172
•   Hess, Edmund (1878), Vier archimedeische Polyeder höherer Art , Cassel. Cz. Kay, JFM 10.0346.03
•   Pitsch (1882), "Über halbreguläre Sternpolyeder", Zeitschrift für das Realschulwesen , 7 , JFM 14.0448.01
•    Wenninger , Magnus ( 1983 ) , modele podwójne , Cambridge University Press _ _

Linki zewnętrzne

• Weisstein, Eric W. „Wielki dwudziestościan” . MathWorld .
• Weisstein, Eric W. „Wielki trójścian rombowy” . MathWorld .
• Jednolite wielościany i liczby podwójne