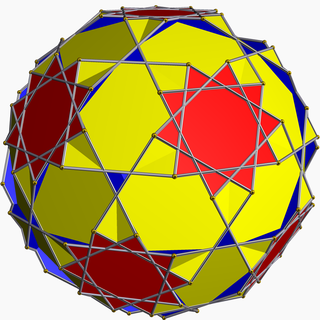
Obcięty dwunastościan

Obcięty dwunastościan
Typ	Jednolity wielościan gwiazdy
Elementy	F = 54, E = 180 V = 120 (χ = −6)
Twarze po bokach	30{4}+12{10}+12{10/3}
Diagram Coxetera
Symbol Wythoffa	2 5 5/3 |
Grupa symetrii	I h , [5,3], *532
Odnośniki do indeksu	U 59 , C 75 , W 98
Podwójny wielościan	Przyśrodkowy triacontahedron disdyakis
figura wierzchołka	4.10/9.10/3
skrót Bowersa	Rzuciłem

Model 3D ściętego dwunastościanu

W geometrii dwunastościan ścięty ( lub dwunastościan ścięty gwiaździście ) jest niewypukłym jednolitym wielościanem o indeksie U ₅₉ . Nadano mu symbol Schläfliego t _0,1,2 { 5 / 3 ,5}. Ma 54 ściany (30 kwadratów , 12 dziesięciokątów i 12 dekagramów ), 180 krawędzi i 120 wierzchołków. Centralny obszar wielościanu jest połączony z otoczeniem za pomocą 20 małych trójkątnych otworów.

Nazwa dwunastościanu ściętego jest nieco myląca: obcięcie dwunastościanu dałoby prostokątne ściany, a nie kwadraty, a ściany pentagramów dwunastościanu zamieniłyby się w ścięte pentagramy, a nie dekagramy. Jest to jednak quasitruncation dwunastościanu, jak zdefiniowali Coxeter, Longuet-Higgins & Miller (1954) . Z tego powodu jest również znany jako dwunastościan quasi ścięty . Coxeter i in. przypisać swoje odkrycie pracy opublikowanej w 1881 roku przez austriackiego matematyka Johanna Pitscha.

współrzędne kartezjańskie

Współrzędne kartezjańskie wierzchołków dwunastościanu ściętego to wszystkie trójki liczb uzyskane przez przesunięcia kołowe i zmiany znaków z następujących punktów (gdzie ${\ Displaystyle \ tau = {\ Frac {1 + {\ sqrt { 5}}}{2}}}$ to złoty podział ):

${\ Displaystyle (1,1,3); \ quad ({\ Frac {1} {\ tau}} {\ Frac {1} {\ tau ^ {2}}}, 2 \ tau); \ quad ( \tau ,{\frac {2}{\tau}},\tau ^{2});\quad (\tau ^{2},{\frac {1}{\tau ^{2}}},2 );\quad ({\sqrt {5}},1,{\sqrt {5}}).}$

Każdy z tych pięciu punktów ma osiem możliwych wzorów znaków i trzy możliwe przesunięcia kołowe, co daje w sumie 120 różnych punktów.

Jako graf Cayleya

Obcięty dwunastościan tworzy wykres Cayleya dla grupy symetrycznej na pięciu elementach, wygenerowany przez dwóch członków grupy: jednego, który zamienia pierwsze dwa elementy z pięciu krotek, i drugiego, który wykonuje operację przesunięcia kołowego na ostatnich czterech elementach. Oznacza to, że 120 wierzchołków wielościanu można umieścić w korespondencji jeden do jednego z 5! permutacje na pięciu elementach w taki sposób, że trzej sąsiedzi każdego wierzchołka to trzy permutacje utworzone z niego przez zamianę pierwszych dwóch elementów lub kołowe przesunięcie (w dowolnym kierunku) ostatnich czterech elementów.

Powiązane wielościany

Przyśrodkowy triacontahedron disdyakis

Przyśrodkowy triacontahedron disdyakis
Typ	Gwiazda wielościanu
Twarz
Elementy	F = 120, E = 180 V = 54 (χ = −6)
Grupa symetrii	I h , [5,3], *532
Odnośniki do indeksu	DU 59
podwójny wielościan	Obcięty dwunastościan

Model 3D przyśrodkowego triacontahedronu disdyakis

Przyśrodkowy triacontahedron disdyakis to niewypukły wielościan izoedryczny . Jest to podwójny z jednolitego ściętego dwunastościanu.

Zobacz też

• Lista

• jednolitych wielościanów Wenninger , Magnus ( 1983 ) , Dual Models , Cambridge University Press   

Linki zewnętrzne

• Weisstein, Eric W. „Ścięty dwunastościan” . MathWorld .
• Weisstein, Eric W. „Trójścian środkowy disdyakis” . MathWorld .