Zmiana okrężna
W matematyce kombinatorycznej przesunięcie kołowe jest operacją polegającą na przestawieniu wpisów w krotce poprzez przesunięcie ostatniego wpisu na pierwszą pozycję, przy jednoczesnym przesunięciu wszystkich pozostałych wpisów na następną pozycję lub wykonanie operacji odwrotnej. Przesunięcie kołowe jest szczególnym rodzajem permutacji cyklicznej , która z kolei jest szczególnym rodzajem permutacji . Formalnie przesunięcie kołowe jest permutacją σ n wpisów w krotce taką, że albo
- modulo n dla wszystkich wpisów ja = 1, ..., n
Lub
- modulo n , dla wszystkich wpisów ja = 1, ..., n .
Wynik wielokrotnego stosowania przesunięć kołowych do danej krotki jest również nazywany przesunięciami kołowymi krotki.
Na przykład wielokrotne stosowanie przesunięć kołowych do krotki czterokrotnej ( a , b , c , d ) daje kolejno
- ( re , za , b , do ),
- ( do , re , za , b ),
- ( b , do , re , za ),
- ( a , b , c , d ) (oryginalna czterokrotka),
a następnie sekwencja się powtarza; ta czterokrotna krotka ma zatem cztery różne przesunięcia kołowe. Jednak nie wszystkie n -krotki mają n różnych przesunięć kołowych. Na przykład krotka 4 ( a , b , a , b ) ma tylko 2 różne przesunięcia kołowe. Ogólnie liczba przesunięć kołowych n -krotki może być dowolnym dzielnikiem n , w zależności od wpisów krotki.
W programowaniu komputerowym obrót bitowy , znany również jako przesunięcie kołowe, jest operacją bitową, która przesuwa wszystkie bity swojego operandu. W przeciwieństwie do przesunięcia arytmetycznego , przesunięcie kołowe nie zachowuje bitu znaku liczby ani nie odróżnia wykładnika liczby zmiennoprzecinkowej od jej mantysy . W przeciwieństwie do przesunięcia logicznego wolne pozycje bitów nie są wypełniane zerami, ale bitami przesuniętymi poza sekwencję.
Wdrażanie zmian okrężnych
Przesunięcia kołowe są często używane w kryptografii w celu permutacji sekwencji bitów. Niestety wiele języków programowania, w tym C , nie ma operatorów ani standardowych funkcji dla przesunięć kołowych, mimo że praktycznie wszystkie procesory mają do tego bitowe instrukcje operacji (np. Intel x86 ma ROL i ROR). Jednak niektóre kompilatory mogą zapewniać dostęp do instrukcji procesora za pomocą funkcji wewnętrznych . Ponadto niektóre konstrukcje w standardowym ANSI C mogą być optymalizowane przez kompilator do instrukcji języka asemblera „obracaj” na procesorach, które mają taką instrukcję. Większość kompilatorów C rozpoznaje następujący idiom i kompiluje go do pojedynczej 32-bitowej instrukcji obracania.
/* * Operacje przesunięcia w C są zdefiniowane tylko dla wartości przesunięcia, które * nie są ujemne i są mniejsze niż sizeof(value) * CHAR_BIT. * Maska, używana z bitowym-and (&), zapobiega niezdefiniowanemu zachowaniu *, gdy liczba przesunięć wynosi 0 lub >= szerokość unsigned int. */ #include <stdint.h> // dla uint32_t, aby uzyskać obrót o szerokości 32 bitów, niezależnie od rozmiaru int. #include <limits.h> // for CHAR_BIT uint32_t rotl32 ( wartość uint32_t , liczba unsigned int ) { const unsigned int mask = CHAR_BIT * sizeof ( wartość ) - 1 ; liczba &= maska ; zwróć ( wartość << liczba ) | ( wartość >> ( - liczba i maska )); } uint32_t rotr32 ( wartość uint32_t , liczba int bez znaku ) { const unsigned int mask = CHAR_BIT * sizeof ( wartość ) -1 ; liczba &= maska ; return ( wartość >> liczba ) | ( wartość << ( - liczba i maska )); }
Ta bezpieczna i przyjazna dla kompilatorów implementacja została opracowana przez Johna Regehra i dopracowana przez Petera Cordesa.
Prostsza wersja jest często spotykana, gdy liczba jest ograniczona do zakresu od 1 do 31 bitów:
uint32_t rotl32 ( wartość uint32_t , liczba int bez znaku ) { zwracana wartość << liczba | wartość >> ( 32 - liczba ); }
Ta wersja jest niebezpieczna, ponieważ jeśli liczba wynosi 0 lub 32, prosi o przesunięcie 32-bitowe, co jest niezdefiniowanym zachowaniem w standardzie języka C. Jednak i tak ma tendencję do działania, ponieważ większość mikroprocesorów implementuje wartość >> 32 jako przesunięcie 32-bitowe (wytwarzające 0) lub przesunięcie 0-bitowe (wytwarzające pierwotną wartość ), a każda z nich daje poprawny wynik w tej aplikacji .
Przykład
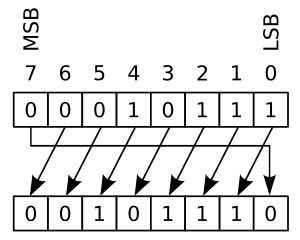
Gdyby sekwencja bitów 0001 0111 została poddana kołowemu przesunięciu o jedną pozycję bitową... (patrz ilustracje poniżej)
|
|
Gdyby sekwencja bitów 1001 0110 została poddana następującym operacjom:
| przesunięcie kołowe w lewo o 1 pozycję: | 0010 1101 |
| przesunięcie kołowe w lewo o 2 pozycje: | 0101 1010 |
| przesunięcie kołowe w lewo o 3 pozycje: | 1011 0100 |
| przesunięcie kołowe w lewo o 4 pozycje: | 0110 1001 |
| przesunięcie kołowe w lewo o 5 pozycji: | 1101 0010 |
| przesunięcie kołowe w lewo o 6 pozycji: | 1010 0101 |
| przesunięcie kołowe w lewo o 7 pozycji: | 0100 1011 |
| przesunięcie kołowe w lewo o 8 pozycji: | 1001 0110 |
| przesunięcie kołowe w prawo o 1 pozycję: | 0100 1011 |
| przesunięcie kołowe w prawo o 2 pozycje: | 1010 0101 |
| przesunięcie okrężne w prawo o 3 pozycje: | 1101 0010 |
| przesunięcie kołowe w prawo o 4 pozycje: | 0110 1001 |
| przesunięcie kołowe w prawo o 5 pozycji: | 1011 0100 |
| przesunięcie kołowe w prawo o 6 pozycji: | 0101 1010 |
| przesunięcie kołowe w prawo o 7 pozycji: | 0010 1101 |
| przesunięcie kołowe w prawo o 8 pozycji: | 1001 0110 |
Aplikacje
Kody cykliczne to rodzaj kodu blokowego , którego właściwość polega na tym, że przesunięcie kołowe słowa kodowego zawsze daje inne słowo kodowe. Motywuje to następującą ogólną definicję: Dla łańcucha s nad alfabetem Σ niech przesunięcie ( s ) oznacza zbiór przesunięć kołowych s , a dla zbioru L ciągów niech przesunięcie ( L ) oznacza zbiór wszystkich przesunięć kołowych struny w l . Jeśli L jest kodem cyklicznym, to shift ( L ) ⊆ L ; jest to warunek konieczny, aby L był językiem cyklicznym . Przesunięcie operacji ( L ) było badane w teorii języka formalnego . Na przykład, jeśli L jest językiem bezkontekstowym , to shift ( L ) jest znowu bezkontekstowy. Ponadto, jeśli L jest opisane przez wyrażenie regularne o długości n , istnieje wyrażenie regularne o długości O ( n3 ) opisujące przesunięcie ( L ).
Zobacz też
- Przekładnia bębnowa
- obiegowy
- Słowo Lyndona
- Naszyjnik — przedmiot podobny do krotki , ale dla którego przesunięcia kołowe są uważane za równoważne.