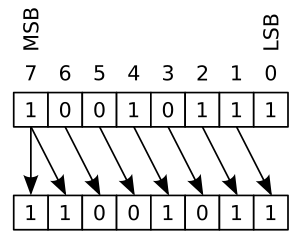
Przesunięcie arytmetyczne

Prawe przesunięcie arytmetyczne liczby binarnej o 1. Pusta pozycja w najbardziej znaczącym bicie jest wypełniona kopią oryginalnego MSB.

Arytmetyczne przesunięcie liczby binarnej w lewo o 1. Puste miejsce w najmniej znaczącym bicie jest wypełniane zerem.

Arytmetyczne operatory przesunięć w różnych językach programowania i procesorach
Język lub procesor	Lewy	Prawidłowy
ActionScript 3, Java , JavaScript , Python , PHP , Ruby , C , C++ , D , C# , Go , Julia , Rust (tylko typy ze znakiem), Swift (tylko typy ze znakiem)	`<`	`>>`
Ada	`Shift_w lewo`	`Shift_Right_Arithmetic`
Kotlin	`shl`	`sr`
standardowy ML	`<`	`~>>`
Verilog	`<<`	`>>>`
Język makr OpenVMS	@
Schemat	`przesunięcie arytmetyczne`
pospolity LISP	`popiół`
OCaml	`lsl`	`asr`
Haskella	`Przesunięcie.bitów danych`
Zgromadzenie, 68 tys	`ASL`	`ASR`
Montaż, x86	`SAL`	`SAR`
VHDL	`sla`	`śra`
RISC-V	`sll` , `sll`	`sra` , `sra`
Z80	`SLA`	`SRA`

W programowaniu komputerowym przesunięcie arytmetyczne jest operatorem przesunięcia , czasami nazywanym przesunięciem ze znakiem (chociaż nie ogranicza się do operandów ze znakiem). Dwa podstawowe typy to arytmetyczne przesunięcie w lewo i arytmetyczne przesunięcie w prawo . W przypadku liczb binarnych jest to operacja bitowa , która przesuwa wszystkie bity swojego operandu; każdy bit w argumencie jest po prostu przesuwany o określoną liczbę pozycji bitowych, a wolne pozycje bitowe są wypełniane . bit znaku w reprezentacjach liczb całkowitych ze znakiem) jest replikowany w celu wypełnienia wszystkich wolnych pozycji (jest to rodzaj rozszerzenia znaku ).

Niektórzy autorzy preferują terminy lepkie przesunięcie w prawo i przesunięcie w prawo z wypełnieniem zerowym odpowiednio dla przesunięć arytmetycznych i logicznych.

Przesunięcia arytmetyczne mogą być przydatne jako wydajne sposoby wykonywania mnożenia lub dzielenia liczb całkowitych ze znakiem przez potęgi dwójki. Przesunięcie w lewo o n bitów liczby binarnej ze znakiem lub bez znaku powoduje pomnożenie jej przez 2 ⁿ . Przesunięcie w prawo o n bitów liczby binarnej z dopełnieniem do dwóch ze znakiem powoduje podzielenie jej przez 2 ⁿ , ale zawsze zaokrągla w dół (w kierunku ujemnej nieskończoności). Różni się to od sposobu, w jaki zaokrąglanie jest zwykle wykonywane w dzieleniu liczb całkowitych ze znakiem (które zaokrągla się w kierunku 0). Ta rozbieżność doprowadziła do błędów w wielu kompilatorach.

Na przykład w zestawie instrukcji x86 instrukcja SAR (arytmetyczne przesunięcie w prawo) dzieli liczbę ze znakiem przez potęgę dwójki, zaokrąglając w kierunku ujemnej nieskończoności. Jednak instrukcja IDIV (dzielenia ze znakiem) dzieli liczbę ze znakiem, zaokrąglając w kierunku zera. Tak więc instrukcji SAR nie można zastąpić IDIV mocą dwóch instrukcji ani odwrotnie.

Definicja formalna

Formalna definicja przesunięcia arytmetycznego, zaczerpnięta z normy federalnej 1037C, jest następująca:

Przesunięcie stosowane do reprezentacji liczby w systemie liczbowym o stałej podstawie i systemie reprezentacji stałoprzecinkowej , w którym przesuwane są tylko znaki reprezentujące część stałoprzecinkową liczby. Przesunięcie arytmetyczne jest zwykle równoważne pomnożeniu liczby przez dodatnią lub ujemną całkowitą potęgę podstawy, z wyjątkiem efektu zaokrąglenia; porównać przesunięcie logiczne z przesunięciem arytmetycznym, zwłaszcza w przypadku reprezentacji zmiennoprzecinkowej .

Ważnym słowem w definicji FS 1073C jest „zwykle”.

Równoważność arytmetycznych i logicznych przesunięć w lewo i mnożenia

Arytmetyczne przesunięcia w lewo są równoważne mnożeniu przez (dodatnią, całkowitą) potęgę podstawy (np. mnożenie przez potęgę 2 dla liczb binarnych). Logiczne przesunięcia w lewo są również równoważne, z wyjątkiem mnożenia i przesunięć arytmetycznych, które mogą powodować przepełnienie arytmetyczne , podczas gdy przesunięcia logiczne nie.

Nierównoważność arytmetycznego przesunięcia w prawo i dzielenia

Jednak arytmetyczne przesunięcia w prawo są głównymi pułapkami dla nieostrożnych, szczególnie w przypadku zaokrąglania ujemnych liczb całkowitych. Na przykład w zwykłej z uzupełnieniem do dwóch , −1 jest reprezentowane jako same jedynki. Dla 8-bitowej liczby całkowitej ze znakiem jest to 1111 1111. Arytmetyczne przesunięcie w prawo o 1 (lub 2, 3, ..., 7) daje ponownie 1111 1111, co nadal wynosi -1. Odpowiada to zaokrągleniu w dół (w kierunku ujemnej nieskończoności), ale nie jest to zwykła konwencja dzielenia.

Często stwierdza się, że arytmetyczne przesunięcia w prawo są równoważne dzieleniu przez (dodatnią, całkowitą) potęgę podstawy (np. dzielenie przez potęgę 2 dla liczb binarnych), a zatem dzielenie przez potęgę podstawy może być zoptymalizowany przez zaimplementowanie go jako arytmetycznego przesunięcia w prawo. (Przesuwak jest znacznie prostszy niż dzielnik . W przypadku większości procesorów instrukcje przesunięcia będą wykonywane szybciej niż instrukcje dzielenia) . Duża liczba podręczników programowania, podręczników i innych specyfikacji z lat 60. i 70 . i ANSI składają takie niepoprawne oświadczenia ^{[ potrzebna strona ]} .

Logiczne przesunięcia w prawo są równoważne dzieleniu przez potęgę podstawy (zwykle 2) tylko dla liczb dodatnich lub bez znaku. Arytmetyczne przesunięcia w prawo są równoważne logicznym przesunięciom w prawo dla liczb dodatnich ze znakiem. Arytmetyczne przesunięcia w prawo dla liczb ujemnych w dopełnieniu N-1 (zwykle dopełnieniem do dwóch ) jest z grubsza równoważne dzieleniu przez potęgę podstawy (zwykle 2), gdzie dla liczb nieparzystych stosuje się zaokrąglanie w dół (nie w kierunku 0, jak zwykle oczekiwano).

Arytmetyczne przesunięcia w prawo dla liczb ujemnych są równoważne z dzieleniem przy użyciu zaokrąglenia w kierunku 0 w reprezentacji liczb ze znakiem w uzupełnieniu do jednej , jak to było używane w niektórych historycznych komputerach, ale nie jest to już w powszechnym użyciu.

Obsługa problemu w językach programowania

Norma ISO (1999) dla języka programowania C definiuje prawy operator przesunięcia w kategoriach dzielenia przez potęgi 2. Z powodu powyższej nierównoważności norma wyraźnie wyklucza z tej definicji przesunięcia w prawo liczb ze znakiem, które mają wartości ujemne. Nie określa zachowania operatora przesunięcia w prawo w takich okolicznościach, ale zamiast tego wymaga, aby każdy indywidualny kompilator C zdefiniował zachowanie przesuwania wartości ujemnych w prawo.

Aplikacje

W aplikacjach, w których pożądane jest spójne zaokrąglanie w dół, przydatne są arytmetyczne przesunięcia w prawo dla wartości ze znakiem. Przykładem jest zmniejszanie współrzędnych rastrowych o potęgę dwójki, co pozwala na zachowanie równych odstępów. Na przykład przesunięcie w prawo o 1 wysyła 0, 1, 2, 3, 4, 5, ... do 0, 0, 1, 1, 2, 2, ... i -1, -2, -3, −4, ... do −1, −1, −2, −2, ..., zachowując równe odstępy jako −2, −2, −1, −1, 0, 0, 1, 1, 2, 2 , ... W przeciwieństwie do tego, dzielenie liczb całkowitych z zaokrągleniem do zera wysyła −1, 0 i 1 wszystkie do 0 (3 punkty zamiast 2), dając −2, −1, −1, 0, 0, 0, 1, 1, 2, 2, ... zamiast tego, co jest nieregularne przy 0.

Notatki

^ Operator >> w C i C++ niekoniecznie jest przesunięciem arytmetycznym. Zwykle jest to tylko przesunięcie arytmetyczne, jeśli jest używane z liczbą całkowitą ze znakiem po lewej stronie. Jeśli zamiast tego zostanie użyty na typie całkowitym bez znaku, będzie to logiczne .
^ Operator arytmetycznego przesunięcia w prawo Verilog faktycznie wykonuje przesunięcie arytmetyczne tylko wtedy, gdy pierwszy operand jest podpisany. Jeśli pierwszy operand jest bez znaku, operator faktycznie wykonuje logiczne przesunięcie w prawo.
^ W języku makr OpenVMS to, czy przesunięcie arytmetyczne jest w lewo, czy w prawo, zależy od tego, czy drugi operand jest dodatni, czy ujemny. To jest niezwykłe. W większości języków programowania dwa kierunki mają różne operatory, przy czym operator określa kierunek, a drugi operand jest domyślnie dodatni. (Niektóre języki, takie jak Verilog, wymagają konwersji wartości ujemnych na wartości dodatnie bez znaku. Niektóre języki, takie jak C i C++, nie mają zdefiniowanego zachowania, jeśli używane są wartości ujemne.) [ ^{potrzebna strona ]}
^ W schemacie przesunięcie arytmetyczne może być przesunięciem zarówno w lewo, jak iw prawo, w zależności od drugiego operandu, bardzo podobnie do języka makr OpenVMS, chociaż schemat R6RS dodaje zarówno warianty -right, jak i -left .
^ Klasa Bits z modułu Data.Bits firmy Haskell definiuje zarówno shift przyjmujący argument ze znakiem, jak i shiftL / shiftR przyjmujący argumenty bez znaku. To są izomorficzne ; dla nowych definicji programista musi podać tylko jeden z dwóch formularzy, a drugi formularz zostanie automatycznie zdefiniowany na podstawie podanego.
^ Operator arytmetyczny przesunięcia w lewo VHDL jest niezwykły. Zamiast wypełniać LSB wyniku zerem, kopiuje oryginalny LSB do nowego LSB. Chociaż jest to dokładne lustrzane odbicie arytmetycznego przesunięcia w prawo, nie jest to konwencjonalna definicja operatora i nie jest równoważne mnożeniu przez potęgę 2. W standardzie VHDL 2008 to dziwne zachowanie pozostawiono niezmienione (ze względu na kompatybilność wsteczną ) dla typów argumentów, które nie mają wymuszonej interpretacji numerycznej (np. BIT_VECTOR), ale 'SLA' dla bez znaku i ze znakiem zachowuje się w oczekiwany sposób (tzn. skrajne prawe pozycje są wypełnione zerami). Funkcja przesunięcia w lewo logiczna VHDL (SLL) implementuje wspomniane „standardowe” przesunięcie arytmetyczne.
^ Standard C miał nie ograniczać języka C do architektur dopełnienia do jedności lub dopełnienia do dwóch. W przypadkach, w których zachowania reprezentacji dopełnienia do jedynek i dopełnienia do dwóch różnią się, jak na przykład ten, standard wymaga, aby poszczególne kompilatory C dokumentowały zachowanie ich docelowych architektur. dokumentacja dla GNU Compiler Collection (GCC) dokumentuje jego zachowanie jako wykorzystujące rozszerzenie znaku.

Odsyłacz

Wykorzystane źródła

Ten artykuł zawiera materiały należące do domeny publicznej z normy federalnej 1037C . Administracja usług ogólnych . Zarchiwizowane od oryginału w dniu 2022-01-22.

Knuth, Donald (1969). Sztuka programowania komputerowego , tom 2 — Algorytmy półnumeryczne . Czytanie, Massachusetts: Addison-Wesley. s. 169–170.
Steele, Guy L. (listopad 1977). „Przesunięcie arytmetyczne uważane za szkodliwe” . Archiwum powiadomień ACM SIGPLAN . Nowy Jork: ACM Press. 12 (11): 61–69. doi : 10.1145/956641.956647 . hdl : 1721.1/6090 . S2CID 15420308 . Zarchiwizowane od oryginału w dniu 22 września 2017 r.
„3.7.1 Operator przesunięcia arytmetycznego” . Podręcznik referencyjny MAKRO VAX i zestawu instrukcji . Dokumentacja systemów HP OpenVMS . Firma deweloperska Hewlett-Packard. Kwiecień 2001. Zarchiwizowane od oryginału w dniu 08.08.2011.
„Języki programowania — C”. ISO/IEC 9899:1999. Międzynarodowa Organizacja Normalizacyjna . 1999. {{ cytuj dziennik }} : Cytuj dziennik wymaga |journal= ( pomoc )
Hyde, Randall (1996-09-26). „ROZDZIAŁ SZÓSTY: ZESTAW INSTRUKCJI 80x86 (część 3)” . Sztuka programowania w języku asemblera . Zarchiwizowane od oryginału w dniu 2007-11-23 . Źródło 2007-11-28 .
„Implementacja C” . podręcznik GCC . Fundacja Wolnego Oprogramowania . 2008.

[3] Operator >> w C i C++ niekoniecznie jest przesunięciem arytmetycznym. Zwykle jest to tylko przesunięcie arytmetyczne, jeśli jest używane z liczbą całkowitą ze znakiem po lewej stronie. Jeśli zamiast tego zostanie użyty na typie całkowitym bez znaku, będzie to logiczne .

[5] Operator arytmetycznego przesunięcia w prawo Verilog faktycznie wykonuje przesunięcie arytmetyczne tylko wtedy, gdy pierwszy operand jest podpisany. Jeśli pierwszy operand jest bez znaku, operator faktycznie wykonuje logiczne przesunięcie w prawo.

[7] W języku makr OpenVMS to, czy przesunięcie arytmetyczne jest w lewo, czy w prawo, zależy od tego, czy drugi operand jest dodatni, czy ujemny. To jest niezwykłe. W większości języków programowania dwa kierunki mają różne operatory, przy czym operator określa kierunek, a drugi operand jest domyślnie dodatni. (Niektóre języki, takie jak Verilog, wymagają konwersji wartości ujemnych na wartości dodatnie bez znaku. Niektóre języki, takie jak C i C++, nie mają zdefiniowanego zachowania, jeśli używane są wartości ujemne.) [ ^{potrzebna strona ]}

[scheme-8] W schemacie przesunięcie arytmetyczne może być przesunięciem zarówno w lewo, jak iw prawo, w zależności od drugiego operandu, bardzo podobnie do języka makr OpenVMS, chociaż schemat R6RS dodaje zarówno warianty -right, jak i -left .

[9] Klasa Bits z modułu Data.Bits firmy Haskell definiuje zarówno shift przyjmujący argument ze znakiem, jak i shiftL / shiftR przyjmujący argumenty bez znaku. To są izomorficzne ; dla nowych definicji programista musi podać tylko jeden z dwóch formularzy, a drugi formularz zostanie automatycznie zdefiniowany na podstawie podanego.

[10] Operator arytmetyczny przesunięcia w lewo VHDL jest niezwykły. Zamiast wypełniać LSB wyniku zerem, kopiuje oryginalny LSB do nowego LSB. Chociaż jest to dokładne lustrzane odbicie arytmetycznego przesunięcia w prawo, nie jest to konwencjonalna definicja operatora i nie jest równoważne mnożeniu przez potęgę 2. W standardzie VHDL 2008 to dziwne zachowanie pozostawiono niezmienione (ze względu na kompatybilność wsteczną ) dla typów argumentów, które nie mają wymuszonej interpretacji numerycznej (np. BIT_VECTOR), ale 'SLA' dla bez znaku i ze znakiem zachowuje się w oczekiwany sposób (tzn. skrajne prawe pozycje są wypełnione zerami). Funkcja przesunięcia w lewo logiczna VHDL (SLL) implementuje wspomniane „standardowe” przesunięcie arytmetyczne.

[19] Standard C miał nie ograniczać języka C do architektur dopełnienia do jedności lub dopełnienia do dwóch. W przypadkach, w których zachowania reprezentacji dopełnienia do jedynek i dopełnienia do dwóch różnią się, jak na przykład ten, standard wymaga, aby poszczególne kompilatory C dokumentowały zachowanie ich docelowych architektur. dokumentacja dla GNU Compiler Collection (GCC) dokumentuje jego zachowanie jako wykorzystujące rozszerzenie znaku.