Wielki zadarty dwudziestościan

Wielki zadarty dwudziestościan
Typ	Jednolity wielościan gwiazdy
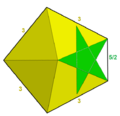
Elementy	F = 92, E = 150 V = 60 (χ = 2)
Twarze po bokach	(20+60){3}+12{5/2}
Diagram Coxetera
Symbol Wythoffa	| 2 5/2 3
Grupa symetrii	I, [5,3] + , 532
Odnośniki do indeksu	U 57 , C 88 , W 113
Podwójny wielościan	Wielki pięciokątny sześciokąt
figura wierzchołka	3 4 .5/2
skrót Bowersa	Gosid

Model 3D wielkiego zadartego dwudziestościanu

W geometrii wielki zadarty dwudziestościan jest niewypukłym jednorodnym wielościanem o indeksie U ₅₇ . Ma 92 ściany (80 trójkątów i 12 pentagramów ), 150 krawędzi i 60 wierzchołków. Można to przedstawić za pomocą symbolu Schläfliego sr{ 5 / 2 ,3} i diagramu Coxetera-Dynkina .

Ten wielościan jest zadartym członkiem rodziny, która obejmuje wielki dwudziestościan , wielki dwunastościan gwiaździsty i wielki dwudziestościan wielki .

W książce Polyhedron Models autorstwa Magnusa Wenningera wielościan jest błędnie nazywany wielkim odwróconym dwudziestościanem i na odwrót.

współrzędne kartezjańskie

Współrzędne kartezjańskie wierzchołków dwudziestościanu wielkiego zadartego są wszystkimi parzystymi permutacjami

(±2α, ±2, ±2β),

(±(α−βτ−1/τ), ±(α/τ+β−τ), ±(−ατ−β/τ−1)), (±

( ατ−β/τ+1), ±(−α−βτ+1/τ), ±(−α/τ+β+τ)), (±(ατ−β/τ−1), ±(α

+ βτ+1/τ), ±(−α/τ+β−τ)) i

(±(α−βτ+1/τ), ±(−α/τ−β−τ), ±(−ατ−β /τ+1)),

z parzystą liczbą znaków plus, gdzie

α = ξ-1/ξ

I

β = −ξ/τ+1/τ ² −1/(ξτ),

gdzie τ = (1+ √ 5 )/2 to złoty środek , a ξ to ujemny pierwiastek rzeczywisty z ξ ³ −2ξ=−1/τ, czyli w przybliżeniu −1,5488772. Biorąc nieparzyste permutacje powyższych współrzędnych z nieparzystą liczbą znaków plus, otrzymujemy inną postać, enancjomorf drugiej .

Promień okręgu dla jednostkowej długości krawędzi wynosi

${\ Displaystyle R = {\ Frac {1} {2}} {\ sqrt {\ Frac {2-x} {1-x}}} = 0,64502 \ kropki }$

gdzie ${\ Displaystyle x}$ jest odpowiednim pierwiastkiem ${\ Displaystyle x ^ {3} + 2x ^ {2} = {\ duży (}{\ tfrac { 1\pm {\sqrt {5}}}{2}}{\Duży)}^{2}}$ . Cztery pozytywne rzeczywiste korzenie sekstyku w R $\ Displaystyle R ^ {2},}$

${\ Displaystyle 4096R ^ {12} -27648R ^ {10} + 47104R ^ {8} -35776R ^ { 6}+13872R^{4}-2696R^{2}+209=0}$

to promienie okalające dwunastościan zadarty (U ₂₉ ), dwudziestościan wielki zadarty ( U ₅₇ ), dwudziestościan wielki odwrócony zadarty ( U ₆₉ ) i dwudziestościan wielki retrosnub (U ₇₄ ).

Powiązane wielościany

Wielki pięciokątny sześciokąt

Wielki pięciokątny sześciokąt
Typ	Gwiazda wielościanu
Twarz
Elementy	F = 60, E = 150 V = 92 (χ = 2)
Grupa symetrii	I, [5,3] + , 532
Odnośniki do indeksu	DU 57
podwójny wielościan	Wielki zadarty dwudziestościan

Model 3D wielkiego pięciokątnego sześciokąta

Wielki pięciokątny sześciokąt (lub wielki petaloid ditriacontahedron ) jest niewypukłym wielościanem izoedralnym i podwójnym w stosunku do jednolitego dwudziestościanu wielkiego zadartego . Ma 60 przecinających się nieregularnych pięciokątnych ścian, 120 krawędzi i 92 wierzchołki.

Proporcje

Oznacz złoty podział przez ${\ displaystyle \ phi}$ . Niech $\$ ujemnym zerem wielomianu $\$ . Wtedy każda pięciokątna ściana ma cztery równe kąty ${\ Displaystyle \ arccos (\ xi) \ około 101,508 \, 325 \, 512 \, 64 ^ {\ circ}}$ i jeden kąt ${\ Displaystyle \ arccos (- \ phi ^ {- 1} + \ phi ^ {- 2} \ xi) \ około 133,966 \ 697 \ 949 \ 42 ^ {\ circ}}$ . Każda ściana ma trzy długie i dwie krótkie krawędzie. stosunek ${\ displaystyle l}$ między długościami długiej i krótkiej krawędzi jest dana przez

${\ Displaystyle l = {\ Frac {2-4 \ xi ^ {2}} {1-2 \ xi}} \ około 1,315 \, 765 \ ,089\,00}$ .

Kąt dwuścienny równa się ${\ Displaystyle \ arccos (\ xi / (\ xi + 1)) \ około 104,432 \, 268 \, 611 \, 86 ^ {\cyrk}}$ . Część każdej ściany leży wewnątrz bryły, dlatego jest niewidoczna w modelach bryłowych. Pozostałe dwa zera wielomianu odgrywają podobną rolę w opisie wielkiego odwróconego pięciokąta sześciokątnego i ${\ displaystyle P}$ wielki pentagramowy heksekontahedr .

Zobacz też

• Lista jednolitych wielościanów
• Wielki odwrócony zadarty dwudziestościan
• Wielki retrosnub dwudziestościan

•    Wenninger, Magnus (1983), modele podwójne , Cambridge University Press , ISBN 978-0-521-54325-5 , MR 0730208

Linki zewnętrzne

• Weisstein, Eric W. „Wielki pięciokątny sześciokąt” . MathWorld .
• Weisstein, Eric W. „Wielki zadarty dwudziestościan” . MathWorld .