Rombidodekadodziesięciościan

Rombidodekadodziesięciościan
Typ	Jednolity wielościan gwiazdy
Elementy	F = 54, E = 120 V = 60 (χ = −6)
Twarze po bokach	30{4}+12{5}+12{5/2}
Diagram Coxetera
Symbol Wythoffa	5/2 5 | 2
Grupa symetrii	I h , [5,3], *532
Odnośniki do indeksu	U 38 , C 48 , W 76
Podwójny wielościan	Sześciokąt naramienny przyśrodkowy
figura wierzchołka	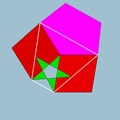4,5/2,4,5
skrót Bowersa	Raded

Model 3D rombidodekadodecaedru

W geometrii rombidodekadodecahedron jest niewypukłym jednolitym wielościanem , indeksowanym jako U ₃₈ . Ma 54 ściany (30 kwadratów , 12 pięciokątów i 12 pentagramów ), 120 krawędzi i 60 wierzchołków. Otrzymuje on symbol Schläfliego t _0,2 { 5 / 2 ,5} , a dzięki konstrukcji Wythoffa ten wielościan można również nazwać kantelowanym dwunastościanem wielkim .

współrzędne kartezjańskie

Współrzędne kartezjańskie wierzchołków jednorodnego wielkiego rombikozydodekahedru są parzystymi permutacjami

(±1/τ ² , 0, ±τ ² )

(±1, ±1, ± √ 5 )

(±2, ±1/τ, ±τ)

gdzie τ = (1+ √ 5 )/2 to złoty podział (czasami zapisywany jako φ).

Powiązane wielościany

Dzieli swój układ wierzchołków z jednolitymi związkami 10 lub 20 trójkątnych graniastosłupów . Dodatkowo dzieli swoje krawędzie z dwudziestościanem dwudziestościanu (mający wspólne ściany pięciokątne i pentagramowe) oraz rombicosaedrem (mający wspólne ściany kwadratowe).

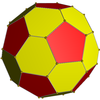wypukły kadłub	Rombidodekadodziesięciościan	Dwudziestościan dwunastościanu
romboidalny	Związek dziesięciu graniastosłupów trójkątnych	Związek dwudziestu trójkątnych graniastosłupów

Sześciokąt naramienny przyśrodkowy

Sześciokąt naramienny przyśrodkowy
Typ	Gwiazda wielościanu
Twarz
Elementy	F = 60, E = 120 V = 54 (χ = −6)
Grupa symetrii	I h , [5,3], *532
Odnośniki do indeksu	DU 38
podwójny wielościan	Rombidodekadodziesięciościan

Model 3D przyśrodkowego sześciokąta naramiennego

sześciokąt naramienny (lub środkowo-lancetowy ditriacontahedron ) jest niewypukłym wielościanem równoramiennym . Jest to liczba podwójna rombidodekadodekaedru. Ma 60 przecinających się czworobocznych ścian.

Zobacz też

• Lista

• jednolitych wielościanów Wenninger , Magnus ( 1983 ) , Dual Models , Cambridge University Press   

Linki zewnętrzne

• Weisstein, Eric W. „Rhombidodecadodecahedron” . MathWorld .
• Weisstein, Eric W. „Przyśrodkowy sześcian naramienny” . MathWorld .
• Jednolite wielościany i liczby podwójne