Hemiwielościan

W geometrii półścian jest jednolitym wielościanem gwiaździstym, którego niektóre ściany przechodzą przez jego środek. Te „hemi” ściany leżą równolegle do ścian innego symetrycznego wielościanu, a ich liczba jest równa połowie liczby ścian tego innego wielościanu - stąd przedrostek „hemi”.

Przedrostek „hemi” jest również używany w odniesieniu do pewnych rzutowych wielościanów , takich jak hemi-cube , które są obrazem mapy 2 do 1 kulistego wielościanu o centralnej symetrii .

Symbol Wythoffa i figura wierzchołka

  Ich symbole Wythoffa mają postać ^p / _{( p - q )} ^p / _q | r ; ich figury wierzchołków to skrzyżowane czworoboki . Są zatem spokrewnieni z kantelowanymi wielościanami, które mają podobne symbole Wythoffa. Konfiguracja wierzchołków to ^p / _q .2 r . ^p / _{( p - q )} .2 r . Ściany 2 r -gonów przechodzą przez środek modelu: jeśli są reprezentowane jako ściany kulistych wielościanów , pokrywają całą półkulę, a ich krawędzie i wierzchołki leżą wzdłuż koła wielkiego . Notacja ^p / _{( p - q )} implikuje ścianę { ^p / _q } obracającą się do tyłu wokół figury wierzchołka.

Dziewięć form wymienionych wraz z ich symbolami Wythoffa i konfiguracjami wierzchołków to:

Tetrahemisześcian 3 / 2 3 | 2 (3.4.3 / 2.4 ) ( p / q = 3, r = 2 )	ośmiościan 3 / 2 3 | 3 (3,6.3 / 2,6 ) ( p / q = 3, r = 3 )	Mały dwudziestosześcianu 3 / 2 3 | 5 (3.10.3 / 2.10 ) ( p / q = 3, r = 5)	Wielki dwudziestosześcian 3 / 2 3 | 5 / 3 (3. 10 / 3 . 3 / 2 . 10 / 3 ) ( p / q = 3, r = 5 / 3 )	Mały dwunastościan 5 / 3 5 / 2 | 3 ( 5 / 2 .6. 5 / 3 .6) ( p / q = 5 / 2 , r = 3)
	Sześcian hemiośmiościan 4 / 3 4 | 3 (4,6,4 / 3,6 ) ( p / q = 4, r = 3 )	Mały dwunastościan hemidodecahedron 5 / 4 5 | 5 (5.10. 5 / 4 .10) ( p / q = 5, r = 5)	Wielki dwunastościan hemidodecahedron 5 / 3 5 / 2 | 5 / 3 ( 5 / 2 . 10 / 3 . 5 / 3 . 10 / 3 ) ( p / q = 5 / 2 , r = 5 / 3 )	Sześcian dwunastościan wielki 5 / 4 5 | 3 (5,6,5 / 4,6 ) ( p / q = 5, r = 3)

Zauważ, że kalejdoskopowa konstrukcja Wythoffa generuje nieorientowalne wielościany (wszystkie oprócz ośmiościanu) jako podwójne pokrycie (dwa zbieżne hemiwielościany).

Na płaszczyźnie euklidesowej sekwencja hemipolyhedra jest kontynuowana z następującymi czterema nachyleniami gwiazd, gdzie apeirogony pojawiają się jako wspomniane wielokąty równikowe:

Oryginalna płytka rektyfikowana	Schemat krawędzi	Solidny	Konfiguracja wierzchołków	Wythoffa	Symetria
Płytki kwadratowe			4.∞.4/3.∞ 4.∞.-4.∞	4/3 4 | ∞	p4m
Płytki trójkątne			(3.∞.3.∞.3.∞)/2	3/2 | 3 ∞	p6m
Dachówka trójsześciokątna			6.∞.6/5.∞ 6.∞.-6.∞	6/5 6 | ∞
			∞.3.∞.3/2 ∞.3.∞.-3	3/2 3 | ∞

Z tych czterech nachyleń tylko 6/5 6 | ∞ jest generowane jako podwójne pokrycie przez konstrukcję Wythoffa.

Orientowalność

Tylko ośmiościan ośmiościan reprezentuje orientowalną powierzchnię; pozostałe hemipolihedry mają powierzchnie nieorientowane lub jednostronne. Dzieje się tak, ponieważ poruszając się po równiku 2 r -gon, ściany ^p / _q -gonal na przemian wskazują „w górę” i „w dół”, więc dowolne dwa kolejne mają przeciwne zwroty. Jest to równoznaczne z żądaniem, aby ^p / _q -gonom w odpowiednich quasiregularnych wielościanach poniżej można alternatywnie nadać orientację dodatnią i ujemną. Ale jest to możliwe tylko dla trójkątów ośmiościanu sześciennego (odpowiadających trójkątom ośmiościanu, jedynego regularnego wielościanu z parzystą liczbą ścian spotykających się w wierzchołku), które są dokładnie niehemi ścianami ośmiościanu.

Podwójne z hemipolyhedra

Ponieważ hemiwielościany mają ściany przechodzące przez środek, figury podwójne mają odpowiadające im wierzchołki w nieskończoności; poprawnie, na rzeczywistej płaszczyźnie rzutowej w nieskończoności. W Dual Models Magnusa Wenningera są one reprezentowane przez przecinające się graniastosłupy , z których każdy rozciąga się w obu kierunkach do tego samego wierzchołka w nieskończoności, aby zachować symetrię. W praktyce pryzmaty modelowe są obcinane w dogodnym dla twórcy miejscu. Wenninger zasugerował, że te postacie należą do nowej klasy figury gwiezdne , zwane stellacjami do nieskończoności . Jednak zasugerował również, że ściśle mówiąc nie są one wielościanami, ponieważ ich konstrukcja nie jest zgodna ze zwykłymi definicjami.

Istnieje 9 takich duali, dzielących tylko 5 różnych zewnętrznych form, z których cztery istnieją w pozornie identycznych parach. Członkowie danej wizualnie identycznej pary różnią się układem prawdziwych i fałszywych wierzchołków (fałszywy wierzchołek to miejsce, w którym dwie krawędzie przecinają się, ale nie łączą). Formy zewnętrzne to:

Tetrahemiheksakron	Oktahemioktakron i heksahemioktakron	Mały icosihemidodecacron i mały dodecahemidodecacron	Wielki dodecahemidodecacron i wielki icosihemidodecacron	Dodecahemicosacron wielki i mały dodecahemicosacron
3 przecinające się nieskończone kwadratowe graniastosłupy	4 przecinające się nieskończone sześciokątne graniastosłupy	6 przecinających się nieskończonych graniastosłupów dziesięciokątnych	6 przecinających się nieskończonych graniastosłupów dekagramowych	10 przecinających się nieskończonych sześciokątnych pryzmatów

Związek z wielościanami quasiregularnymi

Hemipolihedry występują w parach jako fasetki quasiregularnych wielościanów z czterema ścianami w wierzchołku. Te quasiregularne wielościany mają konfigurację wierzchołków m . rz . m . n i ich krawędzie, oprócz tworzenia ścian m- i n -gonalnych, tworzą również pół-ściany hemipolihedry. Zatem półściany można wyprowadzić z wielościanów quasiregularnych, odrzucając albo m -gony, albo n -gony (aby zachować dwie ściany na krawędzi), a następnie wstawienie półek. Ponieważ m -kąty lub n -kąty, z każdego quasiregularnego wielościanu można wyprowadzić jeden z dwóch półścianów, z wyjątkiem ośmiościanu jako czworościanu , gdzie m = n = 3, a dwa fasetki są przystające. (Ta konstrukcja nie działa w przypadku quasiregularnych wielościanów z sześcioma ścianami w wierzchołku, znanych również jako dwuścienne wielościany , ponieważ ich krawędzie nie tworzą żadnych regularnych półścian).

Ponieważ hemipolihedry, podobnie jak quasiregularne wielościany, również mają dwa rodzaje ścian naprzemiennie wokół każdego wierzchołka, czasami są one również uważane za quasiregularne.

Wielościan kwaziregularny m . rz . m . N	Hemi-twarze ( h -gons)	Hemipolihedron z odrzuconymi m -gonami n . godz . n / n - 1 . H	Hemipolihedron z odrzuconymi n -kątami m . godz . m / m - 1 . H
Czworościan 3.3.3.3 m = 3, n = 3	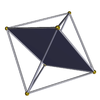kwadraty {4}	Tetrahemisześcian 3,4,3/2,4	Tetrahemisześcian 3,4,3/2,4
Sześcienny ośmiościan 3,4,3,4 m = 3, n = 4	sześciokąty {6}	Sześcian hemiośmiościan 4,6,4/3,6	ośmiościan 3,6,3/2,6
Dwudziestościan 3,5,3,5 m = 3, n = 5	dziesięciokąty {10}	Mały dwunastościan hemidodecahedron 5,10,5/4,10	Mały dwudziestościan dwudziestościanu 3.10.3/2.10
dwunastościan 5,5/2,5,5/2 m = 5, n = 5/2	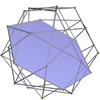sześciokąty {6}	Mały dwunastościan sześciokątny 5/2,6,5/3,6	Dwunastościan wielki dwunastościan 5,6,5/4,6
Dwudziestościan wielki 3,5/2,3,5/2 m = 3, n = 5/2	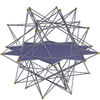dekagramy {10/3}	Sześcian dwunastościan wielki 5/2,10/3,5/3,10/3	Dwudziestosześcian wielki 3,10/3,3/2,10/3

Tutaj m i n odpowiadają ^p / _q powyżej, a h odpowiada 2 r powyżej.

•     Coxetera, Harolda Scotta MacDonalda ; Longuet-Higgins, MS; Miller, JCP (1954), „Jednolite wielościany”, Philosophical Transactions of the Royal Society of London. Seria A. Nauki matematyczne i fizyczne , The Royal Society, 246 (916): 401–450, doi : 10.1098/rsta.1954.0003 , ISSN 0080-4614 , JSTOR 91532 , MR 0062446
•    Wenninger, Magnus (1974), Polyhedron Models , Cambridge University Press , ISBN 978-0-521-09859-5 , MR 0467493 (modele Wenningera: 67, 68, 78, 89, 91, 100, 102, 106, 107)
•    Wenninger, Magnus (1983), modele podwójne , Cambridge University Press , ISBN 978-0-521-54325-5 , MR 0730208
• Har'El, Z. Jednolite rozwiązanie dla jednolitych wielościanów. , Geometriae Dedicata 47, 57-110, 1993. Zvi Har'El (Strona 10, 5.2. Hemi polyhedra p p'|r.)

Linki zewnętrzne

• Glosariusz wielościenny Stelli
• Versi-regularne wielościany w wizualnych wielościanach