Związek pięciu ośmiościanów
| Związek pięciu ośmiościanów | |
|---|---|
 (patrz tutaj, aby zobaczyć model 3D) |
|
| Typ | Regularny związek |
| Indeks | UC 17 , W 23 |
| Symbol Coxetera | [5{3,4}]2{3,5} |
|
Pierwiastki (jako związek) |
5 ośmiościanów : F = 40, E = 60, V = 30 |
| Podwójny związek | Związek pięciu kostek |
| Grupa symetrii | dwudziestościenny ( I h ) |
| Podgrupa ograniczająca się do jednego składnika | pirytoedryczny ( T h ) |

Związek . pięciu ośmiościanów jest jednym z pięciu regularnych związków wielościanów Ten wielościan może być postrzegany jako wielościenna gwiazda lub związek . Ten związek został po raz pierwszy opisany przez Edmunda Hessa w 1876 roku. Jest wyjątkowy wśród regularnych związków, ponieważ nie ma regularnej wypukłej otoczki.
Jako gwiazda
Jest to druga gwiazda dwudziestościanu i podana jako indeks modelu Wenningera 23 .
Można go zbudować za pomocą rombowego triacontahedru z rombowymi piramidami dodanymi do wszystkich ścian, jak pokazano na pięciokolorowym obrazie modelu. (Ta konstrukcja nie generuje regularnego związku pięciu ośmiościanów, ale ma tę samą topologię i może być płynnie zdeformowana w regularny związek).
Ma gęstość większą niż 1.
| Diagram stellacyjny | Rdzeń stellacyjny | Wypukły kadłub |
|---|---|---|

|
 dwudziestościan |
 dwudziestościan |
Jako związek
Można go również postrzegać jako wielościenny związek pięciu ośmiościanów ułożonych w symetrię dwudziestościenną ( I h ).
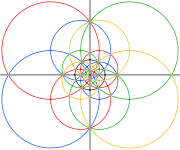
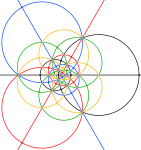
Sferyczne i stereograficzne projekcje tego związku wyglądają tak samo jak triacontahedron disdyakis . Ale wierzchołki wypukłej bryły na 3- i 5-krotnych osiach symetrii (szare na poniższych obrazkach) odpowiadają tylko skrzyżowaniom krawędzi w złożonym.
| Sferyczny wielościan | Projekcje stereograficzne | ||
|---|---|---|---|
| 2-krotnie | 3-krotnie | 5-krotny | |

|
|
|

|

|

|

|
|
| Obszar w czarnych kółkach poniżej odpowiada przedniej półkuli kulistego wielościanu. | |||
Zastąpienie ośmiościanów tetrahemiheksaedrami prowadzi do związku pięciu tetrahemiheksaedrów .
Inne związki 5-oktaedrowe
Istnieje również drugi związek 5-oktaedrowy z symetrią oktaedryczną. Można go wygenerować, dodając piąty ośmiościan do standardowego związku 4-oktaedrowego .
Zobacz też
- Związek trzech ośmiościanów
- Związek czterech ośmiościanów
- Związek dziesięciu ośmiościanów
- Związek dwudziestu ośmiościanów
- Peter R. Cromwell, Wielościany , Cambridge, 1997.
- Wenninger, Magnus (1974). Modele wielościanów . Wydawnictwo Uniwersytetu Cambridge. ISBN 0-521-09859-9 .
- Coxetera, Harolda Scotta MacDonalda ; Du Val, P.; Flather, HT; Petrie, JF (1999). Pięćdziesiąt dziewięć dwudziestościanów (wyd. 3). Tarquin. ISBN 978-1-899618-32-3 . MR 0676126 . (1st Edn University of Toronto (1938))
- HSM Coxeter , Regularne Polytopes , (wydanie 3, 1973), wydanie Dover, ISBN 0-486-61480-8 , 3.6 Pięć regularnych związków , pp.47-50, 6.2 Stellating the Platonic solids , pp.96-104
- E. Hess 1876 Zugleich Gleicheckigen und Gleichflächigen Polyeder , Schriften der Gesellschaft zur Berörderung der Gasammten Naturwissenschaften zu Marburg 11 (1876) s. 5–97.
Linki zewnętrzne
- MathWorld: ośmiościan 5-złożony
- Papierowy model złożony z pięciu ośmiościanów
- VRML : [1] [ stały martwy link ]
- Klitzing, Richard. „mieszanka 3D” .
| Godne uwagi stellacje dwudziestościanu | |||||||||
| Regularny | Jednolite dublety | Regularne związki | Zwykła gwiazda | Inni | |||||
| (Wypukły) dwudziestościan | Mały dwudziestościan triambiczny | Przyśrodkowy dwudziestościan triambiczny | Wielki dwudziestościan triambiczny | Związek pięciu ośmiościanów | Związek pięciu czworościanów | Związek dziesięciu czworościanów | Wielki dwudziestościan | Wykopany dwunastościan | Ostateczna stelacja |
|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

|
|

|

|

|

|

|

|

|

|

|
|
| Proces stellacji na dwudziestościanie tworzy szereg pokrewnych wielościanów i związków o symetrii dwudziestościanu . | |||||||||