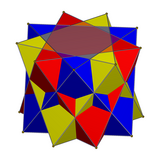
Związek trzech ośmiościanów
| Związek trzech ośmiościanów | |
|---|---|
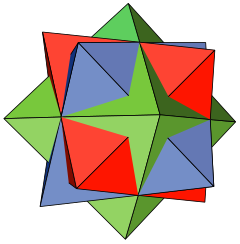
|
|
| Wielościany | 3 regularne ośmiościany |
| Twarze | 24 trójkąty równoboczne |
| Krawędzie | 36 |
| Wierzchołki | 18 |
|
Grupa symetrii (pojedynczy kolor) |
Och , zamów 48 |
W matematyce związek trzech ośmiościanów lub 3-związek ośmiościanu jest związkiem wielościennym utworzonym z trzech regularnych ośmiościanów , z których wszystkie mają wspólny środek, ale obracają się względem siebie. Chociaż pojawił się wcześniej w literaturze matematycznej, został ponownie odkryty i spopularyzowany przez MC Eschera , który użył go w centralnym obrazie swojego drzeworytu Stars z 1948 roku .
Budowa
Ośmiościan foremny można opisać wokół sześcianu w taki sposób, że osiem krawędzi dwóch przeciwległych kwadratów sześcianu leży na ośmiu ścianach ośmiościanu. Trzy ośmiościany utworzone w ten sposób z trzech par przeciwległych kwadratów sześciennych tworzą związek trzech ośmiościanów. Osiem wierzchołków sześcianu jest tym samym, co osiem punktów w układzie, w którym trzy krawędzie przecinają się. Każda z krawędzi ośmiościanu uczestnicząca w tych potrójnych przecięciach jest podzielona przez punkt przecięcia w stosunku 1: √ 2 . Pozostałe krawędzie ośmiościanu przecinają się parami, wewnątrz kompleksu; ich skrzyżowania znajdują się w ich punktach środkowych i tworzą kąty proste.
Złożenie trzech ośmiościanów można również utworzyć z trzech kopii pojedynczego ośmiościanu, obracając każdą kopię o kąt π /4 wokół jednej z trzech osi symetrii , które przechodzą przez dwa przeciwległe wierzchołki początkowego ośmiościanu. Trzecią konstrukcją dla tego samego związku trzech ośmiościanów jest podwójny wielościan związku trzech sześcianów , jeden z jednolitych związków wielościanów .
Sześć wierzchołków jednego z trzech ośmiościanów można określić za pomocą współrzędnych (0, 0, ±2) i (± √ 2 , ± √ 2 , 0) . Pozostałe dwa ośmiościany mają współrzędne, które można uzyskać z tych współrzędnych, zamieniając z na współrzędną x lub y .
Symetrie

Związek trzech ośmiościanów ma taką samą grupę symetrii jak pojedynczy ośmiościan. Jest to trójkąt izoedryczny , co oznacza, że jego ściany są trójkątami równobocznymi i ma symetrię polegającą na tym, że każda ściana łączy się z każdą inną ścianą. Istnieje jedna znana nieskończona rodzina deltaedrów izoedrycznych i 36 innych, które nie należą do tej rodziny; związek trzech ośmiościanów jest jednym z 36 sporadycznych przykładów. Jednak jego grupa symetrii nie przenosi każdego wierzchołka do każdego innego wierzchołka, więc sama w sobie nie jest jednolitym związkiem wielościanu.
Przecięcie trzech ośmiościanów to wypukły wielościan z 14 wierzchołkami i 24 ścianami, sześciościan tetrakisowy , utworzony przez dołączenie niskiej kwadratowej piramidy do każdej ściany centralnego sześcianu. Zatem związek można postrzegać jako gwiazdę sześciościanu tetrakis. Inna forma sześciościanu tetrakisa, utworzona przy użyciu wyższych piramid na każdej ścianie sześcianu, nie jest wypukła, ale ma ściany trójkąta równobocznego, które ponownie leżą na tych samych płaszczyznach, co ściany trzech ośmiościanów; jest to kolejny ze znanych deltaedrów izoedrycznych. Trzeci izoedryczny deltaedr dzielący te same płaszczyzny ścian, związek sześciu czworościanów , można utworzyć przez stellowanie każdej ściany związku trzech ośmiościanów, tworząc trzy stellae octagulae . Czwarty izoedryczny deltaedr z tymi samymi płaszczyznami ścian, również stellacja związku trzech ośmiościanów, ma taką samą kombinatoryczną strukturę jak sześciościan tetrakis, ale z powierzchniami sześcianu wgniecionymi do wewnątrz w przecinające się piramidy zamiast mocowania piramid na zewnątrz sześcianu .
Sześcian, wokół którego można opisać trzy ośmiościany, ma dziewięć płaszczyzn symetrii odbicia . Trzy z tych tafli refleksyjnych przechodzą równolegle do boków sześcianu, w połowie odległości między dwoma przeciwległymi bokami; pozostałe sześć przechodzi po przekątnej sześcianu przez cztery jego wierzchołki. Te dziewięć płaszczyzn pokrywa się z dziewięcioma płaszczyznami równikowymi trzech ośmiościanów.
Historia
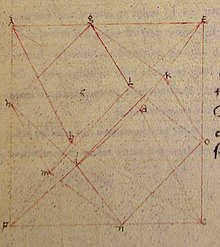
W XV-wiecznym rękopisie De quinque corporibus regularibus autorstwa Piero della Francesca , della Francesca zawiera już rysunek ośmiościanu opisanego wokół sześcianu, z ośmioma krawędziami sześcianu leżącymi na ośmiu ścianach ośmiościanu. Trzy ośmiościany opisane w ten sposób wokół pojedynczego sześcianu utworzyłyby związek trzech ośmiościanów, ale della Francesca nie przedstawia tego związku.
Kolejnym pojawieniem się związku trzech ośmiościanów w literaturze matematycznej wydaje się być praca Maxa Brücknera z 1900 roku , która wspomina o nim i zawiera fotografię jego modelu.
Holenderski artysta MC Escher w swoim drzeworycie Stars z 1948 roku użył jako centralnej figury drzeworytu klatki w tym kształcie, zawierającej dwa kameleony i unoszącej się w przestrzeni. HSM Coxeter , zakładając, że Escher odkrył ten kształt niezależnie, pisze: „To niezwykłe, że Escher, bez żadnej wiedzy z zakresu algebry lub geometrii analitycznej, był w stanie ponownie odkryć tę wysoce symetryczną figurę”. Jednak George W. Hart udokumentował, że Escher znał prace Brücknera i wykorzystał je jako podstawę dla wielu wielościanów gwiaździstych i związków wielościennych, które narysował. Wcześniej, w 1948 roku, Escher wykonał wstępny drzeworyt o podobnym temacie, Studium gwiazd , ale zamiast użyć w badaniu związku trzech regularnych ośmiościanów, użył innego, ale pokrewnego kształtu, gwiaździstego dwunastościanu rombowego (czasami nazywanego bryłą Eschera) , który można utworzyć jako związek trzech spłaszczonych ośmiościanów. Ta forma wielościanu jest topologicznie identyczna z dwunastościanem disdyakis , który można postrzegać jako dwunastościan rombowy z krótszymi piramidami na rombowych ścianach. Podwójna figura ośmiościennego związku, złożonego z trzech sześcianów, jest również pokazana na późniejszym drzeworycie Eschera, Wodospad , obok tego samego gwiaździstego dwunastościanu rombowego.
Złożenie trzech ośmiościanów ponownie weszło do literatury matematycznej w bardziej właściwy sposób dzięki pracy Bakosa i Johnsona (1959) , którzy zaobserwowali jego istnienie i dostarczyli współrzędne jego wierzchołków. Zostało to zbadane bardziej szczegółowo przez Wenningera (1968) i Coxetera (1985) .
Inne związki trzech ośmiościanów
Z ośmiościanami postrzeganymi jako trójkątne antygraniastosłupy , istnieje inny jednolity pryzmatyczny związek antygraniastosłupów o symetrii D 3d , rzędu 12. Każdy antygraniastosłup jest obrócony o 40 stopni. Widać, że górna i dolna płaszczyzna zawierają złożony enneagram , {9/3} lub 3{3}.
Zobacz też
- Związek czterech ośmiościanów
- Związek pięciu ośmiościanów
- Związek dziesięciu ośmiościanów
- Związek dwudziestu ośmiościanów