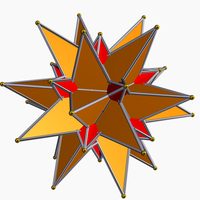
Związek dwudziestościanu wielkiego i dwunastościanu wielkiego gwiaździstego
| Związek dwudziestościanu wielkiego i dwunastościanu gwiaździstego | |
|---|---|
|
|
| Typ | gwiaździste i złożone |
| Diagram Coxetera |
|
| Wypukły kadłub | Dwunastościan |
| Wielościany |
1 dwudziestościan wielki 1 dwunastościan wielki gwiaździsty |
| Twarze |
20 trójkątów 12 pentagramów |
| Krawędzie | 60 |
| Wierzchołki | 32 |
| Grupa symetrii | dwudziestościenny ( I h ) |
Istnieją dwa różne związki dwudziestościanu wielkiego i dwudziestościanu wielkiego gwiaździstego : jeden jest związkiem podwójnym i stellacją dwudziestościanu wielkiego , a drugi jest stellacją dwudziestościanu dwudziestościanu .
Podwójny związek
Można go postrzegać jako wielościan składający się z dwudziestościanu wielkiego i dwunastościanu wielkiego gwiaździstego . Jest to jeden z pięciu związków zbudowanych z bryły platońskiej lub bryły Keplera-Poinsota i jej podwójny. Jest to gwiazdozbiór wielkiego dwudziestościanu .
Ma symetrię dwudziestościanu ( Ih ) i taki sam układ wierzchołków jak triacontahedr wielki rombowy .
Można to postrzegać jako jeden z dwóch trójwymiarowych odpowiedników związku dwóch pentagramów ({10/4} „ dekagram ”); ta seria jest kontynuowana w czwartym wymiarze jako związki gwiezdnych 4-polytopów .
Stelacja dwudziestościanu
Ten wielościan jest stelacją dwudziestościanu i podany jako indeks modelu Wenningera 61 . Ma taki sam układ wierzchołków jak rombowy triacontahedron , jego wypukła powłoka.
Aspekty stellacyjne dla konstrukcji to:
 Fasety z trójkąta |
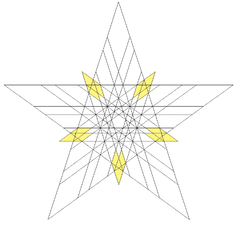 Fasety z pięciokąta |
Zobacz też
- Związek dwóch czworościanów
- Związek sześcianu i ośmiościanu
- Związek dwunastościanu i dwudziestościanu
- Związek małego dwunastościanu gwiaździstego i dwunastościanu wielkiego
- Wenninger, Magnus (1974). Modele wielościanów . Wydawnictwo Uniwersytetu Cambridge. ISBN 0-521-09859-9 . , P. 90.
- Wenninger, Magnus (1983). Modele dualne . Wydawnictwo Uniwersytetu Cambridge. ISBN 0-521-54325-8 . , s. 51-53.
- Martyn Cundy i A. Rollett. „Wielki dwudziestościan plus wielki dwunastościan gwiaździsty”. §3.10.4 w Modele matematyczne , wyd. Stradbroke, Anglia: Tarquin Pub., s. 132-133, 1989.





