Pięciokątny icositetrahedron

Pięciokątny icositetrahedron
(Kliknij w lewo* lub w prawo , aby wyświetlić modele obracające się).*
Typ	kataloński
Notacja Conwaya	gC
Diagram Coxetera
Wielokąt twarzy	nieregularny pięciokąt
Twarze	24
Krawędzie	60
Wierzchołki	38 = 6 + 8 + 24
Konfiguracja twarzy	V3.3.3.3.4
Kąt dwuścienny	136° 18' 33'
Grupa symetrii	O , ½BC ₃ , [4,3] ⁺ , 432
Podwójny wielościan	sześcian zadarty
Nieruchomości	wypukły , przechodni twarzowy , chiralny
Internet

Geometryczna konstrukcja stałej Tribonacciego (AC), z kompasem i zaznaczoną linijką, według metody opisanej przez Xerardo Neirę.

Model 3D pięciokątnego dwudziestościanu

W geometrii pięciokątny icositetrahedron lub pięciokątny icosikaitetrahedron jest bryłą katalońską , która jest podwójną kostką snub . W krystalografii jest również nazywany gyroidem .

Ma dwie różne formy, które są swoimi lustrzanymi odbiciami (lub „ enancjomorfami ”).

Budowa

Pięciokątny icositetrahedron można zbudować z zadartego sześcianu bez brania liczby podwójnej. Kwadratowe piramidy są dodawane do sześciu kwadratowych ścian sześcianu typu „snub”, a trójkątne piramidy są dodawane do ośmiu trójkątnych ścian, które nie mają wspólnej krawędzi z kwadratem. Wysokości piramid są dostosowywane tak, aby były współpłaszczyznowe z pozostałymi 24 trójkątnymi ścianami sześcianu. Rezultatem jest pięciokątny icositetrahedron.

współrzędne kartezjańskie

Oznacz stałą tribonacciego przez ${\ Displaystyle t \ około 1,839 \ 286 \, 755 \, 21}$ . (Zobacz sześcian zadarty , aby uzyskać geometryczne wyjaśnienie stałej tribonacciego). Wtedy współrzędne kartezjańskie dla 38 wierzchołków pięciokątnego dwudziestościanu wyśrodkowanego w początku są następujące:

12 parzystych permutacji (±1, ±(2t+1), ±t ² ) z parzystą liczbą znaków minus
12 nieparzystych permutacji (±1, ±(2t+1), ±t ² ) z nieparzystą liczbą znaków minus
6 punktów (±t ³ , 0, 0), (0, ±t ³ , 0) i (0, 0, ±t ³ )
8 punktów (±t ² , ±t ² , ±t ² )

Wypukłe łuski dla tych wierzchołków przeskalowane o $R$ o promieniu jednostkowym wyśrodkowany na początku, początku przeskalowany do i nieregularny chiralny sześcian zadarty w skali ${\ Displaystyle R \ około 0,9416969935}$ $\ Displaystyle R }$ , jak pokazano na poniższym rysunku:

Geometria

Pięciokątne ściany mają cztery kąty $}$ ${\ Displaystyle \ arccos (2-t)$ kąt . Pięciokąt ma trzy krótkie krawędzie o jednostkowej długości i dwie długie krawędzie o długości ${\ Displaystyle (t + 1) / 2 \ około 1,419 \, 643 \, 377 \ ,607\,08}$ . Kąt ostry leży między dwiema długimi krawędziami. Kąt dwuścienny równa się ${\ Displaystyle \ arccos (-1 / (t ^ {2} -2}) \ około 136,309 \ 232 \ 892 \ 32 ^ {\ circ}}$ .

Jeśli jego podwójny sześcian ma długość krawędzi jednostkową, to jego pole powierzchni i objętość wynoszą:

{\ Displaystyle {\ rozpocząć {wyrównane} A & = 3 {\ sqrt {\ Frac {22 (5t-1)}} {4t-3}}} & & \ około 19,299\,94\\V&={\sqrt {\frac {11(t-4)}{2(20t-37)}}}&&\około 7,4474\end{wyrównane}}}

Projekcje ortogonalne

Pięciokątny dwudziestościan ma trzy pozycje symetrii, dwie wyśrodkowane na wierzchołkach i jedną na środku krawędzi.

Projekcje ortogonalne
Symetria projekcyjna	[3]	[4] ⁺	[2]
Obraz
Podwójny obraz

Wariacje

izoedryczne o tej samej chiralnej symetrii oktaedrycznej można konstruować z pięciokątnymi ścianami mającymi 3 długości krawędzi.

Ta pokazana odmiana może być skonstruowana przez dodanie ostrosłupów do 6 kwadratowych ścian i 8 trójkątnych ścian sześcianu w taki sposób, że nowe trójkątne ściany z 3 współpłaszczyznowymi trójkątami połączyły się w identyczne pięciokątne ściany.

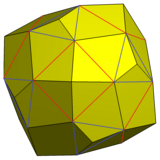Snub sześcian z powiększonymi piramidami i połączonymi ścianami	Pięciokątny icositetrahedron	Internet

Powiązane wielościany i tilings

Sferyczny pięciokątny icositetrahedron

Wielościan ten jest spokrewniony topologicznie jako część ciągu wielościanów i nachyleń pięciokątów z konfiguracjami ścian (V3.3.3.3. n ). (Sekwencja przechodzi w nachylenie płaszczyzny hiperbolicznej do dowolnego n .) Te figury przechodnie ścian mają (n32) symetrię obrotową .

n 32 mutacje symetrii snub tilings: 3.3.3.3.n
Symetria nr 32	Kulisty				euklidesowy	Kompaktowy hiperboliczny		parakomp.
Symetria nr 32	232	332	432	532	632	732	832	∞32
Zadarte figury
Konfig.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Figurki żyroskopowe
Konfig.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

Pięciokątny icositetrahedron jest drugim z serii podwójnych zadartych wielościanów i nachyleń z konfiguracją twarzy V3.3.4.3. rz .

4 n 2 mutacje symetrii zadanych nachyleń: 3.3.4.3.n
Symetria 4 n 2	Kulisty		euklidesowy	Kompaktowy hiperboliczny				parakomp.
Symetria 4 n 2	242	342	442	542	642	742	842	∞42
Zadarte figury
Konfig.	3.3.4.3.2	3.3.4.3.3	3.3.4.3.4	3.3.4.3.5	3.3.4.3.6	3.3.4.3.7	3.3.4.3.8	3.3.4.3.∞
Figurki żyroskopowe
Konfig.	V3.3.4.3.2	V3.3.4.3.3	V3.3.4.3.4	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	V3.3.4.3.8	V3.3.4.3.∞

Pięciokątny icositetrahedron jest jednym z rodziny podwójnych do jednolitych wielościanów związanych z sześcianem i regularnym ośmiościanem.

Jednolite wielościany ośmiościenne
Symetria : [4,3], (*432)							[4,3] ⁺ (432)	[1 ⁺ ,4,3] = [3,3] (*332)		[3 ⁺ ,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3 ^1,1 }	t{3,4} t{3 ^1,1 }	{3,4} {3 ^1,1 }	rr{4,3} s ₂ {3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h ₂ {4,3} t{3,3}	s{3,4} s{3 ^1,1 }

		=	=	=				= lub	= lub	=

Podwójne do jednolitych wielościanów
V4 ³	Wersja 3.8 ²	V(3.4) ²	V4.6 ²	V3 ⁴	wersja 3.4 ³	V4.6.8	V3 ⁴ .4	V3 ³	Wersja 3.6 ²	V3 ⁵

Williams, Robert (1979). Geometryczne podstawy naturalnej struktury: źródłowa księga projektowania . Dover Publications, Inc. ISBN 0-486-23729-X . (Sekcja 3-9)
Wenninger, Magnus (1983), Dual Models , Cambridge University Press , doi : 10.1017 / CBO9780511569371 , ISBN 978-0-521-54325-5 , MR 0730208 (Trzynaście półregularnych wypukłych wielościanów i ich liczby podwójne, strona 28, Pentagonal icositetrahedron)
Symetrie rzeczy 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss , ISBN 978-1-56881-220-5 [1] (Rozdział 21, Nazewnictwo wielościanów archimedesowych i katalońskich oraz nachylenia, strona 287, pięciokątny icosikaitetrahedron)

Linki zewnętrzne

Pentagonal Icositetrahedron – interaktywny model wielościanu