Trapez czworokątny
| Trapez czworokątny | |
|---|---|
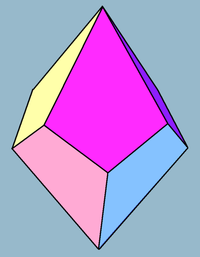 Kliknij na obrazek, aby zobaczyć go w powiększeniu. |
|
| Typ | trapezowy |
| Conway | dA4 |
| Diagram Coxetera |
|
| Twarze | 8 latawców |
| Krawędzie | 16 |
| Wierzchołki | 10 |
| Konfiguracja twarzy | V4.3.3.3 |
| Grupa symetrii | D 4d , [2 + ,8], (2*4), rząd 16 |
| Grupa rotacyjna | D 4 , [2,4] + , (224), rząd 8 |
| Podwójny wielościan | Kwadratowy antypryzmat |
| Nieruchomości | wypukła, przechodnia twarzy |
W geometrii czworokątny trapez lub deltohedron jest drugim w nieskończonej serii trapezów , które są podwójne do antygraniastosłupów . Ma osiem ścian, które są przystającymi latawcami i jest podwójny do kwadratowego antygraniastosłupa .
W generowaniu siatki
Ten kształt został użyty jako przypadek testowy do generowania siatki sześciennej , upraszczając wcześniejszy przypadek testowy zaproponowany przez matematyka Roberta Schneidersa w postaci kwadratowej piramidy z krawędzią podzieloną na 16 czworoboków. W tym kontekście czworokątny trapez był również nazywany sześciennym ośmiościanem , czworobocznym ośmiościanem lub ośmiokątnym wrzecionem , ponieważ ma osiem czworobocznych ścian i jest jednoznacznie zdefiniowany jako kombinatoryczny wielościan przez tę właściwość. Dodanie czterech prostopadłościanów do siatki ośmiościanu sześciennego dałoby również siatkę dla piramidy Schneidersa. Jako prosto połączony wielościan z parzystą liczbą czworobocznych ścian, sześcienny ośmiościan można rozłożyć na topologiczne prostopadłościany z zakrzywionymi ścianami, które stykają się twarzą w twarz bez podziału czworoboków granicznych, i wyraźna siatka tego typu została skonstruowana. Nie jest jednak jasne, czy można uzyskać rozkład tego typu, w którym wszystkie prostopadłościany są wypukłymi wielościanami o płaskich ścianach.
W sztuce
Czworościenny trapez pojawia się w lewym górnym rogu jako jedna z wielościennych „gwiazd” na drzeworycie Stars autorstwa MC Eschera z 1948 roku .
Płytki sferyczne
Czworościenny trapez występuje również jako sferyczna płytka z 2 wierzchołkami na biegunach i naprzemiennymi wierzchołkami równo rozmieszczonymi powyżej i poniżej równika.
Powiązane wielościany
| Nazwa trapezu |
Dwukątny trapez ( czworościan ) |
Trapez trójkątny | Trapez czworokątny | Trapez pięciokątny | Sześciokątny trapez | Siedmiokątny trapez | Ośmiokątny trapez | Dziesięciokątny trapez | Dwunastokątny trapez | ... | Apeirogonalny trapez |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Obraz wielościanu |

|
|

|

|

|

|

|

|

|
... | |
| obraz kafelkowy |
|

|

|

|

|

|

|

|

|
Obraz kafelkowy samolotu |
|
| Konfiguracja twarzy | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | Wersja 6.3.3.3 | Wersja 7.3.3.3 | Wersja 8.3.3.3 | V10.3.3.3 | Wersja 12.3.3.3 | ... | V∞.3.3.3 |
Tetragonalny trapez jest pierwszym z serii podwójnych wielościanów zadartych i nachyleń z konfiguracją twarzy V3.3.4.3. rz .
| 4 n 2 mutacje symetrii zadanych nachyleń: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
|
Symetria 4 n 2 |
Kulisty | euklidesowy | Kompaktowy hiperboliczny | parakomp. | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
|
Zadarte figury |

|

|

|

|

|

|

|

|
| Konfig. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| Figurki żyroskopowe |

|

|

|

|
||||
| Konfig. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
Linki zewnętrzne
