ośmiościan rombowy
| Ośmiościan rombowy | |
|---|---|
 (kliknij tutaj, aby zobaczyć model obrotowy) |
|
| Typ |
Bryła Archimedesa Jednolity wielościan |
| Elementy | F = 26, E = 48, V = 24 (χ = 2) |
| Twarze po bokach | 8{3}+(6+12){4} |
| Notacja Conwaya |
eC lub aaC aaaT |
| symbole Schläfliego | rr {4,3} lub |
| t 0,2 {4,3} | |
| Symbol Wythoffa | 3 4 | 2 |
| Diagram Coxetera |
|
| Grupa symetrii | O h , B 3 , [4,3], (*432), rząd 48 |
| Grupa rotacyjna | O , [4,3] + , (432), rząd 24 |
| Kąt dwuścienny |
3-4: 144°44′08″ (144,74°) 4-4: 135° |
| Bibliografia | U 10 , C 22 , W 13 |
| Nieruchomości | Półregularny wypukły |
 Kolorowe twarze |
 3.4.4.4 ( Rysunek wierzchołka ) |
 Dwudziestościan naramienny ( podwójny wielościan ) |
 Internet |
W geometrii ośmiościan rombowy lub mały ośmiościan rombowy lub rektyfikowany dwunastościan rombowy to wielościan z ośmioma trójkątnymi , sześcioma kwadratowymi i dwunastoma prostokątnymi ścianami. Istnieją 24 identyczne wierzchołki, z jednym trójkątem, jednym kwadratem i dwoma prostokątami spotykającymi się w każdym z nich. Jeśli wszystkie prostokąty same w sobie są kwadratowe (równoważnie, wszystkie krawędzie są tej samej długości, zapewniając trójkąty równoboczne ), jest to bryła Archimedesa . Wielościan ma symetrię ośmiościenną , podobnie jak sześcian i ośmiościan . Jego podwójny nazywa się icositetrahedronem naramiennym lub icositetrahedrem trapezoidalnym, chociaż jego ściany nie są tak naprawdę prawdziwymi trapezami .
Nazwy
Johannes Kepler w Harmonices Mundi (1618) nazwał ten wielościan ośmiościanem rombowym , będącym skrótem od ściętego rombu sześcienno-ośmiościennego , przy czym romb sześcienno-ośmiościanowy to jego nazwa dwunastościanu rombowego . Istnieją różne obcięcia dwunastościanu rombowego w topologiczny ośmiościan rombowy: wyraźnie jego rektyfikację (po lewej), tę, która tworzy jednolitą bryłę (w środku) oraz rektyfikację podwójnego ośmiościanu sześciennego (po prawej), która jest rdzeniem podwójny związek .
Można go również nazwać rozszerzonym lub kantelowanym sześcianem lub ośmiościanem , na podstawie operacji obcięcia na jednym z jednolitych wielościanów .
Od czasu włączenia go do Wings 3D jako „ośmiornica”, ten nieoficjalny przydomek rozprzestrzenia się.
Relacje geometryczne

Istnieją zniekształcenia ośmiościanu rombowego, które chociaż niektóre ściany nie są regularnymi wielokątami, nadal są jednolite w wierzchołkach. Niektóre z nich można wykonać, biorąc sześcian lub ośmiościan i odcinając krawędzie, a następnie przycinając rogi, tak aby powstały wielościan miał sześć kwadratowych i dwanaście prostokątnych ścian. Mają one symetrię ośmiościenną i tworzą ciągłą serię między sześcianem a ośmiościanem, analogicznie do zniekształceń rombozydodekahedru lub czworościennych zniekształceń sześciennego ośmiościanu . Jednak ośmiościan rombowy ma również drugi zestaw zniekształceń z sześcioma prostokątnymi i szesnastoma trapezowymi ścianami, które nie mają symetrii ośmiościennej, ale raczej symetrię T h , więc są niezmienne przy tych samych obrotach co czworościan , ale przy różnych odbiciach.
Linie, wzdłuż których można obracać kostkę Rubika , są rzutowane na kulę, podobną, topologicznie identyczną, do krawędzi ośmiościanu rombowego. W rzeczywistości wyprodukowano warianty wykorzystujące mechanizm kostki Rubika, które bardzo przypominają rombowy ośmiościan.
Ośmiościan rombowy jest używany w trzech jednorodnych teselacjach wypełniających przestrzeń : sześciennym plastrze miodu kantelowanym , sześciennym plastrze miodu ze ściętym ścięciem i naprzemiennym sześciennym plastrem miodu z runcinatem .
Sekcja
Ośmiościan rombowy można podzielić na dwie kwadratowe kopuły i środkowy ośmiokątny pryzmat . Obrót jednej kopuły o 45 stopni tworzy ośmiościan pseudorombowy <a i=6>. Oba te wielościany mają tę samą figurę wierzchołków: 3.4.4.4.
Istnieją trzy pary równoległych płaszczyzn, z których każda przecina ośmiościan rombowy w regularnym ośmiokącie. Ośmiościan rombowy można podzielić wzdłuż dowolnego z nich, aby uzyskać ośmiokątny pryzmat o regularnych ścianach i dwóch dodatkowych wielościanach zwanych kwadratowymi kopułami , które zaliczają się do brył Johnsona ; jest to zatem wydłużona kwadratowa orto bikupole . Kawałki te można ponownie złożyć, aby uzyskać nową bryłę zwaną wydłużoną kwadratową żyrobikupolą lub pseudorombowym ośmiościanem , z symetrią kwadratowego antygraniastosłupa. W tym przypadku wszystkie wierzchołki są lokalnie takie same jak wierzchołki ośmiościanu rombowego, z jednym trójkątem i trzema kwadratami spotykającymi się w każdym z nich, ale nie wszystkie są identyczne w odniesieniu do całego wielościanu, ponieważ niektóre są bliżej osi symetrii niż inne.

|
 Ośmiościan rombowy |
 Ośmiościan ośmiościan rombowy |
Projekcje ortogonalne
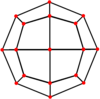
Ośmiościan rombowy ma sześć specjalnych rzutów ortogonalnych , wyśrodkowanych na wierzchołku, na dwóch rodzajach krawędzi i trzech typach ścian: trójkątach i dwóch kwadratach. Dwa ostatnie odpowiadają B2 i A2 Coxetera .
| Wyśrodkowany przez | Wierzchołek |
Krawędź 3-4 |
Krawędź 4-4 |
twarzy -1 |
twarzy -2 |
Trójkąt twarzy |
|---|---|---|---|---|---|---|
| Solidny |

|

|

|
|||
| szkielet |
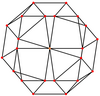
|

|

|
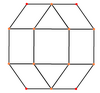
|

|

|
| Symetria projekcyjna |
[2] | [2] | [2] | [2] | [4] | [6] |
| Podwójny |
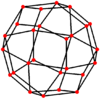
|

|
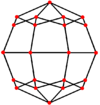
|

|
|

|
Płytki sferyczne
Ośmiościan rombowy można również przedstawić jako sferyczną płytkę i rzutować na płaszczyznę za pomocą rzutu stereograficznego . Ta projekcja jest konforemna , zachowując kąty, ale nie obszary lub długości. Linie proste na kuli są rzutowane na płaszczyznę jako okrągłe łuki.

|
 (6) wyśrodkowany w kwadracie |
 (6) wyśrodkowany w kwadracie |
 (8) wyśrodkowany w trójkącie |
| Projekcja ortogonalna | Projekcje stereograficzne | ||
|---|---|---|---|
Symetria pirytoedryczna
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Postać półsymetrii ośmiościanu rombowego istnieje z symetrią pirytoedryczną , [4,3 + ], (3*2) jako diagram Coxetera , symbol Schläfliego s 2 {3,4}, i można ją nazwać kantycznym ośmiościanem zadartym . Formę tę można zwizualizować, naprzemiennie kolorując krawędzie 6 kwadratów . Te kwadraty można następnie zniekształcić w prostokąty , podczas gdy 8 trójkątów pozostaje równobocznych. 12 przekątnych kwadratowych ścian stanie się trapezami równoramiennymi
Postać półsymetrii ośmiościanu rombowego istnieje z symetrią pirytoedryczną , [4,3 + ], (3*2) jako diagram Coxetera , symbol Schläfliego s 2 {3,4}, i można ją nazwać kantycznym ośmiościanem zadartym . Formę tę można zwizualizować, naprzemiennie kolorując krawędzie 6 kwadratów . Te kwadraty można następnie zniekształcić w prostokąty , podczas gdy 8 trójkątów pozostaje równobocznych. 12 przekątnych kwadratowych ścian stanie się trapezami równoramiennymi ![]()
![]()
![]()
![]()
![]() . W granicy prostokąty można zredukować do krawędzi, a trapezy stają się trójkątami i powstaje dwudziestościan przez zadarty ośmiościan , s {3,4}. ( Związek dwóch dwudziestościanów jest zbudowany z obu naprzemiennych pozycji).
. W granicy prostokąty można zredukować do krawędzi, a trapezy stają się trójkątami i powstaje dwudziestościan przez zadarty ośmiościan , s {3,4}. ( Związek dwóch dwudziestościanów jest zbudowany z obu naprzemiennych pozycji).
| Wariacje symetrii pirytoedrycznej | |||||||||
|---|---|---|---|---|---|---|---|---|---|
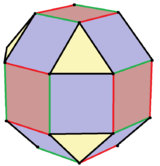 Jednolita geometria |
 Niejednolita geometria |
 Niejednolita geometria |
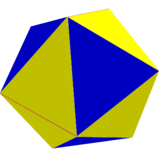 W limicie dwudziestościan zadarty ośmiościan , z jednej z dwóch pozycji. |
 Związek dwóch dwudziestościanów z obu naprzemiennych pozycji. |
|||||
Właściwości algebraiczne
współrzędne kartezjańskie
Współrzędne kartezjańskie wierzchołków ośmiościanu rombowego wyśrodkowanego w początku, o długości krawędzi równej 2 jednostkom, są parzystymi permutacjami
- (±1, ±1, ±(1 + √ 2 )).
Jeśli oryginalny rombowy ośmiościan ma jednostkową długość krawędzi, jego podwójny stromiczny dwudziestościan ma długości krawędzi
Powierzchnia i objętość
Pole A i objętość V ośmiościanu rombowego o długości krawędzi a wynoszą:
Gęstość upakowania bliskiego
Optymalna frakcja upakowania rombicuboctaedrów jest podana przez
- .
Zauważono, że tę optymalną wartość uzyskuje w sieci Bravais de Graaf ( 2011 ). Ponieważ ośmiościan rombowy jest zawarty w dwunastościanie rombowym , którego wpisana kula jest identyczna z jego własną wpisaną kulą, wartość optymalnego ułamka upakowania jest następstwem hipotezy Keplera : można to osiągnąć, umieszczając ośmiościan rombowy w każdej komórce dwunastościanu rombowego plaster miodu i nie można go przekroczyć, ponieważ w przeciwnym razie optymalna gęstość upakowania kul mogłaby zostać przekroczona przez umieszczenie kuli w każdym ośmiościanie rombowym hipotetycznego upakowania, które ją przekracza.
w sztuce
Portret Luca Pacioli z 1495 roku , tradycyjnie przypisywany Jacopo de' Barbari , zawiera szklany rombowy ośmiościan wypełniony do połowy wodą, który mógł być namalowany przez Leonarda da Vinci . Pierwsza drukowana wersja ośmiościanu rombowego została napisana przez Leonarda i pojawiła się w dziele Pacioli 's Divina ratione (1509).
Sferyczna panorama 180° × 360° może być rzutowana na dowolny wielościan; ale ośmiościan rombowy zapewnia wystarczająco dobre przybliżenie kuli, a jednocześnie jest łatwy do zbudowania. Ten typ projekcji, zwany Filosferą , jest możliwy w niektórych programach do montażu panoram. Składa się z dwóch obrazów, które są drukowane oddzielnie i cięte nożyczkami, pozostawiając kilka klapek do złożenia za pomocą kleju.
Obiekty
Gry Freescape Driller i Dark Side miały mapę gry w postaci ośmiościanu rombowego .
„Hurry-Scurry Galaxy” i „Sea Slide Galaxy” w grze wideo Super Mario Galaxy mają planety o podobnym kształcie ośmiościanu rombu.
Sonic the Hedgehog 3 ' s Icecap Zone ma filary zwieńczone rombicuboctahedrami.
Podczas szaleństwa na kostki Rubika w latach 80. co najmniej dwie sprzedawane kręte układanki miały kształt ośmiościanu rombowego (mechanizm był podobny do mechanizmu kostki Rubika ) .
Powiązane wielościany
Rombowy ośmiościan należy do rodziny jednolitych wielościanów związanych z sześcianem i regularnym ośmiościanem.
| Jednolite wielościany ośmiościenne | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symetria : [4,3], (*432) |
[4,3] + (432) |
[1 + ,4,3] = [3,3] (*332) |
[3 + ,4] (3*2) |
|||||||
| {4,3} | t{4,3} |
r{4,3} r{3 1,1 } |
t{3,4} t{3 1,1 } |
{3,4} {3 1,1 } |
rr{4,3} s 2 {3,4} |
tr{4,3} | sr{4,3} |
h{4,3} {3,3} |
h 2 {4,3} t{3,3} |
s{3,4} s{3 1,1 } |
|
|
|
|
|
|
|
|
|
|
||
|
= |
= |
= |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
| Podwójne do jednolitych wielościanów | ||||||||||
| V4 3 | Wersja 3.8 2 | V(3.4) 2 | V4.6 2 | V3 4 | wersja 3.4 3 | V4.6.8 | V3 4 .4 | V3 3 | Wersja 3.6 2 | V3 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Mutacje symetrii
Ten wielościan jest powiązany topologicznie jako część ciągu kantelowanych wielościanów z figurą wierzchołków (3.4.n.4 ) i kontynuuje jako nachylenie płaszczyzny hiperbolicznej . Te przechodnie wierzchołków mają (* n 32) symetrię odbiciową .
| * n 32 mutacja symetrii rozwiniętych nachyleń: 3.4. nr 4 | ||||||||
|---|---|---|---|---|---|---|---|---|
|
Symetria * n 32 [n,3] |
Kulisty | Euklides. | Kompaktowy hiperb. | parakomp. | ||||
|
*232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
|
| Postać |
|

|

|

|

|

|

|

|
| Konfig. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
| * n 42 mutacja symetrii rozszerzonych nachyleń: n .4.4.4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
Symetria [n,4], (* n 42) |
Kulisty | euklidesowy | Kompaktowy hiperboliczny | parakomp. | |||||||
|
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4] |
*∞42 [∞,4] |
|||||
|
Rozbudowane figury |

|

|

|

|

|

|

|
||||
| Konfig. | 3.4.4.4 | 4.4.4.4 | 5.4.4.4 | 6.4.4.4 | 7.4.4.4 | 8.4.4.4 | ∞.4.4.4 | ||||
|
figur rombowych . |
 V3.4.4.4 |
 V4.4.4.4 |
 V5.4.4.4 |
 Wersja 6.4.4.4 |
 V7.4.4.4 |
 Wersja 8.4.4.4 |
 V∞.4.4.4 |
||||
Układ wierzchołków
Dzieli swój układ wierzchołków z trzema niewypukłymi jednorodnymi wielościanami : gwiaździstym ściętym sześciościanem , małym rombosześcianem (mający wspólne trójkątne ściany i sześć kwadratowych ścian) oraz małym ośmiościanem sześciennym (mający dwanaście wspólnych kwadratowych ścian).
 ośmiościan rombowy |
 Mały ośmiościan sześcienny |
 Mały rombsześcian |
 Gwiaździsty ścięty sześciościan |
| Wykres rombowy sześcienno-oktaedryczny | |
|---|---|
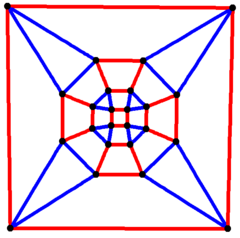 4-krotna symetria
| |
| Wierzchołki | 24 |
| Krawędzie | 48 |
| Automorfizmy | 48 |
| Nieruchomości | Graf kwartalny , hamiltonian , regularny |
| Tabela wykresów i parametrów | |
Wykres rombowo-ośmiościenny
Graf rombowo-ośmiościanu to wykres wierzchołków i krawędzi ośmiościanu rombu. Ma 24 wierzchołki i 48 krawędzi i jest kwartalnym grafem Archimedesa .
Zobacz też
- Związek pięciu rombicuboctaedrów
- Sześcian
- sześcienny ośmiościan
- Niewypukły wielki ośmiościan rombowy
- Ścięty ośmiościan rombowy
- Wydłużona kwadratowa gyrobicupola
- Morawska gwiazda
- Oktaedr
- rombozydodziesięciościan
- Rubik's Snake - łamigłówka, która może uformować „kulę” romboośmiościanu
- Białoruska Biblioteka Narodowa – jej główny element architektoniczny ma kształt ośmiościanu rombowego.
- Ścięty ośmiościan ośmiościan (wielki ośmiościan rombowy)
Dalsza lektura
- Williams, Robert (1979). Geometryczne podstawy naturalnej struktury: źródłowa księga projektowania . Dover Publications, Inc. ISBN 0-486-23729-X . (sekcja 3–9)
- Cromwell, P. (1997). Wielościany . Wielka Brytania: Cambridge. s. 79–86 Bryły Archimedesa . ISBN 0-521-55432-2 .
- Coxeter, HSM ; Longuet-Higgins, MS; Miller, JCP (13 maja 1954). „Jednolite wielościany”. Transakcje filozoficzne Royal Society of London. Seria A, nauki matematyczne i fizyczne . 246 (916): 401–450. Bibcode : 1954RSPTA.246..401C . doi : 10.1098/rsta.1954.0003 . S2CID 202575183 .
- de Graaf, J.; van Roij, R.; Dijkstra, M. (2011), „Gęste regularne opakowania nieregularnych cząstek niewypukłych”, Physical Review Letters , 107 (15): 155501, arXiv : 1107,0603 , Bibcode : 2011PhRvL.107o5501D , doi : 10.1103/PhysRevLett.107.1 55501 , PMID 22107298 , S2CID 14041658
- Betke, U.; Henk, M. (2000), „Najgęstsze opakowania kratowe 3-Polytopes”, Computational Geometry , 16 (3): 157–186, arXiv : math / 9909172 , doi : 10,1016 / S0925-7721 (00) 00007-9
- Torquato, S.; Jiao, Y. (2009), „Gęste upakowania brył platońskich i archimedesowych”, Nature , 460 (7257): 876–879, arXiv : 0908,4107 , Bibcode : 2009Natur.460..876T , doi : 10.1038/nature08239 , PMID 19675649 , S2CID 52819935
- Hales, Thomas C. (2005), „Dowód hipotezy Keplera” , Annals of Mathematics , 162 (3): 1065–1185, arXiv : math / 9811078v2 , doi : 10.4007 / annals.2005.162.1065
Linki zewnętrzne
- Eric W. Weisstein , Rhombicuboctahedron ( bryła Archimedesa ) w MathWorld .
- Klitzing, Richard. „3D wypukłe jednolite wielościany x3o4x - sirco” .
- Jednolite wielościany
- Wielościany wirtualnej rzeczywistości Encyklopedia wielościanów
- Edytowalna siatka ośmiościanu rombowego do druku z interaktywnym widokiem 3D
- Gwiazda ośmiościanu rombowego autorstwa Sándora Kabai, Wolfram Demonstrations Project .
- Ośmiościan rombowy: paski papieru do wyplatania










































































