Plaster miodu (geometria)

W geometrii plaster miodu to wypełnienie przestrzeni lub ścisłe upakowanie wielościennych lub wielowymiarowych komórek , tak aby nie było żadnych przerw. Jest to przykład bardziej ogólnego kafelkowania matematycznego lub teselacji w dowolnej liczbie wymiarów. Jego wymiar można przedstawić jako n -plaster miodu dla plastra miodu o n -wymiarowej przestrzeni.

Plastry miodu są zwykle budowane w zwykłej przestrzeni euklidesowej („płaskiej”). Mogą być również konstruowane w przestrzeniach nieeuklidesowych , takich jak hiperboliczne plastry miodu . Dowolny skończony jednorodny polytope można rzutować na jego obwód , aby utworzyć jednolity plaster miodu w przestrzeni sferycznej.

Możliwe jest wypełnienie płaszczyzny wielokątami , które nie stykają się w rogach, na przykład za pomocą prostokątów , jak we wzorze ściany z cegły : nie jest to prawidłowe układanie płytek, ponieważ narożniki leżą częściowo wzdłuż krawędzi sąsiedniego wielokąta. Podobnie we właściwym plastrze miodu nie może być żadnych krawędzi ani wierzchołków leżących częściowo wzdłuż powierzchni sąsiedniej komórki. Interpretacja każdej ściany cegły jako sześciokąta mającego dwa kąty wewnętrzne po 180 stopni pozwala uznać wzór za właściwą płytkę. Jednak nie wszyscy geometrzy akceptują takie sześciokąty.

Klasyfikacja

Istnieje nieskończenie wiele plastrów miodu, które zostały tylko częściowo sklasyfikowane. Największe zainteresowanie wzbudziły te bardziej regularne, podczas gdy wciąż odkrywany jest bogaty i różnorodny asortyment innych.

Najprostsze do zbudowania plastry miodu są uformowane z ułożonych w stos warstw lub płyt graniastosłupów opartych na niektórych teselacjach płaszczyzny. W szczególności dla każdego równoległościanu kopie mogą wypełnić przestrzeń, przy czym sześcienny plaster miodu jest wyjątkowy, ponieważ jest to jedyny regularny plaster miodu w zwykłej (euklidesowej) przestrzeni. Inną interesującą rodziną są czworościany Hilla i ich uogólnienia, które mogą również układać się w przestrzeni.

Jednolite 3 plastry miodu

Trójwymiarowy jednorodny plaster miodu to plaster miodu w 3-przestrzeni złożony z jednolitych komórek wielościennych i mający wszystkie wierzchołki takie same (tj. Grupa [izometrii 3-przestrzeni, która zachowuje kafelkowanie] jest przechodnia na wierzchołkach ). Istnieje 28 wypukłych przykładów w euklidesowej przestrzeni 3, zwanych także Archimedesowymi plastrami miodu .

Plaster miodu nazywamy regularnym , jeśli grupa izometrii zachowująca kafelki działa przechodnie na flagi, gdzie flaga jest wierzchołkiem leżącym na krawędzi leżącej na ścianie leżącej na komórce. Każdy zwykły plaster miodu jest automatycznie jednolity. Jednak w trójwymiarowej przestrzeni euklidesowej jest tylko jeden regularny plaster miodu, sześcienny plaster miodu . Dwa są quasiregularne (wykonane z dwóch rodzajów regularnych komórek):

Typ	Zwykły sześcienny plaster miodu	Quasiregularne plastry miodu
Komórki	Sześcienny	Oktaedry i czworościany
Warstwa płyty

Czworościenno -ośmiościenny plaster miodu i zawirowane czworościenno-ośmiościenne plastry miodu są generowane przez 3 lub 2 pozycje warstwy płytowej komórek, z których każda jest naprzemiennie czworościanami i ośmiościanami. Nieskończona liczba unikalnych plastrów miodu może zostać utworzona przez wyższe uporządkowanie wzorów powtarzających się warstw tych płyt.

Wypełniające przestrzeń wielościany

Mówi się, że plaster miodu, w którym wszystkie komórki są identyczne w obrębie jego symetrii, jest przechodni przez komórki lub izochoryczny . Mówi się, że w trójwymiarowej przestrzeni euklidesowej komórka takiego plastra miodu jest wypełniającym przestrzeń wielościanem . Warunkiem koniecznym , aby wielościan był wielościanem wypełniającym przestrzeń, jest to, że jego niezmiennik Dehna musi wynosić zero, wykluczając jakąkolwiek bryłę platońską inną niż sześcian.

Pięć wypełniających przestrzeń wielościanów może teselować trójwymiarową przestrzeń euklidesową tylko przy użyciu translacji. Nazywa się je równoległościanami :

Sześcienny plaster miodu (lub odmiany: prostopadłościan , sześcian rombowy lub równoległościan )
Sześciokątny pryzmatyczny plaster miodu
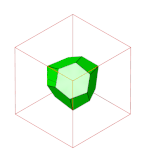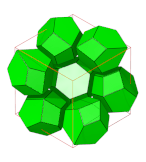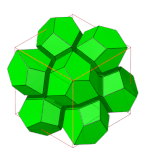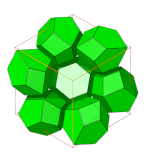
Rombowy dwunastościenny plaster miodu
Wydłużony dwunastościenny plaster miodu
Bitruncated sześcienny plaster miodu lub ścięte ośmiościany

Sześcian (równoległościan)	Sześciokątny pryzmat	dwunastościan rombowy	Wydłużony dwunastościan	Ścięty ośmiościan
sześcienny plaster miodu	Sześciokątny pryzmatyczny plaster miodu	dwunastościany rombowe	Wydłużone dwunastościany	Ścięte ośmiościany

3 długości krawędzi	3+1 długości krawędzi	4 długości krawędzi	4+1 długości krawędzi	6 długości krawędzi

Inne znane przykłady wielościanów wypełniających przestrzeń to:

Trójkątny pryzmatyczny plaster miodu
Zawirowany trójkątny pryzmatyczny plaster miodu
Triakis obcięty czworościenny plaster miodu . Taki kształt mają komórki Woronoja atomów węgla w diamencie.
Trapezorombowy dwunastościenny plaster miodu
Nachylenia izoedryczne

Inne plastry miodu z dwoma lub więcej wielościanami

Czasami dwa lub więcej różnych wielościanów można połączyć, aby wypełnić przestrzeń. Oprócz wielu jednolitych plastrów miodu, innym dobrze znanym przykładem jest struktura Weaire-Phelana , przejęta ze struktury kryształów hydratu klatratu

Okresowa jednostka struktury Weaire-Phelana .

P8 tiling (with left and right-handed cells)

Plaster miodu według leworęcznych i praworęcznych wersji tego samego wielościanu.

Niewypukłe 3-plastry miodu

Udokumentowane przykłady są rzadkie. Można wyróżnić dwie klasy:

Niewypukłe komórki, które pakują się bez nakładania się, analogicznie do nachyleń wklęsłych wielokątów. Należą do nich upakowanie małego gwiaździstego dwunastościanu rombowego , jak w kostce Yoshimoto .
Nakładanie się komórek, których dodatnie i ujemne gęstości „znoszą się”, tworząc jednolicie gęste kontinuum, analogiczne do zachodzących na siebie nachyleń płaszczyzny.

Hiperboliczne plastry miodu

W trójwymiarowej przestrzeni hiperbolicznej kąt dwuścienny wielościanu zależy od jego wielkości. Regularne hiperboliczne plastry miodu obejmują zatem dwa z czterema lub pięcioma dwunastościanami spotykającymi się na każdej krawędzi; ich kąty dwuścienne wynoszą zatem π/2 i 2π/5, z których oba są mniejsze niż kąt dwunastościanu euklidesowego. Oprócz tego efektu hiperboliczne plastry miodu podlegają tym samym ograniczeniom topologicznym, co plastry euklidesowe i polichora.

Wyliczono 4 zwarte i 11 parazwartych regularnych hiperbolicznych plastrów miodu oraz wiele zwartych i parazwartych jednorodnych hiperbolicznych plastrów miodu.

Cztery regularne kompaktowe plastry miodu w H ³
{5,3,4}	{4,3,5}	{3,5,3}	{5,3,5}

11 parakompaktowych zwykłych plastrów miodu
{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{4,4,3}	{4,4,4}
{3,3,6}	{4,3,6}	{5,3,6}	{3,6,3}	{3,4,4}

Dualność 3-plastrów miodu

Na każdy plaster miodu przypada podwójny plaster miodu, który można otrzymać wymieniając:

komórki dla wierzchołków.

twarze dla krawędzi.

To są tylko zasady dualizacji czterowymiarowych 4-polytopów , z wyjątkiem tego, że zwykła skończona metoda odwrotności wokół koncentrycznej hipersfery może napotkać problemy.

Bardziej regularne plastry miodu zgrabnie podwajają się:

Sześcienny plaster miodu jest samopodwójny.
To ośmiościanów i czworościanów jest podwójne do rombowych dwunastościanów.
Plastry miodu płytowe pochodzące z jednolitych płytek płaskich są względem siebie podwójne w taki sam sposób, jak płytki.
Wszystkie dublety pozostałych plastrów Archimedesa są przechodnie przez komórki i zostały opisane przez Inchbalda.

Samopodwójne plastry miodu

Plastry miodu mogą być również samodualne . Wszystkie n -wymiarowe hipersześcienne plastry miodu z symbolami Schläfliego {4,3 ^{n −2,4} } są samodualne.

Zobacz też

Dalsza lektura

Coxeter, HSM : Regularne Polytopy .
Williams, Robert (1979). Geometryczne podstawy naturalnej struktury: źródłowa księga projektowania . Dover Publications, Inc., s. 164–199. ISBN 0-486-23729-X . Rozdział 5: Pakowanie wielościanów i wypełnianie przestrzeni
Critchlow K.: Porządek w przestrzeni .
Pearce, Struktura w naturze jest strategią projektowania .
Goldberg, Michael Trzy nieskończone rodziny czworościennych wypełniaczy przestrzeni Journal of Combinatorial Theory A, 16, s. 348–354, 1974.
Goldberg, Michael (1972). „Pięciościany wypełniające przestrzeń” . Dziennik teorii kombinatorycznej, seria A. 13 (3): 437–443. doi : 10.1016/0097-3165(72)90077-5 .
Goldberg, Michael The Space-filling Pentahedra II , Journal of Combinatorial Theory 17 (1974), 375–378.
Goldberg, Michael (1977). „Na wypełniających przestrzeń sześcianach”. Geometria dedykowana . 6 . doi : 10.1007/BF00181585 . S2CID 189889869 .
Goldberg, Michael (1978). „Na wypełniających przestrzeń heptaedrach”. Geometria dedykowana . 7 (2): 175–184. doi : 10.1007/BF00181630 . S2CID 120562040 .
Goldberg, Michael Wypukłe wielościenne wypełniacze przestrzeni o więcej niż dwunastu twarzach. Geom. Dedicata 8, 491-500, 1979.
Goldberg, Michael (1981). „O ośmiościanach wypełniających przestrzeń” . Geometria dedykowana . 10 (1–4): 323–335. doi : 10.1007/BF01447431 . S2CID 189876836 .
Goldberg, Michael (1982). „O dziesięciościanach wypełniających przestrzeń” . {{ cite journal }} : Cite journal wymaga |journal= ( pomoc )
Goldberg, Michael (1982). „O enneahedrach wypełniających przestrzeń”. Geometria dedykowana . 12 (3). doi : 10.1007/BF00147314 . S2CID 120914105 .

Linki zewnętrzne

Olszewski, Jerzy. „Plaster miodu” . Glosariusz hiperprzestrzeni . Zarchiwizowane od oryginału w dniu 4 lutego 2007 r.
Pięć wypełniających przestrzeń wielościanów , Guy Inchbald, The Mathematical Gazette 80 , listopad 1996, s. 466-475.
Raumfueller (Wielościany wypełniające przestrzeń) autorstwa TE Dorozinskiego
Weisstein, Eric W. „Wielościan wypełniający przestrzeń” . MathWorld .

Podstawowe wypukłe regularne i jednolite plastry miodu w wymiarach 2–9
Przestrzeń	Rodzina	${\ Displaystyle {\ tylda {A}} _ {n-1}}$	${\ Displaystyle {\ tylda {C}} _ {n-1}}$	${\ Displaystyle {\ tylda {B}} _ {n-1}}$	${\ Displaystyle {\ tylda {D}} _ {n-1}}$	${\ Displaystyle {\ tylda {G}} _ {2}}$ / ${\ Displaystyle {\ tylda {F}} _ {4}}$ / ${\ Displaystyle {\ tylda { E}}_{n-1}}$
E ²	Jednolita płytka	{3 ^[3] }	δ ₃	hδ ₃	qδ ₃	Sześciokątny
E ³	Jednolity wypukły plaster miodu	{3 ^[4] }	δ ₄	hδ ₄	qδ ₄
E ⁴	Jednolity 4-plaster miodu	{3 ^[5] }	δ ₅	hδ ₅	qδ ₅	24-komorowy plaster miodu
E5 ^_	Jednolity 5-plaster miodu	{3 ^[6] }	δ ₆	hδ ₆	qδ ₆
E6 ^_	Jednolity 6-plaster miodu	{3 ^[7] }	δ ₇	hδ ₇	qδ ₇	2 ₂₂
E7 ^_	Jednolity 7-plaster miodu	{3 ^[8] }	δ ₈	hδ ₈	qδ ₈	1 ₃₃ • 3 ₃₁
E ⁸	Jednolity 8-plaster miodu	{3 ^[9] }	δ ₉	hδ ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
E ⁹	Jednolity 9-plaster miodu	{3 ^[10] }	δ ₁₀	hδ ₁₀	qδ ₁₀
E ¹⁰	Mundur 10-plaster miodu	{3 ^[11] }	δ ₁₁	hδ ₁₁	qδ ₁₁
E ^{n -1}	Mundur ( n -1)- plaster miodu	{3 ^[n] }	δ _rz	hδ _rz	qδ _rz	1 _k2 • 2 _k1 • k ₂₁