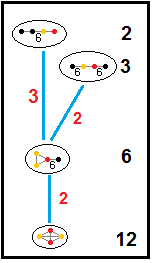
Trójkątny plaster miodu do płytek

Trójkątny plaster miodu do płytek
Typ	Hiperboliczny zwykły plaster miodu Parakompaktowy jednolity plaster miodu
Symbol Schläfliego	{3,6,3} godz.{6,3,6} godz.{6,3 [3] } ↔ {3 [3,3] }
Diagramy Coxetera-Dynkina	↔ ↔ ↔
Komórki	{3,6}
Twarze	trójkąt {3}
Rysunek krawędzi	trójkąt {3}
figura wierzchołka	płytki sześciokątne
Podwójny	Samopodwójny
grupy Coxetera	${\ Displaystyle {\ overline {Y}} _ {3}}$ , [3,6,3] ${\ Displaystyle {\ overline {VP}} _ {3}}$ , [6,3 [3] ] ${\ Displaystyle {\ overline {PP}} _ {3}}$ [3 [3,3] ]
Nieruchomości	Regularny

Trójkątny plaster miodu z płytek jest jednym z 11 parazwartych regularnych teselacji wypełniających przestrzeń (lub plastrów miodu ) w hiperbolicznej 3-przestrzeni . Nazywa się to parazwartością , ponieważ ma nieskończone komórki i figury wierzchołków , przy czym wszystkie wierzchołki są idealnymi punktami w nieskończoności. Ma symbol Schläfliego {3,6,3} i składa się z trójkątnych płytek komórki. Każda krawędź plastra miodu jest otoczona trzema komórkami, a każdy wierzchołek jest idealny, gdy spotyka się tam nieskończenie wiele komórek. Jego figura wierzchołka to sześciokątne kafelki .

Geometryczny plaster miodu to wypełnienie przestrzeni wielościennymi lub wielowymiarowymi komórkami , dzięki czemu nie ma luk . Jest to przykład bardziej ogólnego kafelkowania matematycznego lub teselacji w dowolnej liczbie wymiarów.

Plastry miodu są zwykle budowane w zwykłej przestrzeni euklidesowej („płaskiej”), podobnie jak wypukłe jednolite plastry miodu . Mogą być również konstruowane w przestrzeniach nieeuklidesowych , takich jak hiperboliczne jednolite plastry miodu . Dowolny skończony jednorodny polytope można rzutować na jego obwód , aby utworzyć jednolity plaster miodu w przestrzeni sferycznej.

Symetria

Podgrupy [3,6,3] i [6,3,6]

Ma dwie konstrukcje o niższej symetrii odblaskowej, jako naprzemienny porządek - 6 sześciokątnych płytek o strukturze plastra miodu , ↔ i od , który naprzemiennie 3 rodzaje (kolory) trójkątnych płytek wokół każdej krawędzi. W notacji Coxetera usunięcie trzeciego i czwartego lustra [3,6,3 ^* ] tworzy nową grupę Coxetera [3 ^[3,3] ], , indeks podgrupy 6. Dziedzina podstawowa jest 6 razy większa. Według diagramu Coxetera istnieją 3 kopie pierwszego oryginalnego lustra w nowej domenie podstawowej: ↔ .

Powiązane kafelki

Jest podobny do hiperbolicznego kafelkowania apeirogonalnego 2D nieskończonego rzędu , {∞, ∞}, z nieskończonymi apeirogonalnymi ścianami i wszystkimi wierzchołkami na idealnej powierzchni.

Powiązane plastry miodu

Trójkątny plaster miodu z płytkami jest regularnym hiperbolicznym plastrem miodu w przestrzeni 3 i jednym z jedenastu parakompaktowych plastrów miodu.

Istnieje dziewięć jednolitych plastrów miodu w rodzinie [3,6,3] grupy Coxeter , w tym ta regularna forma, jak również forma bitruncated , t _1,2 {3,6,3}, ze wszystkimi ściętymi sześciokątnymi ścianami płytek.

[3,6,3] rodzinne plastry miodu

{3,6,3}	r{3,6,3}	t{3,6,3}	rrr{3,6,3}	t 0,3 {3,6,3}	2t{3,6,3}	tr{3,6,3}	t 0,1,3 {3,6,3}	t 0,1,2,3 {3,6,3}

Plaster miodu jest również częścią serii polychora i plastrów miodu z trójkątnymi figurami krawędziowymi .

{3, p ,3} polytopy
Przestrzeń	S 3		H 3
Formularz	Skończone		Kompaktowy	Parakompaktowy	Niekompaktowy
{3, str . 3}	{3,3,3}	{3,4,3}	{3,5,3}	{3,6,3}	{3,7,3}	{3,8,3}	... {3,∞,3}
Obraz
Komórki	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}
figura wierzchołka	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Rektyfikowany trójkątny plaster miodu z płytek

Rektyfikowany trójkątny plaster miodu z płytek
Typ	Parakompaktowy jednolity plaster miodu
Symbol Schläfliego	r{3,6,3} h 2 {6,3,6}
Diagram Coxetera	↔ ↔ ↔
Komórki	r{3,6} {6,3}
Twarze	trójkąt {3} sześciokąt {6}
figura wierzchołka	trójkątny pryzmat
zespół Coxetera	${\ Displaystyle {\ overline {Y}} _ {3}}$ , [3,6,3] ${\ Displaystyle {\ overline {VP}} _ {3}}$ , [6,3 [3] ] ${\ Displaystyle {\ overline {PP}} _ {3}}$ [3 [3,3] ]
Nieruchomości	Przechodnie wierzchołków, przechodnie krawędzi

Rektyfikowany trójkątny plaster miodu z płytkami ma trójkątne płytki i sześciokątne płytki z komórkami z trójkątną figurą wierzchołka graniastosłupa.

Symetria

Niższa symetria tego plastra miodu może być skonstruowana jako kantyczny porządek - 6 sześciokątnych płytek plastra miodu , ↔ . Drugą konstrukcją o niższym indeksie jest ↔ .

Ścięty trójkątny dachówka o strukturze plastra miodu

Ścięty trójkątny dachówka o strukturze plastra miodu
Typ	Parakompaktowy jednolity plaster miodu
Symbol Schläfliego	t{3,6,3}
Diagram Coxetera
Komórki	t{3,6} {6,3}
Twarze	sześciokąt {6}
figura wierzchołka	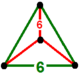czworościan
zespół Coxetera	${\ Displaystyle {\ overline {Y}} _ {3}}$ , [3,6,3] ${\ Displaystyle {\ overline {V}} _ {3}}$ , [3,3, 6]
Nieruchomości	Regularny

Ścięty trójkątny plaster miodu z płytkami , , jest formą o niższej symetrii sześciokątnego plastra miodu z płytek , . Zawiera sześciokątne ścianki płytek z czworościenną figurą wierzchołków.

Trójkątny plaster miodu z bitruncated

Trójkątny plaster miodu z bitruncated
Typ	Parakompaktowy jednolity plaster miodu
Symbol Schläfliego	2t{3,6,3}
Diagram Coxetera
Komórki	t{6,3}
Twarze	trójkąt {3} dwunastokąt {12}
figura wierzchołka	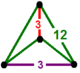tetragonalny disfenoid
zespół Coxetera	${\ Displaystyle 2 \ razy {\ overline {Y}} _ {3}}$ , [[3,6,3]]
Nieruchomości	Przechodnie wierzchołków, przechodnie krawędzi, przechodnie komórki

Bitruncated trójkątny kafelkowy plaster miodu , ma ścięte sześciokątne kafelkowe komórki, z tetragonalną figurą wierzchołka disfenoidalnego .

Kantelowany trójkątny plaster miodu z płytek

Kantelowany trójkątny plaster miodu z płytek
Typ	Parakompaktowy jednolity plaster miodu
Symbol Schläfliego	rr{3,6,3} lub t 0,2 {3,6,3} s 2 {3,6,3}
Diagram Coxetera
Komórki	rr{6,3} r{6,3} {}×{3}
Twarze	trójkąt {3} kwadrat {4} sześciokąt {6}
figura wierzchołka	klin
zespół Coxetera	${\ Displaystyle {\ overline {Y}} _ {3}}$ , [3,6,3]
Nieruchomości	Przechodnie wierzchołków

Kantelowany trójkątny plaster miodu z kafelkami , ma rombittriheksagonalne kafelki , triheksagonalne kafelki i trójkątne pryzmaty z figurą wierzchołka klina .

Symetria

Może być również zbudowana jako kantyk zadarty trójkątny dachówka o strukturze plastra miodu , , forma półsymetryczna z symetrią [3 ⁺ ,6,3].

Ukośnie ścięty trójkątny plaster miodu

Ukośnie ścięty trójkątny plaster miodu
Typ	Parakompaktowy jednolity plaster miodu
Symbol Schläfliego	tr{3,6,3} lub t 0,1,2 {3,6,3}
Diagram Coxetera
Komórki	tr{6,3} t{6,3} {}×{3}
Twarze	trójkąt {3} kwadrat {4} sześciokąt {6} dwunastokąt {12}
figura wierzchołka	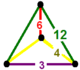lustrzany sferoidalny
zespół Coxetera	${\ Displaystyle {\ overline {Y}} _ {3}}$ , [3,6,3]
Nieruchomości	Przechodnie wierzchołków

Skośnie ścięty trójkątny plaster miodu ma ściętą trójheksagonalną płytkę , ściętą sześciokątną płytkę i trójkątne pryzmaty z lustrzanym kształtem wierzchołka sferycznego.

Ułożony trójkątny plaster miodu z płytek

Ułożony trójkątny plaster miodu z płytek
Typ	Parakompaktowy jednolity plaster miodu
Symbol Schläfliego	t 0,3 {3,6,3}
Diagram Coxetera
Komórki	{3,6} {}×{3}
Twarze	trójkąt {3} kwadrat {4}
figura wierzchołka	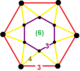sześciokątny antygraniastosłup
zespół Coxetera	${\ Displaystyle 2 \ razy {\ overline {Y}} _ {3}}$ , [[3,6,3]]
Nieruchomości	Przechodnie wierzchołków, przechodnie krawędzi

Przebiegnięty trójkątny plaster miodu z płytkami ma trójkątne płytki i trójkątne pryzmaty z sześciokątną figurą wierzchołka antygraniastosłupa .

Okrągły trójkątny plaster miodu

Okrągły trójkątny plaster miodu
Typ	Parakompaktowy jednolity plaster miodu
symbole Schläfliego	t 0,1,3 {3,6,3} s 2,3 {3,6,3}
Diagramy Coxetera
Komórki	t{3,6} rr{3,6} {}×{3} {}×{6}
Twarze	trójkąt {3} kwadrat {4} sześciokąt {6}
figura wierzchołka	ostrosłup równoramienny-trapezoidalny
zespół Coxetera	${\ Displaystyle {\ overline {Y}} _ {3}}$ , [3,6,3]
Nieruchomości	Przechodnie wierzchołków

Trójkątny plaster miodu ze ściętym trójkątem , , ma sześciokątne płytki , rombotwórcze sześciokątne płytki , trójkątny pryzmat i sześciokątne pryzmaty z figurą wierzchołka piramidy równoramiennej-trapezowej .

Symetria

Może być również zbudowany jako runcicantic zadarty trójkątny dachówka o strukturze plastra miodu , , forma półsymetryczna z symetrią [3 ⁺ ,6,3].

Omnitruncated trójkątny plaster miodu

Omnitruncated trójkątny plaster miodu
Typ	Parakompaktowy jednolity plaster miodu
Symbol Schläfliego	t 0,1,2,3 {3,6,3}
Diagram Coxetera
Komórki	tr{3,6} {}×{6}
Twarze	kwadrat {4} sześciokąt {6} dwunastokąt {12}
figura wierzchołka	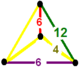phyllic disfenoid
zespół Coxetera	${\ Displaystyle 2 \ razy {\ overline {Y}} _ {3}}$ , [[3,6,3]]
Nieruchomości	Przechodnie wierzchołków, przechodnie krawędzi

Wielościenny trójkątny plaster miodu z kafelkami , ma ściętą trójheksagonalną płytkę i sześciokątne komórki graniastosłupa, z fylliczną figurą wierzchołka disfenoidalnego.

Trójkątny plaster miodu Runcisnub

Trójkątny plaster miodu Runcisnub
Typ	Parakompaktowy łuskowaty plaster miodu
Symbol Schläfliego	s 3 {3,6,3}
Diagram Coxetera
Komórki	r{6,3} {}x{3} {3,6} trik
Twarze	trójkąt {3} kwadrat {4} sześciokąt {6}
figura wierzchołka
zespół Coxetera	${\ Displaystyle {\ overline {Y}} _ {3}}$ , [3 + , 6,3]
Nieruchomości	Wierzchołek przechodni, niejednolity

Trójkątny plaster miodu runcisnub ma trójkątne płytki , trójkątne płytki , trójkątny pryzmat i trójkątne komórki kopuły. Jest przechodni przez wierzchołki , ale nie jednorodny, ponieważ zawiera solidne trójkątne komórki kopuły Johnsona.

Zobacz też

• Wypukłe jednolite plastry miodu w przestrzeni hiperbolicznej
• Regularne teselacje hiperbolicznej 3-przestrzeni
• Parakompaktowe jednolite plastry miodu

•   Coxeter , Regularne Polytopes , 3. red., Dover Publications, 1973. ISBN 0-486-61480-8 . (Tabele I i II: Regularne polytopy i plastry miodu, s. 294–296)
•     Piękno geometrii: dwanaście esejów (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (rozdział 10, regularne plastry miodu w przestrzeni hiperbolicznej ) Tabela III
•   Jeffrey R. Weeks The Shape of Space , wydanie 2 ISBN 0-8247-0709-5 (Rozdział 16-17: Geometrie na trzech rozmaitościach I, II)
• Norman Johnson Uniform Polytopes , rękopis
  • NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Rozprawa, University of Toronto, 1966
  • NW Johnson: Geometries and Transformations , (2018) Rozdział 13: Hiperboliczne grupy Coxetera