Zamów 4 sześciokątne płytki o strukturze plastra miodu
| Zamówienie-4 sześciokątne kafelki o strukturze plastra miodu | |
|---|---|
 Perspektywiczny widok projekcji w modelu dysku Poincarégo |
|
| Typ |
Hiperboliczny zwykły plaster miodu Parakompaktowy jednolity plaster miodu |
| Symbole Schläfliego |
{6,3,4} {6,3 1,1 } t 0,1 {(3,6) 2 } |
| Diagramy Coxetera |
 ↔ ↔ ↔ ↔ ↔ ↔ |
| Komórki |
{6,3} |
| Twarze | sześciokąt {6} |
| Rysunek krawędzi | kwadrat {4} |
| figura wierzchołka |
 oktaedr |
| Podwójny | Zamówienie-6 sześciennych plastra miodu |
| grupy Coxetera |
, [4,3,6] , [6, 3 1,1 ] , [(6,3) [2] ] |
| Nieruchomości | Regularne, quasiregularne |
W dziedzinie geometrii hiperbolicznej sześciokątny plaster miodu rzędu 4 powstaje jako jeden z 11 regularnych parakompaktowych plastrów miodu w trójwymiarowej przestrzeni hiperbolicznej . Jest parakompaktowy , ponieważ ma komórki złożone z nieskończonej liczby twarzy. Każda komórka jest sześciokątnym kafelkiem , którego wierzchołki leżą na horosferze : płaskiej płaszczyźnie w przestrzeni hiperbolicznej, która zbliża się do jednego idealnego punktu w nieskończoności.
Geometryczny plaster miodu to wypełnienie przestrzeni komórkami wielościennymi lub wielowymiarowymi , dzięki czemu nie ma luk. Jest to przykład bardziej ogólnego kafelkowania matematycznego lub teselacji w dowolnej liczbie wymiarów.
Plastry miodu są zwykle budowane w zwykłej przestrzeni euklidesowej („płaskiej”), podobnie jak wypukłe jednolite plastry miodu . Mogą być również konstruowane w przestrzeniach nieeuklidesowych , takich jak hiperboliczne jednolite plastry miodu . Dowolny skończony jednorodny polytope można rzutować na jego obwód , aby utworzyć jednolity plaster miodu w przestrzeni sferycznej.
Symbol Schläfli sześciokątnego plastra miodu w kolejności 4 to {6,3,4}. Ponieważ sześciokątne płytki to {6,3}, ten plaster miodu ma cztery takie sześciokątne płytki stykające się na każdej krawędzi. Ponieważ symbolem Schläfliego ośmiościanu jest {3,4}, wierzchołek tego plastra miodu jest ośmiościanem. Zatem osiem sześciokątnych nachyleń spotyka się w każdym wierzchołku tego plastra miodu, a sześć krawędzi spotykających się w każdym wierzchołku leży wzdłuż trzech ortogonalnych osi.
Obrazy
 Projekcja perspektywiczna |
 Jedna komórka widziana spoza sfery Poincarego |
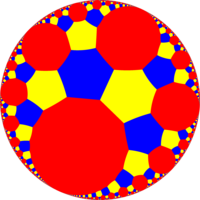 |
 Plaster miodu jest analogiczny do ułożenia apeirogonalnego rzędu H 2-4 , {∞,4}, pokazanego tutaj z jednym zielonym apeirogonem zarysowanym przez jego horocykl |
Symetria
Sześciokątny plaster miodu o strukturze plastra miodu rzędu 4 ma trzy odblaskowe konstrukcje o symetrii simplex.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Jednolita konstrukcja półsymetryczna {6,3 1,1 } ma dwa rodzaje (kolory) płytek heksagonalnych, z diagramem Coxetera ↔ . Istnieje również konstrukcja ćwierćsymetryczna, z czterema kolorami sześciokątnych płytek: .
Jednolita konstrukcja półsymetryczna {6,3 1,1 } ma dwa rodzaje (kolory) płytek heksagonalnych, z diagramem Coxetera ↔ . Istnieje również konstrukcja ćwierćsymetryczna, z czterema kolorami sześciokątnych płytek: .
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 Istnieją dodatkowe dwie odblaskowe symetrie z nieprostszymi domenami podstawowymi: [6,3 * ,4], który ma indeks 6, z diagramem Coxetera ; i [6, (3,4) * ], który ma indeks 48. Ten ostatni ma podstawową domenę sześcienną i ośmiościenny diagram Coxetera z trzema osiowymi nieskończonymi gałęziami: . Można to postrzegać jako użycie ośmiu kolorów do pokolorowania sześciokątnych płytek plastra miodu.
Istnieją dodatkowe dwie odblaskowe symetrie z nieprostszymi domenami podstawowymi: [6,3 * ,4], który ma indeks 6, z diagramem Coxetera ; i [6, (3,4) * ], który ma indeks 48. Ten ostatni ma podstawową domenę sześcienną i ośmiościenny diagram Coxetera z trzema osiowymi nieskończonymi gałęziami: . Można to postrzegać jako użycie ośmiu kolorów do pokolorowania sześciokątnych płytek plastra miodu.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Sześciokątny plaster miodu rzędu 4 zawiera , które układają 2- hipercykliczne powierzchnie i są podobne do ściętego trójkątnego układania nieskończonego rzędu , :
Sześciokątny plaster miodu rzędu 4 zawiera , które układają 2- hipercykliczne powierzchnie i są podobne do ściętego trójkątnego układania nieskończonego rzędu , :
Powiązane polytopy i plastry miodu
Sześciokątny plaster miodu rzędu 4 to regularny hiperboliczny plaster miodu w przestrzeni 3 i jeden z 11, które są parakompaktowe.
| 11 parakompaktowych zwykłych plastrów miodu | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 {6,3,3} |
 {6,3,4} |
 {6,3,5} |
 {6,3,6} |
 {4,4,3} |
 {4,4,4} |
||||||
 {3,3,6} |
 {4,3,6} |
 {5,3,6} |
 {3,6,3} |
 {3,4,4} |
|||||||
Istnieje piętnaście jednolitych plastrów miodu w rodzinie grupy [6,3,4] Coxeter , w tym ta regularna forma i jej podwójny , sześcienny plaster miodu rzędu 6 .
| [6,3,4] rodzinne plastry miodu | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| {6,3,4} | r{6,3,4} | t{6,3,4} | rrr{6,3,4} | t 0,3 {6,3,4} | tr{6,3,4} | t 0,1,3 {6,3,4} | t 0,1,2,3 {6,3,4} | ||||

|

|

|

|

|

|

|

|
||||

|

|

|

|

|

|

|
|||||
| {4,3,6} | r{4,3,6} | t{4,3,6} | rrr{4,3,6} | 2t{4,3,6} | tr{4,3,6} | t 0,1,3 {4,3,6} | t 0,1,2,3 {4,3,6} | ||||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Sześciokątny plaster miodu rzędu 4 ma powiązany naprzemienny plaster miodu, ↔ , z trójkątnymi płytkami i ośmiościanami .
Sześciokątny plaster miodu rzędu 4 ma powiązany naprzemienny plaster miodu, ↔ , z trójkątnymi płytkami i ośmiościanami .
Jest to część ciągu regularnych plastrów miodu o postaci {6,3,p}, z których wszystkie składają się z heksagonalnych komórek płytek:
| {6,3,p} plastry miodu | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Przestrzeń | H 3 | ||||||||||
| Formularz | Parakompaktowy | Niekompaktowy | |||||||||
| Nazwa | {6,3,3} | {6,3,4} | {6,3,5} | {6,3,6} | {6,3,7} | {6,3,8} | ... {6,3,∞} | ||||
| Obraz |

|

|

|

|

|

|

|
||||
| Coxetera |
|
|
|
|
|
|
|
||||
|
Figura wierzchołka {3,p} |
{3,3} |
{3,4} |
{3,5} |
{3,6} |
{3,7} |
{3,8} |
{3,∞} |
||||
Ten plaster miodu jest również spokrewniony z 16-komorowym , sześciennym plastrem miodu i dwunastościennym plastrem miodu rzędu 4 , z których wszystkie mają ośmiościenne figury wierzchołków.
| {p,3,4} zwykłe plastry miodu | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Przestrzeń | S 3 | E 3 | H 3 | ||||||||
| Formularz | Skończone | afiniczny | Kompaktowy | Parakompaktowy | Niekompaktowy | ||||||
| Nazwa |
{3,3,4} |
{4,3,4} |
{5,3,4} |
{6,3,4} |
{7,3,4} |
{8,3,4} |
... {∞,3,4} |
||||
| Obraz |

|

|

|

|

|

|

|
||||
| Komórki |
{3,3} |
{4,3} |
{5,3} |
{6,3} |
{7,3} |
{8,3} |
{∞,3} |
||||
Wspomniane plastry miodu są również quasiregularne:
| Regularne i quasiregularne plastry miodu: {p,3,4} i {p,3 1,1 } | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Przestrzeń | Euklidesowa 4-przestrzeń | Euklidesowa 3-przestrzeń | Hiperboliczna 3-przestrzeń | ||||||||
| Nazwa |
{3,3,4} {3,3 1,1 } = |
{4,3,4} {4,3 1,1 } = |
{5,3,4} {5,3 1,1 } = |
{6,3,4} {6,3 1,1 } = |
|||||||
|
Diagram Coxetera |
|
|
|
|
|||||||
|
Komórki {p,3} |
 |
 |
 |
 |
|||||||
| obrazu |

|

|

|

|
|||||||
Rektyfikowany porządek - 4 sześciokątne płytki o strukturze plastra miodu
| Rektyfikowany porządek - 4 sześciokątne płytki o strukturze plastra miodu | |
|---|---|
| Typ | Parakompaktowy jednolity plaster miodu |
| symbole Schläfliego | r{6,3,4} lub t 1 {6,3,4} |
| Diagramy Coxetera |
|
| Komórki |
{3,4} r{6,3} |
| Twarze |
trójkąt {3} sześciokąt {6} |
| figura wierzchołka |
 pryzmat kwadratowy |
| grupy Coxetera |
, [4,3,6] , [4, 3 [3] ] [6,3 1,1 ] , [3 []×[] ] |
| Nieruchomości | Przechodnie wierzchołków, przechodnie krawędzi |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Sześciokątny plaster miodu z rektyfikowanego rzędu 4 , t 1 {6,3,4}, ma ośmiościenne i triheksagonalne fasetki z płytkami, z kwadratową figurą wierzchołka pryzmatu .
Sześciokątny plaster miodu z rektyfikowanego rzędu 4 , t 1 {6,3,4}, ma ośmiościenne i triheksagonalne fasetki z płytkami, z kwadratową figurą wierzchołka pryzmatu .
![]()
![]()
![]()
![]()
![]() Jest podobny do hiperbolicznego tetraapeirogonalnego kafelkowania 2D , r {∞,4}, które naprzemiennie apeirogonalne i kwadratowe ściany:
Jest podobny do hiperbolicznego tetraapeirogonalnego kafelkowania 2D , r {∞,4}, które naprzemiennie apeirogonalne i kwadratowe ściany:
Ścięty porządek - 4 sześciokątne płytki o strukturze plastra miodu
| Ścięty porządek - 4 sześciokątne płytki o strukturze plastra miodu | |
|---|---|
| Typ | Parakompaktowy jednolity plaster miodu |
| Symbol Schläfliego | t{6,3,4} lub t 0,1 {6,3,4} |
| Diagram Coxetera |
|
| Komórki |
{3,4} t{6,3} |
| Twarze |
trójkąt {3} dwunastokąt {12} |
| figura wierzchołka |
 kwadratowa Piramida |
| grupy Coxetera |
, [4,3,6] , [6, 3 1,1 ] |
| Nieruchomości | Przechodnie wierzchołków |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Ścięty sześciokątny plaster miodu rzędu 4 , t 0,1 {6,3,4}, ma ośmiościan i ścięte sześciokątne płytki, z kwadratową figurą wierzchołka piramidy .
Ścięty sześciokątny plaster miodu rzędu 4 , t 0,1 {6,3,4}, ma ośmiościan i ścięte sześciokątne płytki, z kwadratową figurą wierzchołka piramidy .
![]()
![]()
![]()
![]()
![]() Jest podobny do dwuwymiarowego, hiperbolicznego , obciętego rzędu 4 apeirogonalnego kafelkowania , t {∞,4}, z apeirogonalnymi i kwadratowymi ścianami:
Jest podobny do dwuwymiarowego, hiperbolicznego , obciętego rzędu 4 apeirogonalnego kafelkowania , t {∞,4}, z apeirogonalnymi i kwadratowymi ścianami:
Bitruncated order-4 sześciokątne płytki o strukturze plastra miodu
| Bitruncated order-4 sześciokątne płytki o strukturze plastra miodu | |
|---|---|
| Typ | Parakompaktowy jednolity plaster miodu |
| Symbol Schläfliego | 2t{6,3,4} lub t 1,2 {6,3,4} |
| Diagram Coxetera |
|
| Komórki |
t{4,3} t{3,6} |
| Twarze |
kwadrat {4} sześciokąt {6} |
| figura wierzchołka |
 digonalny disfenoid |
| grupy Coxetera |
, [4,3,6] , [4, 3 [3] ] [6,3 1,1 ] , [3 []×[] ] |
| Nieruchomości | Przechodnie wierzchołków |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Sześciokątny plaster miodu z bitruncated rzędu 4 , t 1,2 {6,3,4}, ma ścięte ośmiościan i sześciokątne komórki układające, z dwukątną figurą wierzchołka disfenoidalnego .
Sześciokątny plaster miodu z bitruncated rzędu 4 , t 1,2 {6,3,4}, ma ścięte ośmiościan i sześciokątne komórki układające, z dwukątną figurą wierzchołka disfenoidalnego .
Kantelowany porządek - 4 sześciokątne płytki o strukturze plastra miodu
| Kantelowany porządek - 4 sześciokątne płytki o strukturze plastra miodu | |
|---|---|
| Typ | Parakompaktowy jednolity plaster miodu |
| Symbol Schläfliego | rr{6,3,4} lub t 0,2 {6,3,4} |
| Diagram Coxetera |
|
| Komórki |
r{3,4} {}x{4} r{6,3} |
| Twarze |
trójkąt {3} kwadrat {4} sześciokąt {6} |
| figura wierzchołka |
 klin |
| grupy Coxetera |
, [4,3,6] , [6, 3 1,1 ] |
| Nieruchomości | Przechodnie wierzchołków |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Kantelowany sześciokątny plaster miodu o strukturze plastra miodu rzędu 4 , t 0,2 {6,3,4}, ma sześcienny ośmiościan , sześcian i rombitrisześciokątne komórki układające płytki z figurą wierzchołka klina .
Kantelowany sześciokątny plaster miodu o strukturze plastra miodu rzędu 4 , t 0,2 {6,3,4}, ma sześcienny ośmiościan , sześcian i rombitrisześciokątne komórki układające płytki z figurą wierzchołka klina .
Cantitruncated order - 4 sześciokątne płytki o strukturze plastra miodu
| Cantitruncated order - 4 sześciokątne płytki o strukturze plastra miodu | |
|---|---|
| Typ | Parakompaktowy jednolity plaster miodu |
| Symbol Schläfliego | tr{6,3,4} lub t 0,1,2 {6,3,4} |
| Diagram Coxetera |
|
| Komórki |
t{3,4} {}x{4} tr{6,3} |
| Twarze |
kwadrat {4} sześciokąt {6} dwunastokąt {12} |
| figura wierzchołka |
 lustrzany sferoidalny |
| grupy Coxetera |
, [4,3,6] , [6, 3 1,1 ] |
| Nieruchomości | Przechodnie wierzchołków |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Ukośnie ścięty sześciokątny plaster miodu rzędu 4 , t 0,1,2 {6,3,4}, ma ścięty ośmiościan , sześcian i obcięte trójheksagonalne komórki kafelkowe, z lustrzaną figurą sferoidalnego wierzchołka .
Ukośnie ścięty sześciokątny plaster miodu rzędu 4 , t 0,1,2 {6,3,4}, ma ścięty ośmiościan , sześcian i obcięte trójheksagonalne komórki kafelkowe, z lustrzaną figurą sferoidalnego wierzchołka .
Runcinated order-4 sześciokątne kafelki o strukturze plastra miodu
| Runcinated order-4 sześciokątne kafelki o strukturze plastra miodu | |
|---|---|
| Typ | Parakompaktowy jednolity plaster miodu |
| Symbol Schläfliego | t 0,3 {6,3,4} |
| Diagram Coxetera |
|
| Komórki |
{4,3} {}x{4} {6,3} {}x{6} |
| Twarze |
kwadrat {4} sześciokąt {6} |
| figura wierzchołka |
 nieregularny trójkątny antygraniastosłup |
| grupy Coxetera | , [4,3,6] |
| Nieruchomości | Przechodnie wierzchołków |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Sześciokątny plaster miodu o kształcie runcinated rzędu 4 , t 0,3 {6,3,4}, ma sześcian , sześciokątne kafelki i sześciokątne pryzmaty , z nieregularną trójkątną figurą wierzchołka antygraniastosłupa .
Sześciokątny plaster miodu o kształcie runcinated rzędu 4 , t 0,3 {6,3,4}, ma sześcian , sześciokątne kafelki i sześciokątne pryzmaty , z nieregularną trójkątną figurą wierzchołka antygraniastosłupa .
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Zawiera dwuwymiarowe hiperboliczne kafelki rombittraheksagonalne rr{4,6}, z kwadratowymi i sześciokątnymi powierzchniami. Płytka ma również konstrukcję półsymetryczną .
Zawiera dwuwymiarowe hiperboliczne kafelki rombittraheksagonalne rr{4,6}, z kwadratowymi i sześciokątnymi powierzchniami. Płytka ma również konstrukcję półsymetryczną .

|
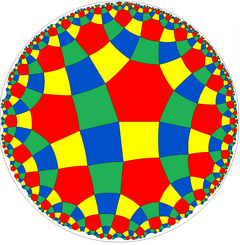
|
|
|
|
|---|
Runcitruncated order-4 sześciokątne płytki o strukturze plastra miodu
| Runcitruncated order-4 sześciokątne płytki o strukturze plastra miodu | |
|---|---|
| Typ | Parakompaktowy jednolity plaster miodu |
| Symbol Schläfliego | t 0,1,3 {6,3,4} |
| Diagram Coxetera |
|
| Komórki |
rr{3,4} {}x{4} {}x{12} t{6,3} |
| Twarze |
trójkąt {3} kwadrat {4} dwunastokąt {12} |
| figura wierzchołka |
ostrosłup równoramienny-trapezoidalny |
| grupy Coxetera | , [4,3,6] |
| Nieruchomości | Przechodnie wierzchołków |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Sześciokątny plaster miodu o strukturze plastra miodu w kształcie ściętego rzędu 4 , t 0,1,3 {6,3,4}, ma ośmiościan rombowy , sześcian , graniastosłup dwunastokątny i ścięte sześciokątne komórki układające się w kafelki, z figurą wierzchołka piramidy równoramiennej-trapezoidalnej .
Sześciokątny plaster miodu o strukturze plastra miodu w kształcie ściętego rzędu 4 , t 0,1,3 {6,3,4}, ma ośmiościan rombowy , sześcian , graniastosłup dwunastokątny i ścięte sześciokątne komórki układające się w kafelki, z figurą wierzchołka piramidy równoramiennej-trapezoidalnej .
Runcicantellated order-4 sześciokątne kafelki o strukturze plastra miodu
Sześciokątny plaster miodu z runcicantelated rzędu-4 jest taki sam jak sześcienny plaster miodu rzędu runcitruncated-6 .
Omnitruncated order-4 sześciokątne płytki o strukturze plastra miodu
| Omnitruncated order-4 sześciokątne płytki o strukturze plastra miodu | |
|---|---|
| Typ | Parakompaktowy jednolity plaster miodu |
| Symbol Schläfliego | t 0,1,2,3 {6,3,4} |
| Diagram Coxetera |
|
| Komórki |
tr{4,3} tr{6,3} {}x{12} {}x{8} |
| Twarze |
kwadrat {4} sześciokąt {6} ośmiokąt {8} dwunastokąt {12} |
| figura wierzchołka |
 nieregularny czworościan |
| grupy Coxetera | , [4,3,6] |
| Nieruchomości | Przechodnie wierzchołków |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Sześciokątny plaster miodu o kształcie omnitruncated rzędu 4 , t 0,1,2,3 {6,3,4}, ma ścięty ośmiościan sześcienny , ściętą trójheksagonalną płytkę , dwunastokątny pryzmat i ośmiokątne komórki graniastosłupa , z nieregularną figurą wierzchołka czworościanu .
Sześciokątny plaster miodu o kształcie omnitruncated rzędu 4 , t 0,1,2,3 {6,3,4}, ma ścięty ośmiościan sześcienny , ściętą trójheksagonalną płytkę , dwunastokątny pryzmat i ośmiokątne komórki graniastosłupa , z nieregularną figurą wierzchołka czworościanu .
Alternatywna kolejność - 4 sześciokątne płytki o strukturze plastra miodu
| Alternatywna kolejność - 4 sześciokątne płytki o strukturze plastra miodu | |
|---|---|
| Typ |
Parakompaktowy jednolity plaster miodu Półregularny plaster miodu |
| symbole Schläfliego | h{6,3,4} |
| Diagramy Coxetera |
|
| Komórki |
{3 [3] } {3,4} |
| Twarze | trójkąt {3} |
| figura wierzchołka |
ścięty ośmiościan |
| grupy Coxetera | , [4,3 [3] ] |
| Nieruchomości | Przechodnie wierzchołków, przechodnie krawędzi, quasiregularne |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Sześciokątny plaster miodu o naprzemiennym porządku - 4 , ↔ , składa się z trójkątnych płytek i komórek ośmiościanu , w postaci ściętego wierzchołka ośmiościanu .
Sześciokątny plaster miodu o naprzemiennym porządku - 4 , ↔ , składa się z trójkątnych płytek i komórek ośmiościanu , w postaci ściętego wierzchołka ośmiościanu .
Zamówienie kantyckie - 4 sześciokątne płytki o strukturze plastra miodu
| Zamówienie kantyckie - 4 sześciokątne płytki o strukturze plastra miodu | |
|---|---|
| Typ | Parakompaktowy jednolity plaster miodu |
| symbole Schläfliego | godz. 2 {6,3,4} |
| Diagramy Coxetera |
|
| Komórki |
h 2 {6,3} t{3,4} r{3,4} |
| Twarze |
trójkąt {3} kwadrat {4} sześciokąt {6} |
| figura wierzchołka |
 klin |
| grupy Coxetera | , [4,3 [3] ] |
| Nieruchomości | Przechodnie wierzchołków |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Kantyczny porządek - 4 sześciokątny kafelkowy plaster miodu , ↔ , składa się z trójheksagonalnego kafelkowego , ściętego ośmiościanu i sześciennych komórek ośmiościanu z figurą wierzchołka klina .
Kantyczny porządek - 4 sześciokątny kafelkowy plaster miodu , ↔ , składa się z trójheksagonalnego kafelkowego , ściętego ośmiościanu i sześciennych komórek ośmiościanu z figurą wierzchołka klina .
Runcic order-4 sześciokątne kafelki o strukturze plastra miodu
| Runcic order-4 sześciokątne kafelki o strukturze plastra miodu | |
|---|---|
| Typ | Parakompaktowy jednolity plaster miodu |
| symbole Schläfliego | h 3 {6,3,4} |
| Diagramy Coxetera |
|
| Komórki |
{3 [3] } rr{3,4} {4,3} {}x{3} |
| Twarze |
trójkąt {3} kwadrat {4} |
| figura wierzchołka |
 trójkątna kopuła |
| grupy Coxetera | , [4,3 [3] ] |
| Nieruchomości | Przechodnie wierzchołków |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Sześciokątny plaster miodu runcic rzędu - 4 , ↔ , składa się z trójkątnych płytek , ośmiościanu rombowego , sześcianu i trójkątnych pryzmatów z trójkątną figurą wierzchołka kopuły .
Sześciokątny plaster miodu runcic rzędu - 4 , ↔ , składa się z trójkątnych płytek , ośmiościanu rombowego , sześcianu i trójkątnych pryzmatów z trójkątną figurą wierzchołka kopuły .
Kolejność Runcicantic - 4 sześciokątne płytki o strukturze plastra miodu
| Kolejność Runcicantic - 4 sześciokątne płytki o strukturze plastra miodu | |
|---|---|
| Typ | Parakompaktowy jednolity plaster miodu |
| symbole Schläfliego | h 2,3 {6,3,4} |
| Diagramy Coxetera |
|
| Komórki |
h 2 {6,3} tr{3,4} t{4,3} {}x{3} |
| Twarze |
trójkąt {3} kwadrat {4} sześciokąt {6} ośmiokąt {8} |
| figura wierzchołka |
 ostrosłup prostokątny |
| grupy Coxetera | , [4,3 [3] ] |
| Nieruchomości | Przechodnie wierzchołków |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() runcicantic rzędu 4 , ↔ , składa się z triheksagonalnych płytek , ściętego sześciennego ośmiościanu , ściętego sześcianu i trójkątnych komórek graniastosłupa , z prostokątną figurą wierzchołka piramidy .
runcicantic rzędu 4 , ↔ , składa się z triheksagonalnych płytek , ściętego sześciennego ośmiościanu , ściętego sześcianu i trójkątnych komórek graniastosłupa , z prostokątną figurą wierzchołka piramidy .
Zamówienie ćwiartki - 4 sześciokątne płytki o strukturze plastra miodu
| Zamówienie ćwiartki - 4 sześciokątne płytki o strukturze plastra miodu | |
|---|---|
| Typ | Parakompaktowy jednolity plaster miodu |
| Symbol Schläfliego | q{6,3,4} |
| Diagram Coxetera |
|
| Komórki |
{3 [3] } {3,3} t{3,3} godz. 2 {6,3} |
| Twarze |
trójkąt {3} sześciokąt {6} |
| figura wierzchołka |
 trójkątna kopuła |
| grupy Coxetera | , [3 [] x [] ] |
| Nieruchomości | Przechodnie wierzchołków |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Sześciokątny plaster miodu o strukturze plastra miodu ćwiartki rzędu 4 , q{6,3,4} lub , składa się z trójkątnych płytek , triheksagonalnych płytek , czworościanu i ściętych komórek czworościanu z trójkątną figurą wierzchołka kopuły .
Sześciokątny plaster miodu o strukturze plastra miodu ćwiartki rzędu 4 , q{6,3,4} lub , składa się z trójkątnych płytek , triheksagonalnych płytek , czworościanu i ściętych komórek czworościanu z trójkątną figurą wierzchołka kopuły .
Zobacz też
- Wypukłe jednolite plastry miodu w przestrzeni hiperbolicznej
- Regularne teselacje hiperbolicznej 3-przestrzeni
- Parakompaktowe jednolite plastry miodu
- Coxeter , Regularne Polytopes , 3. red., Dover Publications, 1973. ISBN 0-486-61480-8 . (Tabele I i II: Regularne polytopy i plastry miodu, s. 294–296)
- Piękno geometrii: dwanaście esejów (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (rozdział 10, regularne plastry miodu w przestrzeni hiperbolicznej ) Tabela III
- Jeffrey R. Weeks The Shape of Space , wydanie 2 ISBN 0-8247-0709-5 (Rozdział 16-17: Geometrie na trzech rozmaitościach I, II)
-
Norman Johnson Uniform Polytopes , rękopis
- NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Rozprawa, University of Toronto, 1966
- NW Johnson: Geometries and Transformations , (2018) Rozdział 13: Hiperboliczne grupy Coxetera




















