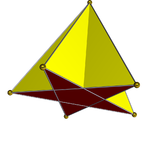
Piramida pięciokątna

Piramida pięciokątna
Typ	Johnson J 1 – J 2 – J 3
Twarze	5 trójkątów 1 pięciokąt
Krawędzie	10
Wierzchołki	6
Konfiguracja wierzchołków	5(3 2,5 ) (3 5 )
Symbol Schläfliego	( ) ∨ {5}
Grupa symetrii	C 5v , [5], (*55)
Grupa rotacyjna	do 5 , [5] + , (55)
Podwójny wielościan	samego siebie
Nieruchomości	wypukły
Internet

Model 3D pięciokątnej piramidy

W geometrii pięciokątna piramida to piramida z pięciokątną podstawą, na której wzniesiono pięć trójkątnych ścian, które spotykają się w punkcie ( wierzchołek ). Jak każda piramida , jest samodualna .

Regularna pięciokątna piramida ma podstawę, która jest regularnym pięciokątem i ściany boczne, które są trójkątami równobocznymi . Jest to jedna z brył Johnsona ( J ₂ ).

Można to postrzegać jako „pokrywę” dwudziestościanu ; reszta dwudziestościanu tworzy J ₁₁ wydłużoną pięciokątną piramidę .

Mówiąc bardziej ogólnie, piramidę pięciokątną o jednolitym rzędzie 2 wierzchołków można zdefiniować za pomocą regularnej pięciokątnej podstawy i 5 boków trójkąta równoramiennego o dowolnej wysokości.

współrzędne kartezjańskie

Pięciokątna piramida może być postrzegana jako „pokrywa” regularnego dwudziestościanu ; reszta dwudziestościanu tworzy wydłużoną pięciokątną piramidę J ₁₁ . Ze współrzędnych kartezjańskich dwudziestościanu współrzędne kartezjańskie pięciokątnej piramidy o długości krawędzi 2 można wywnioskować jako

$1),\,(\tau ,1,0),(\tau ,-1,0),(0,-\tau ,1)}$

gdzie 𝜏 (czasami zapisywane jako φ ) to złoty podział .

Wysokość H od środka pięciokątnej ściany do wierzchołka ostrosłupa pięciokątnego o długości krawędzi a można zatem obliczyć jako:

${\ Displaystyle H = \ lewo ({\ sqrt {\ Frac {5- {\ sqrt {5}}} {10}}} \ prawo) a \ około 0,52573a.}$

Jego pole powierzchni A można obliczyć jako pole podstawy pięciokąta plus pięciokrotność pola jednego trójkąta:

${\ Displaystyle A = {\ Frac {a ^ {2}}} {2}} {\ sqrt {{\ Frac {5} {2}} \ lewo (10 + {\ sqrt {5}} + {\ sqrt {75 + 30 {\ sqrt {5}}}} \ prawo)}} \ około 3,88554 \ cdot a ^ {2}.}$

Jego objętość można obliczyć ze wzoru:

${\ Displaystyle V = \ lewo ({\ Frac {5 + {\ sqrt {5}}} {24}} \ prawo) a ^ {3} \ około 0,30150a ^ {3}.}$

Powiązane wielościany

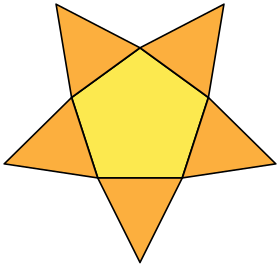
Pentagramowa piramida gwiazd ma ten sam układ wierzchołków , ale jest połączona z podstawą pentagramu :

Zwykłe piramidy
Digonalny	Trójkątny	Kwadrat	Pięciokątny	Sześciokątny	siedmiokątny	Ośmioboczny	Enneagonalny	Dziesięciokątny...
Niewłaściwy	Regularny	Równoboczny		Równoramienny

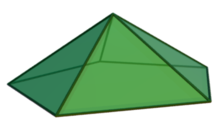
Pentagonal frustum to pięciokątna piramida ze ściętym wierzchołkiem

Szczyt dwudziestościanu to pięciokątna piramida

Przykład

Piramida pięciokątna (w Matemateca IME-USP )

Linki zewnętrzne

• Eric W. Weisstein , Pięciokątna piramida ( bryła Johnsona ) w MathWorld .
• Wirtualna rzeczywistość Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra ( model VRML )