Bilunabirotunda

Bilunabirotunda
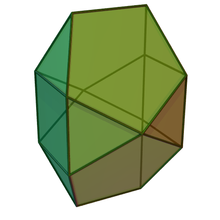Typ	Johnson J 90 – J 91 – J 92
Twarze	2x4 trójkąty 2 kwadraty 4 pięciokąty
Krawędzie	26
Wierzchołki	14
Konfiguracja wierzchołków	4(3.5 2 ) 8(3.4.3.5) 2(3.5.3.5)
Grupa symetrii	D 2 godz
Podwójny wielościan	-
Nieruchomości	wypukły
Internet

Model 3D bilunabirotundy

W geometrii bilunabirotunda jest jedną z brył Johnsona ( J ₎ 91 . Bryła Johnsona jest jednym z 92 ściśle wypukłych wielościanów , które składają się z regularnych ścian wielokątów, ale nie są jednolitymi wielościanami (to znaczy nie są bryłami platońskimi , bryłami Archimedesa , graniastosłupami ani antygraniastosłupami ). Zostały one nazwane przez Normana Johnsona , który jako pierwszy wymienił te wielościany w 1966 roku.

Geometria

Jest to jedna z elementarnych brył Johnsona, które nie powstają w wyniku manipulacji „wytnij i wklej” bryłami platońskimi i archimedesowymi .

Jednak ma silny związek z dwudziestościanem , bryłą Archimedesa. Jedno z dwóch skupisk dwóch pięciokątów i dwóch trójkątów można wyrównać z przystającą plamą twarzy na dwudziestościanie. Jeśli dwa bilunabirotundae są ustawione w ten sposób po przeciwnych stronach dwudziestościanu, to dwa wierzchołki bilunabirotundae spotykają się w samym środku dwudziestościanu.

Pozostałe dwa skupiska twarzy bilunabirotundy, lunes (każdy lune zawiera dwa trójkąty sąsiadujące z przeciwległymi bokami jednego kwadratu), można wyrównać z przystającą plamą twarzy na rombicosidodecahedron . Jeśli dwa bilunabirotundae są ustawione w ten sposób po przeciwnych stronach rombicosidodecahedru, to sześcian można umieścić między bilunabirotundami w samym środku rombicosidodecahedronu.

również wyrównać z pięciokątnymi ścianami dwudziestościanu metabidiminowanego .

Bilunabirotunda ma słaby związek z ośmiościanem sześciennym , ponieważ można go utworzyć, zastępując cztery kwadratowe ściany ośmiościanu ośmiościanem pięciokątami.

Pełny obrót bilunabirotundy, zdjęcie co 15°.

współrzędne kartezjańskie

Poniższe definiują wierzchołki bilunabirotundy wyśrodkowane w początku o długości krawędzi 1:

${\ Displaystyle \ lewo (0,0, \ pm {\ Frac {\ varphi} {2}} \ prawej)}$

${\ Displaystyle \ lewo (\pm {\frac {\varphi +1}{2}},\pm {\frac {1}{2}},0\prawo)}$

${ \ displaystyle \ lewo (\ pm {\ frac {1} {2}}, \ pm {\ frac {\ varphi} {2}}, \ pm {\ frac {1} {2}} \ prawej)}$

gdzie ${\ Displaystyle \ varphi = {\ Frac {1 + {\ sqrt {5}}} {2}}}$ to złoty podział .

Powiązane wielościany i plastry miodu

Dalsze informacje: Regular_dodecahedron § Space_filling_with_cube_and_bilunabirotunda

Sześć bilunabirotundae można powiększyć wokół sześcianu o symetrii pirytoedrycznej . BM Stewart oznaczył ten model z sześcioma bilunabirotundami jako 6J ₉₁ (P ₄ ).

Bilunabirotunda może być używana z regularnym dwunastościanem i kostką jako wypełniający przestrzeń plaster miodu.

Wypełniający przestrzeń plaster miodu

6 bilunabirotundae wokół sześcianu

Animacja teselacji sześcianów, dwunastościanów i bilunabirotundy 12 bilunabirotundae wokół dwunastościanu

Linki zewnętrzne

• Eric W. Weisstein , Bilunabirotunda ( solidny Johnson ) w MathWorld .
• Cudowne wypełnianie przestrzeni (Dwunastościan i sześcian i Johnson solid nr 91)