Kwadratowa ortobicupola
| Kwadratowa ortobicupola | |
|---|---|
 | |
| Typ |
Johnson J 27 – J 28 – J 29 |
| Twarze |
8 trójkątów 2+8 kwadratów |
| Krawędzie | 32 |
| Wierzchołki | 16 |
| Konfiguracja wierzchołków | 8(3 2 ,4 2 ) 8(3,4 3 ) |
| Grupa symetrii | D 4 godz |
| Podwójny wielościan | - |
| Nieruchomości | wypukły |
| Internet | |
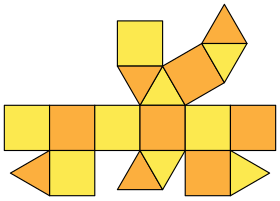 | |
W geometrii kwadratowa ortobicupola jest jedną z brył Johnsona ( J 28 ). Jak sama nazwa wskazuje, można ją zbudować, łącząc dwie kwadratowe kopuły ( J 4 ) wzdłuż ich ośmiokątnych podstaw, dopasowując do siebie podobne ściany. Obrót o 45 stopni jednej kopuły przed połączeniem daje kwadratową żyrobikupolę ( J 29 ).
Bryła Johnsona jest jednym z 92 ściśle wypukłych wielościanów , które składają się z regularnych ścian wielokątów, ale nie są jednolitymi wielościanami (to znaczy nie są bryłami platońskimi , bryłami Archimedesa , graniastosłupami ani antygraniastosłupami ). Zostały one nazwane przez Normana Johnsona , który jako pierwszy wymienił te wielościany w 1966 roku.
kopuła ortobicupola jest drugą w nieskończonym zbiorze kopuł .
Kwadratowa ortokopula może być wydłużona przez wstawienie ośmiokątnego graniastosłupa między jej dwie kopuły, aby uzyskać ośmiościan rombowy , lub zapadnięta przez usunięcie nieregularnego sześciokątnego pryzmatu, aby uzyskać wydłużoną kwadratową dypiramidę ( J 15 ), która sama w sobie jest jedynie wydłużonym ośmiościanem .
Można go zbudować z disphenocingulum ( J 90 ), zastępując pasmo trójkątów w górę iw dół pasmem prostokątów, jednocześnie mocując dwa przeciwległe sphenos .
Powiązane wielościany i plastry miodu
Kwadratowa ortobicupola tworzy wypełniające przestrzeń plastry miodu z czworościanami ; z kostkami i ośmiościanami sześciennymi ; z czworościanami i sześcianami; z ostrosłupami kwadratowymi , czworościanami i różnymi kombinacjami sześcianów, ostrosłupami wydłużonymi i/lub ostrosłupami kwadratowymi wydłużonymi .