Hebesfenorotunda trójkątna

Hebesfenorotunda trójkątna
Typ	Johnson J 91 – J 92 – J 1
Twarze	13 trójkątów 3 kwadraty 3 pięciokąty 1 sześciokąt
Krawędzie	36
Wierzchołki	18
Konfiguracja wierzchołków	3(3 3,5 ) 6(3.4.3,5) 3(3.5.3,5) 2,3(3 2,4,6 )
Grupa symetrii	C 3v
Podwójny wielościan	-
Nieruchomości	wypukły
Internet

Model 3D trójkątnej hebesfenorotundy

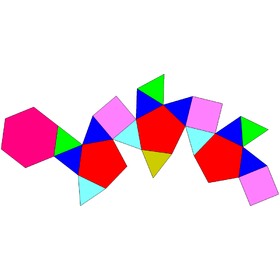W geometrii trójkątna hebesphenorotunda jest jedną z brył Johnsona ( J ₉₂ ).

Bryła Johnsona jest jednym z 92 ściśle wypukłych wielościanów , które składają się z regularnych ścian wielokątów, ale nie są jednolitymi wielościanami (to znaczy nie są bryłami platońskimi , bryłami Archimedesa , graniastosłupami ani antygraniastosłupami ). Zostały one nazwane przez Normana Johnsona , który jako pierwszy wymienił te wielościany w 1966 roku.

Jest to jedna z elementarnych brył Johnsona, które nie powstają w wyniku manipulacji „wytnij i wklej” bryłami platońskimi i archimedesowymi . Jednak ma silny związek z dwudziestościanem , bryłą Archimedesa. Najbardziej widoczna jest grupa trzech pięciokątów i czterech trójkątów po jednej stronie bryły. Jeśli te ściany są wyrównane z przystającą plamą ścian dwudziestościanu, wówczas sześciokątna ściana będzie leżeć w płaszczyźnie w połowie odległości między dwiema przeciwległymi trójkątnymi ścianami dwudziestościanu.

Trójkątna hebesfenorotunda ma również skupiska ścian, które można wyrównać z odpowiednimi ścianami rombicozydodekahedru : trzy księżyce , z których każdy składa się z kwadratu i dwóch antypodalnych trójkątów przylegających do kwadratu.

Ściany wokół każdego wierzchołka (3 ^{3 ,} 5) można również wyrównać z odpowiednimi ścianami różnych dwudziestościanów zmniejszonych .

Johnson używa przedrostka hebespheno- w odniesieniu do kompleksu przypominającego tępy klin, utworzonego przez trzy sąsiednie lune , przy czym lune jest kwadratem z trójkątami równobocznymi przymocowanymi po przeciwnych stronach. Przyrostek (trójkątny) -rotunda odnosi się do kompleksu trzech trójkątów równobocznych i trzech pięciokątów foremnych otaczających inny trójkąt równoboczny, który strukturalnie przypomina pięciokątną rotundę .

Trójkątna hebesfenorotunda jest jedyną bryłą Johnsona o ścianach z 3, 4, 5 i 6 boków.

współrzędne kartezjańskie

Współrzędne kartezjańskie dla trójkątnej hebesfenorotundy o długości krawędzi √ 5 – 1 są dane przez sumę orbit punktów

${\ Displaystyle \ lewo (0, - {\ Frac {2} {\ tau {\ sqrt {3}}} },{\frac {2\tau}{\sqrt {3}}}\right),\left(\tau,{\frac {1}{{\sqrt {3}}\tau ^{2}}} {\frac {2}{\sqrt {3}}}\right)}$

${\ Displaystyle \ lewo (\ tau, - {\ Frac {\ tau} {\ sqrt {3}}}, {\ Frac {2} {{\ sqrt {3}} \ tau}} \ prawej) ,\lewo({\frac {2}{\tau}},0,0\prawo),}$

pod działaniem grupy generowanej przez obrót o 120° wokół osi z i odbicie od płaszczyzny yz. Tutaj 𝜏 = √ 5 + 1 / 2 (czasami zapisywane jako φ ) to złoty podział . Pierwszy punkt generuje trójkąt naprzeciw sześciokąta, drugi punkt tworzy podstawy trójkątów otaczających poprzedni trójkąt, trzeci punkt generuje wierzchołki pięciokątów naprzeciw pierwszego trójkąta, a ostatni punkt generuje sześciokąt.

Można wtedy obliczyć pole powierzchni trójkątnej hebesfenorotundy o długości krawędzi a as

${\ Displaystyle A = \ lewo (3 + {\ Frac {1} {4}} {\ sqrt {1308 +90{\sqrt {5}}+114{\sqrt {75+30{\sqrt {5}}}}}}\right)a^{2}\około 16,38867a^{2},}$

a jego objętość jako

${\ Displaystyle V = {\ Frac {1} {6}} \ lewo (15 + 7 {\ sqrt {5}} \ prawo) a ^ {3} \ około 5,10875a ^ {3}.}$

Drugą, odwróconą, trójkątną hebesphenorotundę można uzyskać, negując drugą i trzecią współrzędną każdego punktu. Ten drugi wielościan zostanie połączony z pierwszym na ich wspólnej sześciokątnej powierzchni, a para wpisze dwudziestościan. Jeśli sześciokątna ściana zostanie przeskalowana według złotego podziału, wówczas wypukła otoczka wyniku będzie całym dwudziestościanem.

Linki zewnętrzne

• Eric W. Weisstein , Triangular hebesphenorotunda ( solid Johnson ) w MathWorld .