Sphenomegacorona

Sphenomegacorona
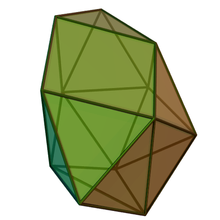Typ	Johnson J 87 – J 88 – J 89
Twarze	16 trójkątów 2 kwadraty
Krawędzie	28
Wierzchołki	12
Konfiguracja wierzchołków	2(3 4 ) 2 (3 2 ,4 2 ) 2x2 (3 5 ) 4(3 4,4 )
Grupa symetrii	C 2v
Podwójny wielościan	-
Nieruchomości	wypukły
Internet

Model 3D sphenomegacorona

W geometrii sphenomegacorona jest jedną z brył Johnsona ( J ₈₈ ) . Jest to jedna z elementarnych brył Johnsona, które nie powstają w wyniku manipulacji bryłami platońskimi i archimedesowymi metodą „wytnij i wklej” .

Bryła Johnsona jest jednym z 92 ściśle wypukłych wielościanów , które składają się z regularnych ścian wielokątów, ale nie są jednolitymi wielościanami (to znaczy nie są bryłami platońskimi , bryłami Archimedesa , graniastosłupami ani antygraniastosłupami ). Zostały one nazwane przez Normana Johnsona , który jako pierwszy wymienił te wielościany w 1966 roku.

Johnson używa przedrostka spheno- w odniesieniu do klinowatego kompleksu utworzonego przez dwie sąsiednie luny , przy czym lune jest kwadratem z trójkątami równobocznymi przymocowanymi po przeciwnych stronach. Podobnie przyrostek -megacorona odnosi się do przypominającego koronę kompleksu 12 trójkątów, w przeciwieństwie do mniejszego trójkątnego kompleksu, który tworzy sphenocorona . Połączenie obu kompleksów razem skutkuje sphenomegacorona.

współrzędne kartezjańskie

Niech k ≈ 0,59463 będzie najmniejszym dodatnim pierwiastkiem wielomianu

${\ Displaystyle {\ rozpocząć {wyrównane} i 1680x ^ {16} -4800x ^ {15} -3712x ^ {14} + 17216x ^ {13} + 1568x ^ {12}-24576x^{11}+2464x^{10}+17248x^{9}\\&\quad {}-3384x^{8}-5584x^{7}+2000x^{6}+240x^{ 5}-776x^{4}+304x^{3}+200x^{2}-56x-23.\end{wyrównane}}}$

Następnie współrzędne kartezjańskie sphenomegacorona o długości krawędzi 2 są dane przez sumę orbit punktów

${\ Displaystyle {\ rozpocząć {wyrównane} i \ lewo (0,1,2 {\ sqrt {1-k ^ {2}}} \ prawo), \, (2k, 1,0), \, \ lewo ( 0,{\frac {\sqrt {3-4k^{2}}}{\sqrt {1-k^{2}}}}+1,{\frac {1-2k^{2}}{\sqrt {1-k^{2}}}}\right),\\&\left(1,0,-{\sqrt {2+4k-4k^{2}}}\right),\,\left( 0,{\frac {{\sqrt {3-4k^{2}}}\left(2k^{2}-1\right)}{\left(k^{2}-1\right){\sqrt {1-k^{2}}}}}+1,{\frac {2k^{4}-1}{\left(1-k^{2}\right)^{\frac {3}{2 }}}}\prawo)\end{wyrównane}}}$

pod działaniem grupy generowanej przez refleksje o płaszczyźnie xz i płaszczyźnie yz.

Możemy wtedy obliczyć pole powierzchni sphenomegacorona o długości krawędzi a as

${\ Displaystyle A = \ lewo (2 + 4 {\ sqrt {3}} \ prawej) a ^ {2} \ około 8,92820a ^ {2}, }$

a jego objętość jako

${\ Displaystyle V = \ xi a ^ {3} \ około 1,94811a ^ {3},}$

gdzie rozwinięcie dziesiętne ξ jest podane przez A334114 .

Linki zewnętrzne

• Eric W. Weisstein , Sphenomegacorona ( solid Johnsona ) w MathWorld .