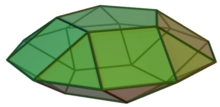
Żyrobiupola pięciokątna
| Żyrobiupola pięciokątna | |
|---|---|
 | |
| Typ |
Bicupola , Johnson J 30 – J 31 – J 32 |
| Twarze |
10 trójkątów 10 kwadratów 2 pięciokąty |
| Krawędzie | 40 |
| Wierzchołki | 20 |
| Konfiguracja wierzchołków | 10(3.4.3.4) 10(3.4.5.4) |
| Grupa symetrii | D 5d |
| Podwójny wielościan | Wydłużony pięciokątny trapez |
| Nieruchomości | wypukły |
| Internet | |
 | |
W geometrii pięciokątna gyrobicupola jest jedną z brył Johnsona ( J 31 ). Podobnie jak ortobicupola pięciokątna ( J 30 ), można ją uzyskać przez połączenie dwóch pięciobocznych kopuł ( J 5 ) wzdłuż ich podstaw. Różnica polega na tym, że w tej bryle dwie połówki są obrócone względem siebie o 36 stopni.
Bryła Johnsona jest jednym z 92 ściśle wypukłych wielościanów , które składają się z regularnych ścian wielokątów, ale nie są jednolitymi wielościanami (to znaczy nie są bryłami platońskimi , bryłami Archimedesa , graniastosłupami ani antygraniastosłupami ). Zostały one nazwane przez Normana Johnsona , który jako pierwszy wymienił te wielościany w 1966 roku.
Pięciokątna gyrobicupola jest trzecią z nieskończonego zestawu gyrobicupola .
Pięciokątna żyrobiupola jest tym, co otrzymujesz, gdy weźmiesz rombicosidodecahedron , wytniesz środkowy parabidiminized rombicosidodecahedron ( J 80 ) i skleisz z powrotem dwie przeciwległe kopuły.
Formuły
Następujące wzory na objętość i pole powierzchni mogą być użyte, jeśli wszystkie ściany są regularne i mają długość krawędzi a :

