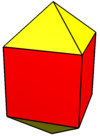
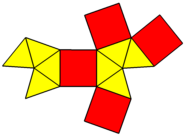
Wydłużona kwadratowa bipiramida

Wydłużona kwadratowa bipiramida
Typ	Johnson J 14 – J 15 – J 16
Twarze	8 trójkątów 4 kwadraty
Krawędzie	20
Wierzchołki	10
Konfiguracja wierzchołków	2(3 4 ) 8(3 2 .4 2 )
Grupa symetrii	D 4h , [4,2], (*422)
Grupa rotacyjna	re 4 , [4,2] + , (422)
Podwójny wielościan	Kwadratowe bifrustum
Nieruchomości	wypukły
Internet

Johnson stałe J ₁₅

W geometrii wydłużona kwadratowa bipiramida ( lub wydłużony ośmiościan ) jest jedną z brył Johnsona ( J ₁₅ ). Jak sama nazwa wskazuje, można go zbudować, wydłużając ośmiościan , wkładając sześcian między jego przystające połówki .

został nazwany kostką ołówkową lub kostką ołówkową o 12 ścianach .

Bryła Johnsona jest jednym z 92 ściśle wypukłych wielościanów , które składają się z regularnych ścian wielokątów, ale nie są jednolitymi wielościanami (to znaczy nie są bryłami platońskimi , bryłami Archimedesa , graniastosłupami ani antygraniastosłupami ). Zostały one nazwane przez Normana Johnsona , który jako pierwszy wymienił te wielościany w 1966 roku.

Kryształ cyrkonu jest przykładem wydłużonej kwadratowej bipiramidy.

Formuły

Następujące wzory na objętość ( $)$ , $)$ powierzchni ( i wysokość ( $)$ mogą być użyte, jeśli wszystkie są regularne , z długością krawędzi ${\ displaystyle$ :

${\ Displaystyle V = L ^ {3} \ cdot \ lewo (1 + {\ Frac {\ sqrt {2}} {3}} \ prawo) \ około L ^ {3} \ cdot 1,471404521}$

${\ Displaystyle A = L ^ {2} \ cdot \ lewo (4 + 2 {\ sqrt {3 }} \ prawej) \ około L ^ {2} \ cdot 7,464101615}$

${\ Displaystyle H = L \ cdot \ lewo (1 + {\ sqrt {2}} \ po prawej)\około L\cdot 2,414213562}$

Podwójny wielościan

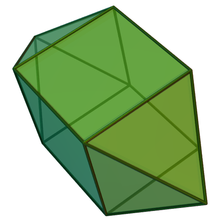
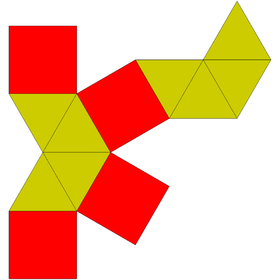
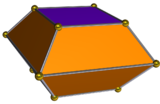
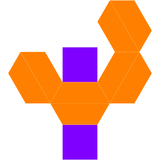
Podwójna wydłużonej kwadratowej bipiramidy nazywana jest kwadratowym bifrustum i ma 10 ścian: 8 trapezowych i 2 kwadratowe.

Podwójna wydłużona kwadratowa bipiramida	Sieć podwójnych

Powiązane wielościany i plastry miodu

Specjalny rodzaj wydłużonej kwadratowej bipiramidy bez wszystkich regularnych ścian umożliwia samoteselację przestrzeni euklidesowej. Trójkąty tej wydłużonej kwadratowej bipiramidy nie są regularne; mają krawędzie w stosunku 2: √ 3 : √ 3 .

Można to uznać za fazę przejściową między dwunastościennymi plastrami sześciennymi i rombowymi . Komórki są tutaj pokolorowane na biało, czerwono i niebiesko w oparciu o ich orientację w przestrzeni. Kwadratowe czapki piramid mają skrócone twarze trójkątów równoramiennych, przy czym sześć z tych piramid spotyka się razem, tworząc sześcian. Podwójność tego plastra miodu składa się z dwóch rodzajów ośmiościanów (ośmiościanów regularnych i antygraniastosłupów trójkątnych), utworzonych przez nałożenie ośmiościanów na kuboktaedry rektyfikowanego sześciennego plastra miodu . Oba plastry miodu mają symetrię [[4,3,4]].

Przekroje poprzeczne plastra miodu, przez środki komórek, tworzą fazowane płytki kwadratowe , ze spłaszczonymi sześciokątami poziomymi i pionowymi oraz kwadraty na prostopadłych wielościanach.

Plaster miodu

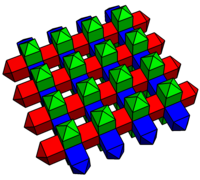Pół plastra miodu

Fazowane płytki kwadratowe

Przy regularnych ścianach wydłużona kwadratowa bipiramida może tworzyć teselację przestrzeni z czworościanami i ośmiościanami . (Ośmiościany można dalej rozłożyć na kwadratowe piramidy .) Ten plaster miodu można uznać za wydłużoną wersję czworościenno-ośmiościennego plastra miodu .

Zobacz też

• Wydłużona kwadratowa piramida

Linki zewnętrzne

• Eric W. Weisstein , Wydłużona kwadratowa bipiramida ( bryła Johnsona ) w MathWorld .