Plastyczność (fizyka)

„Materiał z tworzywa sztucznego” przekierowuje tutaj. Informacje na temat materiału użytego do produkcji można znaleźć w artykule Plastik .

Zobacz także: Deformacja (mechanika) i Deformacja (inżynieria)

Krzywa naprężenia-odkształcenia pokazująca typowe zachowanie plastyczności dla stopów nieżelaznych . ( Naprężenie , $odkształcenia$ jako funkcja $_$ ) _

1. Prawdziwa granica sprężystości
2. Granica proporcjonalności
3. Elastyczny limit
4. Przesunięcie granicy plastyczności

Krzywa naprężenia-odkształcenia typowa dla stali konstrukcyjnej .

---

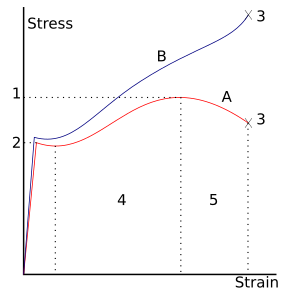
• 1: Najwyższa siła
• 2: Granica plastyczności (granica plastyczności)
• 3: Zerwanie
• 4: Obszar umocnienia przez odkształcenie
• 5: Region przewężenia
• Odp.: Naprężenie pozorne ( F / A ₀ )
• B: Rzeczywiste naprężenie ( F / A )

W fizyce i materiałoznawstwie plastyczność ( znana również jako odkształcenie plastyczne ) to zdolność materiału stałego do trwałego odkształcenia , czyli nieodwracalnej zmiany kształtu w odpowiedzi na przyłożone siły. Na przykład solidny kawałek metalu zginany lub wbijany w nowy kształt wykazuje plastyczność, ponieważ w samym materiale zachodzą trwałe zmiany. W inżynierii przejście od zachowania sprężystego do plastycznego znane jest jako plastyczność .

Odkształcenia plastyczne obserwuje się w większości materiałów, szczególnie w metalach , glebach , skałach , betonie i piankach . Jednakże mechanizmy fizyczne powodujące odkształcenie plastyczne mogą się znacznie różnić. W krystalicznej plastyczność metali jest zwykle konsekwencją dyslokacji . Takie defekty są stosunkowo rzadkie w większości materiałów krystalicznych, ale są liczne w niektórych i części ich struktury krystalicznej; w takich przypadkach może nastąpić krystaliczność plastyczna . W kruchym materiałów takich jak skała, beton i kość, plastyczność wynika głównie z poślizgu w miejscu mikropęknięć . W materiałach komórkowych, takich jak płynne pianki lub tkanki biologiczne , plastyczność jest głównie konsekwencją przegrupowania pęcherzyków lub komórek, zwłaszcza procesów T1 .

W przypadku wielu metali ciągliwych obciążenie rozciągające przyłożone do próbki powoduje, że zachowuje się ona w sposób elastyczny. Każdemu przyrostowi obciążenia towarzyszy proporcjonalny przyrost wydłużenia. Po usunięciu obciążenia element powraca do pierwotnego rozmiaru. Jednakże, gdy obciążenie przekroczy próg – granicę plastyczności – wydłużenie wzrasta szybciej niż w obszarze sprężystym; teraz, gdy obciążenie zostanie usunięte, pewien stopień rozciągnięcia pozostanie.

Odkształcenie sprężyste jest jednak przybliżone i jego jakość zależy od rozpatrywanego przedziału czasowego i prędkości ładowania. Jeżeli, jak wskazano na wykresie obok, odkształcenie obejmuje odkształcenie sprężyste, często określa się je również jako „odkształcenie sprężysto-plastyczne” lub „odkształcenie sprężysto-plastyczne”.

Doskonała plastyczność to właściwość materiałów, które poddają się nieodwracalnemu odkształceniu bez wzrostu naprężeń i obciążeń. Materiały z tworzyw sztucznych, które zostały utwardzone w wyniku wcześniejszego odkształcenia, takiego jak formowanie na zimno , mogą wymagać coraz większych naprężeń, aby dalej się odkształcać. Ogólnie rzecz biorąc, odkształcenie plastyczne zależy również od prędkości odkształcenia, tj. zwykle należy zastosować większe naprężenia, aby zwiększyć szybkość odkształcenia. Mówi się, że takie materiały odkształcają się lepko-plastycznie .

Właściwości przyczyniające się

Plastyczność materiału jest wprost proporcjonalna do plastyczności i plastyczności materiału.

Mechanizmy fizyczne

Plastyczność pod sferycznym nanowgłębnikiem w (111) miedzi. Wszystkie cząstki w idealnych pozycjach sieci są pomijane, a kod kolorystyczny odnosi się do pola naprężeń von Misesa.

W metalach

Plastyczność kryształu czystego metalu jest spowodowana przede wszystkim dwoma sposobami odkształcenia sieci krystalicznej: poślizgiem i bliźniakiem. Poślizg to odkształcenie ścinające, które przemieszcza atomy na wiele odległości międzyatomowych w stosunku do ich pozycji początkowej. Twinning to odkształcenie plastyczne, które zachodzi w dwóch płaszczyznach pod wpływem zestawu sił przyłożonych do danego elementu metalowego.

Większość metali wykazuje większą plastyczność na gorąco niż na zimno. Ołów wykazuje wystarczającą plastyczność w temperaturze pokojowej, podczas gdy żeliwo nie posiada wystarczającej plastyczności do jakiejkolwiek operacji kucia, nawet na gorąco. Właściwość ta ma znaczenie w operacjach formowania, kształtowania i wytłaczania metali. Większość metali staje się plastyczna poprzez ogrzewanie i dlatego jest kształtowana na gorąco.

Systemy poślizgowe

Główny artykuł: Poślizg (nauka o materiałach) § Systemy poślizgu

Materiały krystaliczne zawierają jednolite płaszczyzny atomów zorganizowane w sposób dalekiego zasięgu. Samoloty mogą ślizgać się obok siebie w ciasnych kierunkach, jak pokazano na stronie poświęconej systemom poślizgu. Efektem jest trwała zmiana kształtu w krysztale i odkształcenie plastyczne. Obecność dyslokacji zwiększa prawdopodobieństwo wystąpienia płaszczyzn.

Odwracalna plastyczność

W nanoskali pierwotne odkształcenie plastyczne prostych metali sześciennych skupionych na powierzchni jest odwracalne, o ile nie występuje transport materiału w postaci poślizgu poprzecznego . Stopy z pamięcią kształtu, takie jak drut nitinolowy, również wykazują odwracalną formę plastyczności, którą lepiej nazywa się pseudosprężystością .

Pasmo ścinające

Obecność innych defektów w krysztale może splątać dyslokacje lub w inny sposób uniemożliwić ich przesuwanie. Kiedy tak się dzieje, plastyczność jest zlokalizowana w określonych obszarach materiału. W przypadku kryształów te obszary o zlokalizowanej plastyczności nazywane są pasmami ścinania .

Mikroplastyczność

Mikroplastyczność jest zjawiskiem lokalnym w metalach. Dzieje się tak dla naprężeń , gdzie metal znajduje się globalnie w domenie sprężystej , podczas gdy niektóre obszary lokalne znajdują się w domenie plastycznej.

Materiały amorficzne

Szalenie

W przypadku materiałów amorficznych dyskusja na temat „dyslokacji” nie ma zastosowania, ponieważ całemu materiałowi brakuje uporządkowania dalekiego zasięgu. Materiały te mogą nadal ulegać odkształceniom plastycznym. Ponieważ materiały amorficzne, takie jak polimery, nie są dobrze uporządkowane, zawierają dużą ilość wolnej objętości lub zmarnowanej przestrzeni. Ciągnięcie tych materiałów w napięciu otwiera te obszary i może nadać materiałom zamglony wygląd. To zmętnienie jest wynikiem pękania , podczas którego w materiale tworzą się włókienka w obszarach o dużym naprężeniu hydrostatycznym . Materiał może przejść od uporządkowanego wyglądu do „szalonego” wzoru naprężeń i rozstępów.

Materiały komórkowe

Materiały te odkształcają się plastycznie, gdy moment zginający przekroczy moment w pełni plastyczny. Dotyczy to pianek otwartokomórkowych, w których moment zginający działa na ścianki komórek. Pianki mogą być wykonane z dowolnego materiału o granicy plastyczności, w tym ze sztywnych polimerów i metali. Ta metoda modelowania pianki w postaci belek ma zastosowanie tylko wtedy, gdy stosunek gęstości pianki do gęstości materii jest mniejszy niż 0,3. Dzieje się tak dlatego, że belki uginają się osiowo, a nie zginają. W piankach o zamkniętych komórkach granica plastyczności wzrasta, jeśli materiał jest naprężony z powodu membrany rozciągającej się na powierzchni komórek.

Gleby i piasek

Główny artykuł: mechanika gleby w stanie krytycznym

Gleby, zwłaszcza iły, wykazują znaczną nieelastyczność pod obciążeniem. Przyczyny plastyczności gleb mogą być dość złożone i silnie zależne od mikrostruktury , składu chemicznego i zawartości wody. Plastyczne zachowanie gruntów spowodowane jest przede wszystkim przemieszczeniem skupisk sąsiadujących ze sobą ziaren.

Skały i beton

Główny artykuł: plastyczność górotworu

Odkształcenia niesprężyste skał i betonu spowodowane są przede wszystkim powstawaniem mikropęknięć i ruchami ślizgowymi względem tych pęknięć. W wysokich temperaturach i ciśnieniach na zachowanie plastyczne może wpływać również ruch dyslokacji w poszczególnych ziarnach mikrostruktury.

Niezależne od czasu plastyczność i płynięcie plastyczne w materiałach krystalicznych

Niezależny od czasu płynięcie plastyczne zarówno w monokryształach, jak i polikryształach jest definiowane przez krytyczne/maksymalne rozwiązane naprężenie ścinające ( τ _CRSS ), inicjujące migrację dyslokacji wzdłuż równoległych płaszczyzn poślizgu pojedynczego układu poślizgu, definiując w ten sposób przejście od zachowania odkształcenia sprężystego do plastycznego w materiały krystaliczne.

Niezależne od czasu plastyczność i płynięcie plastyczne w monokryształach

Krytyczne rozwiązane naprężenie ścinające dla monokryształów jest określone przez prawo Schmida τ _CRSS = σ _y /m, gdzie σ _y jest granicą plastyczności monokryształu, a m jest współczynnikiem Schmida. Współczynnik Schmida składa się z dwóch zmiennych λ i φ, określających odpowiednio kąt między kierunkiem płaszczyzny poślizgu a przyłożoną siłą rozciągającą oraz kąt między normalną płaszczyzny poślizgu a przyłożoną siłą rozciągającą. Warto zauważyć, że m > 1, σ _y > τ _CRSS .

Krytycznie rozwiązano zależność naprężenia ścinającego od temperatury, szybkości odkształcania i defektów punktowych

Trzy charakterystyczne obszary krytycznego rozdzielonego naprężenia ścinającego w funkcji temperatury.

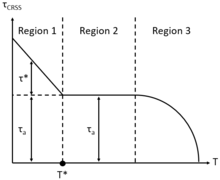
Istnieją trzy charakterystyczne obszary krytycznego rozwiązanego naprężenia ścinającego w funkcji temperatury. W obszarze niskiej temperatury 1 ( T ≤ 0,25 T _m ) szybkość odkształcenia έ musi być wysoka, aby osiągnąć wysoki τ _CRSS , który jest wymagany do zainicjowania poślizgu dyslokacyjnego i równoważnego przepływu plastycznego. W obszarze 1 krytyczne rozwiązane naprężenie ścinające ma dwie składowe: atermiczną ( τ _a ) i termiczną ( τ *) odpowiednio naprężenia styczne, wynikające z naprężenia niezbędnego do przemieszczenia dyslokacji w obecności innych dyslokacji oraz odporność defektów punktowych na przeszkodę w migracji dyslokacji. Dla T = T * zdefiniowany jest obszar umiarkowanej temperatury 2 (0,25 T _m < T < 0,7 T _m ), w którym składowa termicznego naprężenia ścinającego τ * → 0, reprezentuje eliminację impedancji defektu punktowego do migracji dyslokacji. Zatem niezależne od temperatury krytyczne rozwiązane naprężenie ścinające τ _CRSS = τ _a pozostaje takie do momentu zdefiniowania obszaru 3. Warto zauważyć, że w obszarze 2 umiarkowanej temperatury należy wziąć pod uwagę zależne od czasu mechanizmy odkształcenia plastycznego (pełzania), takie jak opór substancji rozpuszczonej. Co więcej, w obszarze wysokiej temperatury 3 ( T ≥ 0,7 T _m ) έ może być niskie, przyczyniając się do niskiego τ _CRSS , jednakże płynięcie plastyczne nadal będzie występować z powodu aktywowanych termicznie, zależnych od czasu mechanizmów odkształcenia plastycznego w wysokiej temperaturze, takich jak Nabarro – Śledź ( NH) i przepływ dyfuzyjny Coble'a odpowiednio przez sieć i wzdłuż powierzchni monokryształu, a także pełzanie wznoszenia i ślizgania dyslokacji.

Etapy niezależnego od czasu płynięcia plastycznego, po plastyczności

Trzy etapy niezależnego od czasu odkształcenia plastycznego monokryształów.

Podczas pierwszego etapu łatwego poślizgu szybkość umocnienia przez zgniot, określona przez zmianę naprężenia ścinającego w odniesieniu do odkształcenia ścinającego ( dτ / dγ ) jest niska, reprezentatywna dla małej ilości przyłożonego naprężenia ścinającego niezbędnego do wywołania dużej ilości odkształcenia ścinającego. Łatwy poślizg dyslokacji i odpowiadający mu przepływ przypisuje się migracji dyslokacji tylko wzdłuż równoległych płaszczyzn poślizgu (tj. jednego systemu poślizgu). Wykazuje się umiarkowaną impedancję migracji dyslokacji wzdłuż równoległych płaszczyzn poślizgu, zgodnie z oddziaływaniami słabego pola naprężenia między tymi dyslokacjami, które zwiększają się wraz z mniejszymi odstępami międzypłaszczyznowymi. Ogólnie rzecz biorąc, te migrujące dyslokacje w obrębie pojedynczego układu poślizgu działają jak słabe przeszkody dla przepływu i obserwuje się niewielki wzrost naprężenia w porównaniu z granicą plastyczności. Podczas etapu 2 liniowego utwardzania przepływu, szybkość utwardzania przez zgniot staje się wysoka, ponieważ wymagane jest znaczne naprężenie, aby przezwyciężyć interakcje pola naprężeń dyslokacji migrujących w nierównoległych płaszczyznach poślizgu (tj. wielokrotnych systemów poślizgu), działając jako silne przeszkody dla przepływu. Aby wywołać ciągłą migrację dyslokacji w przypadku małych odkształceń, wymagany jest duży stres. Naprężenie przepływu ścinającego jest wprost proporcjonalne do pierwiastka kwadratowego gęstości dyslokacji (τ _przepływ ~ ρ ^½ ), niezależnie od ewolucji konfiguracji dyslokacji, wykazując zależność hartowania od liczby obecnych dyslokacji. Jeśli chodzi o tę ewolucję konfiguracji dyslokacji, przy małych odkształceniach układ dyslokacji jest losowym trójwymiarowym układem przecinających się linii. Odkształcenia umiarkowane odpowiadają strukturom dyslokacji komórkowych o niejednorodnym rozkładzie dyslokacji, z dużą gęstością dyslokacji na granicach komórek i małą gęstością dyslokacji wewnątrz komórki. Przy jeszcze większych odkształceniach struktura dyslokacji komórkowej zmniejsza się, aż do osiągnięcia rozmiaru minimalnego. Wreszcie, szybkość utwardzania przez zgniot staje się ponownie niska w etapie wyczerpania/nasycenia utwardzania 3 płynięcia tworzywa sztucznego, ponieważ małe naprężenia ścinające powodują duże odkształcenia ścinające. Warto zauważyć, że przypadki, w których wiele systemów poślizgu jest zorientowanych korzystnie pod względem przyłożonego naprężenia, τ _CRSS dla tych układów może być podobny, a plastyczność może wystąpić w zależności od migracji dyslokacji wzdłuż wielu układów poślizgu z nierównoległymi płaszczyznami poślizgu, wykazując szybkość utwardzania przez zgniot w etapie 1, typowo charakterystyczną dla etapu 2. Wreszcie, rozróżnienie pomiędzy niezależnym od czasu odkształceniem plastycznym w sześcienne metale przejściowe centrowane na ciele i metale sześcienne centrowane na powierzchni podsumowano poniżej.

Porównanie niezależnego od czasu odkształcenia plastycznego sześciennych metali przejściowych skupionych wokół ciała i metali sześciennych skupionych na powierzchni, podkreślając krytyczne rozwiązane naprężenie ścinające, szybkość utwardzania przez zgniot i odkształcenie przewężające podczas próby rozciągania.

Sześcienne metale przejściowe skupione na ciele	Metale sześcienne skupione na twarzy
Krytyczne rozwiązane naprężenie ścinające = wysokie (względnie) i silnie zależne od temperatury	Krytyczne rozwiązane naprężenie ścinające = niskie (względnie) i słabo zależne od temperatury
Szybkość utwardzania przez zgniot = niezależna od temperatury	Szybkość utwardzania przez zgniot = zależna od temperatury
Naprężenie szyi wzrasta wraz z temperaturą	Odkształcenie szyi zmniejsza się wraz z temperaturą

Niezależne od czasu uplastycznienie i płynięcie plastyczne w polikryształach

Plastyczność w polikryształach różni się zasadniczo od monokryształów ze względu na obecność płaskich defektów na granicach ziaren (GB), które stanowią bardzo silną przeszkodę w przepływie plastycznym, utrudniając migrację dyslokacji na całej długości aktywowanej(-ych) płaszczyzn poślizgu. Dlatego dyslokacje nie mogą przechodzić z jednego ziarna do drugiego przez granicę ziaren. W poniższych sekcjach omówiono specyficzne wymagania GB dotyczące rozległego odkształcenia plastycznego polikryształów przed pęknięciem, a także wpływ plastyczności mikroskopowej w obrębie poszczególnych krystalitów na plastyczność makroskopową polikryształu. Krytyczne rozwiązane naprężenie ścinające dla polikryształów jest również określone przez prawo Schmida (τ _CRSS = σ _y /ṁ), gdzie σ _y to granica plastyczności polikryształu, a ṁ to ważony współczynnik Schmida. Ważony współczynnik Schmida odzwierciedla najmniej korzystnie zorientowany system poślizgu spośród najkorzystniej zorientowanych systemów poślizgu ziaren tworzących GB.

Więzy graniczne ziaren w polikryształach

Ograniczenie GB dla polikryształów można wyjaśnić, biorąc pod uwagę granicę ziaren w płaszczyźnie xz pomiędzy dwoma monokryształami A i B o identycznym składzie, strukturze i układach poślizgu, ale źle zorientowanych względem siebie. Aby zapewnić, że pomiędzy indywidualnie odkształcającymi się ziarnami nie utworzą się puste przestrzenie, ograniczenie GB dla bikryształu jest następujące: ε _xx ^A = ε _xx ^B (odkształcenie osiowe x w GB musi być równoważne dla A i B), ε _zz ^A = ε _zz ^B (odkształcenie osiowe z w GB musi być równoważne dla A i B) oraz ε _xz ^A = ε _xz ^B (odkształcenie ścinające xz wzdłuż płaszczyzny xz-GB musi być równoważne dla A i B). Ponadto to ograniczenie GB wymaga aktywacji pięciu niezależnych systemów poślizgu na krystalit tworzący GB. Warto zauważyć, że ponieważ niezależne systemy poślizgu definiuje się jako płaszczyzny poślizgu, na których migracje dyslokacji nie mogą być odtworzone przez żadną kombinację migracji dyslokacji wzdłuż innych płaszczyzn systemu poślizgu, liczba geometrycznych systemów poślizgu dla danego układu kryształów - które z definicji mogą być zbudowane przez poślizg kombinacji systemów – jest zazwyczaj większa niż w przypadku niezależnych systemów poślizgu. Co istotne, dla każdego z siedmiu układów krystalicznych istnieje maksymalnie pięć niezależnych systemów poślizgu, jednak nie wszystkie siedem systemów krystalicznych osiąga tę górną granicę. Faktycznie, nawet w obrębie danego układu krystalicznego skład i sieć Bravais'a różnicują liczbę niezależnych układów poślizgowych (patrz tabela poniżej). W przypadkach, w których krystality polikryształu nie uzyskują pięciu niezależnych układów poślizgu, warunek GB nie może zostać spełniony, a zatem niezależne od czasu odkształcenie poszczególnych krystalitów powoduje pęknięcia i puste przestrzenie na GB polikryształu i wkrótce następuje pęknięcie . Zatem dla danego składu i struktury monokryształ posiadający mniej niż pięć niezależnych układów poślizgowych jest silniejszy (wykazuje większy stopień plastyczności) niż jego postać polikrystaliczna.

Liczba niezależnych systemów poślizgu dla danego składu (podstawowa klasa materiału) i konstrukcji (krata Bravais).

Siatka Bravais’go	Podstawowa klasa materiału: # Niezależne systemy poślizgowe
Twarz wyśrodkowana sześciennie	Metal: 5, ceramika (kowalencyjna): 5, ceramika (jonowa): 2
Korpus wyśrodkowany sześciennie	Metal: 5
Prosty sześcienny	Ceramika (jonowa): 3
Sześciokątny	Metal: 2, ceramika (mieszana): 2

Konsekwencje ograniczeń granic ziaren w polikryształach

Chociaż dwa krystality A i B omówione w powyższej sekcji mają identyczne układy poślizgu, są one źle zorientowane względem siebie, a zatem źle zorientowane pod względem przyłożonej siły. Zatem mikroskopijne ustępowanie we wnętrzu krystalitu może zachodzić zgodnie z zasadami rządzącymi otrzymywaniem monokryształu niezależnym od czasu. Ostatecznie aktywowane płaszczyzny poślizgu we wnętrzach ziaren umożliwią migrację dyslokacji do GB, gdzie wiele dyslokacji gromadzi się następnie jako dyslokacje niezbędne geometrycznie. To spiętrzenie odpowiada gradientom odkształceń w poszczególnych ziarnach, ponieważ gęstość dyslokacji w pobliżu GB jest większa niż we wnętrzu ziaren, powodując naprężenie na stykające się sąsiednie ziarna. Rozważając bikryształ AB jako całość, najkorzystniej zorientowanym systemem poślizgu w A nie będzie ten w B, a zatem τ ^A _CRSS ≠ τ ^B _CRSS . Najważniejszy jest fakt, że makroskopowe plastyczność bikryształu wydłuża się aż do osiągnięcia wyższej wartości τ _{CRSS pomiędzy ziarnami A i B, zgodnie z ograniczeniem GB.} Zatem dla danego składu i struktury polikryształ z pięcioma niezależnymi układami poślizgu jest silniejszy (większy stopień plastyczności) niż jego postać monokrystaliczna. Odpowiednio, szybkość utwardzania przez zgniot będzie wyższa dla polikryształu niż dla monokryształu, ponieważ w polikrysztale wymagane jest większe naprężenie, aby wytworzyć odkształcenia. Co ważne, podobnie jak w przypadku naprężenia przepływu monokryształu, _{przepływ τ} ~ρ ^½ , ale jest też odwrotnie proporcjonalna do pierwiastka kwadratowego ze średniej średnicy ziarna (τ _przepływ ~d ^-½ ). Dlatego naprężenie płynięcia polikryształu, a tym samym jego wytrzymałość, wzrasta wraz z małym rozmiarem ziaren. Powodem tego jest to, że mniejsze ziarna mają stosunkowo mniejszą liczbę płaszczyzn poślizgu do aktywacji, co odpowiada mniejszej liczbie dyslokacji migrujących do GB, a zatem mniejszym naprężeniom wywoływanym na sąsiednich ziarnach w wyniku spiętrzenia dyslokacji. Ponadto dla danej objętości polikryształu mniejsze ziarna stanowią silniejszą granicę ziaren stanowiącą przeszkodę. Te dwa czynniki pozwalają zrozumieć, dlaczego początek makroskopowego przepływu w drobnoziarnistych polikryształach następuje przy większych przyłożonych naprężeniach niż w gruboziarnistych polikryształach.

Opisy matematyczne

Teoria deformacji

Wyidealizowana jednoosiowa krzywa naprężenia-odkształcenia przedstawiająca reżimy odkształcenia sprężystego i plastycznego dla teorii odkształceń plastyczności

Istnieje kilka matematycznych opisów plastyczności. Jedną z nich jest teoria deformacji (patrz np. prawo Hooke'a ), w której tensor naprężenia Cauchy'ego (rzędu d-1 w wymiarach d) jest funkcją tensora odkształcenia. Chociaż opis ten jest dokładny, gdy niewielka część materii poddawana jest rosnącemu obciążeniu (takemu jak obciążenie odkształceniowe), teoria ta nie może wyjaśnić nieodwracalności.

Materiały plastyczne mogą wytrzymać duże odkształcenia plastyczne bez pękania . Jednak nawet metale plastyczne pękają, gdy odkształcenie stanie się wystarczająco duże - dzieje się to w wyniku umocnienia materiału, co powoduje, że staje się on kruchy . Obróbka cieplna , taka jak wyżarzanie , może przywrócić plastyczność obrabianego przedmiotu, dzięki czemu można kontynuować kształtowanie.

Teoria plastyczności przepływu

Główny artykuł: Teoria plastyczności przepływu

W 1934 roku Egon Orowan , Michael Polanyi i Geoffrey Ingram Taylor , mniej więcej jednocześnie, zdali sobie sprawę, że odkształcenie plastyczne materiałów ciągliwych można wyjaśnić w kategoriach teorii dyslokacji . Matematyczna teoria plastyczności, teoria plastyczności płynięcia , wykorzystuje zbiór nieliniowych, niecałkowalnych równań do opisania zbioru zmian odkształcenia i naprężenia w stosunku do stanu poprzedniego oraz niewielkiego wzrostu odkształcenia.

Kryteria wydajności

Porównanie kryterium Treski z kryterium Von Misesa

Główny artykuł: Wydajność (inżynieria)

Jeśli naprężenie przekroczy wartość krytyczną, jak wspomniano powyżej, materiał ulegnie plastycznemu, czyli nieodwracalnemu odkształceniu. To krytyczne naprężenie może mieć charakter rozciągający lub ściskający. Do określenia, czy materiał ustąpił, powszechnie stosuje się kryteria Tresca i von Misesa . Jednakże kryteria te okazały się niewystarczające w przypadku dużej gamy materiałów, a kilka innych kryteriów plastyczności jest również w powszechnym użyciu.

Kryterium Treski

Kryterium Tresca opiera się na założeniu, że gdy materiał zawodzi, dzieje się to pod wpływem ścinania, co jest stosunkowo dobrym założeniem w przypadku metali. Biorąc pod uwagę główny stan naprężenia, możemy użyć koła Mohra do obliczenia maksymalnych naprężeń ścinających, jakich doświadcza nasz materiał i stwierdzić, że materiał ulegnie zniszczeniu, jeśli

${\ Displaystyle \ sigma _ {1} - \ sigma _ {3} \ geq \ sigma _ {0}}$

₀ gdzie σ ₁ to maksymalne naprężenie normalne, σ ₃ to minimalne naprężenie normalne, a σ to naprężenie, pod którym materiał ulega zniszczeniu przy obciążeniu jednoosiowym. Można skonstruować powierzchnię plastyczności, która stanowi wizualną reprezentację tej koncepcji . Wewnątrz powierzchni plastyczności odkształcenie jest sprężyste. Na powierzchni odkształcenie jest plastyczne. Niemożliwe jest, aby materiał miał stany naprężenia poza powierzchnią plastyczności.

Kryterium Hubera–von Misesa

Powierzchnie plastyczności von Misesa we współrzędnych głównych naprężeń otaczają cylinder wokół osi hydrostatycznej. Pokazano także sześciokątną powierzchnię plastyczności Treski .

Główny artykuł: kryterium wydajności von Misesa

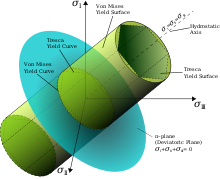
Kryterium Hubera – von Misesa opiera się na kryterium Tresca, ale uwzględnia założenie, że naprężenia hydrostatyczne nie przyczyniają się do zniszczenia materiału. MT Huber jako pierwszy zaproponował kryterium energii ścinania. Von Mises oblicza efektywne naprężenie przy obciążeniu jednoosiowym, odejmując naprężenia hydrostatyczne i stwierdza, że ​​wszystkie naprężenia efektywne większe niż te, które powodują uszkodzenie materiału przy obciążeniu jednoosiowym, spowodują odkształcenie plastyczne.

${\ Displaystyle \ sigma _ {v} ^ {2} = {\ tfrac {1} {2}} [(\ sigma _ {11} - \ sigma _ {22}) ^ {2} + (\ sigma _ { 22}-\sigma _{33})^{2}+(\sigma _{11}-\sigma _{33})^{2}+6(\sigma _{23}^{2}+\sigma _{31}^{2}+\sigma _{12}^{2})]}$

Ponownie, wizualną reprezentację powierzchni plastyczności można skonstruować przy użyciu powyższego równania, które przyjmuje kształt elipsy. Wewnątrz powierzchni materiały ulegają odkształceniu sprężystemu. Dotarcie do powierzchni powoduje, że materiał ulega odkształceniom plastycznym.

Zobacz też

• Granice Atterberga
• Plastometr
• Współczynnik Poissona

Dalsza lektura

•   Ashby, MF (2001). „Odkształcenie plastyczne materiałów komórkowych”. Encyklopedia materiałów: nauka i technologia . Tom. 7. Oksford: Elsevier. s. 7068–7071. ISBN 0-08-043152-6 .
•   Han, W.; Reddy, BD (2013). Plastyczność: teoria matematyczna i analiza numeryczna (wyd. 2). Nowy Jork: Springer. ISBN 978-1-4614-5939-2 .
•   Kaczanow, LM (2004). Podstawy teorii plastyczności . Książki Dover. ISBN 0-486-43583-0 .
•   Khan, AS; Huang, S. (1995). Ciągła teoria plastyczności . Wiley’a. ISBN 0-471-31043-3 .
•   Simo, JC; Hughes, TJ (1998). Niesprężystość obliczeniowa . Skoczek. ISBN 0-387-97520-9 .
• Van Vliet, KJ (2006). „Zachowanie mechaniczne materiałów” . Numer kursu MIT 3.032 . Instytut Technologii w Massachusetts.