Naprężenie ścinające

Naprężenie ścinające
Wspólne symbole	τ
jednostka SI	pascal
Pochodne z innych wielkości	τ = F / A

Siła ścinająca jest przykładana do górnej części prostokąta, podczas gdy dolna część jest utrzymywana na miejscu. Powstałe naprężenie ścinające τ deformuje prostokąt w równoległobok . Zaangażowany obszar byłby wierzchołkiem równoległoboku.

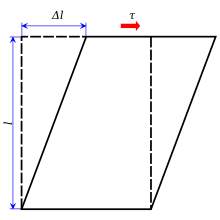
Naprężenie ścinające (często oznaczane przez τ ( greckie : tau )) jest składową naprężenia współpłaszczyznowego z przekrojem poprzecznym materiału . Wynika to z siły ścinającej , składowej wektora siły równoległej do przekroju poprzecznego materiału. Z drugiej strony naprężenie normalne wynika ze składowej wektora siły prostopadłej do przekroju poprzecznego materiału, na który działa.

Ogólne naprężenie ścinające

Wzór na obliczenie średniego naprężenia ścinającego to siła na jednostkę powierzchni.:

${\ Displaystyle \ tau = {F \ nad A},}$

Gdzie:

τ = naprężenie ścinające;

F = zastosowana siła;

A = pole przekroju poprzecznego materiału o polu równoległym do wektora przyłożonej siły.

Inne formy

Naprężenie ścinające ściany

Naprężenie ścinające ściany wyraża siłę opóźniającą (na jednostkę powierzchni) ze ściany w warstwach płynu przepływającego obok ściany. Jest zdefiniowany jako:

${\ Displaystyle \ tau _ {w}: = \ mu \ lewo ({\ Frac {\ częściowe u} {\ częściowe y}} \ prawej) _ {y = 0}}$

Gdzie $lepkość$ dynamiczna , prędkość $odległość$$i$ od .

Stosowany jest np. w opisie przepływu krwi tętniczej , w którym to przypadku istnieją dowody na to, że wpływa na proces aterogenny .

Czysty

Czyste naprężenie ścinające jest powiązane z czystym odkształceniem ścinającym , oznaczonym jako γ , za pomocą następującego równania:

${\ Displaystyle \ tau = \ gamma G \,}$

gdzie G jest modułem ścinania materiału izotropowego , określonym wzorem

${\ Displaystyle G = {\ Frac {E} {2 (1 + \ nu)}}.}$

Tutaj E jest modułem Younga , a v jest współczynnikiem Poissona .

Ścinanie belki

Ścinanie belki definiuje się jako wewnętrzne naprężenie ścinające belki spowodowane siłą ścinającą przyłożoną do belki.

${\ Displaystyle \ tau: = {fQ \ nad Ib},}$

Gdzie

f = całkowita siła ścinająca w danym miejscu;

Q = statyczny moment powierzchni ;

b = grubość (szerokość) w materiale prostopadła do ścinania;

I = moment bezwładności całego pola przekroju poprzecznego.

Wzór na ścinanie belki jest również znany jako wzór naprężenia ścinającego Żurawskiego na cześć Dymitra Iwanowicza Żurawskiego , który wyprowadził go w 1855 roku.

Ścinanie półskorupowe

Dalsze informacje: Przepływ ścinający

Naprężenia ścinające w konstrukcji półskorupowej można obliczyć, idealizując przekrój poprzeczny konstrukcji na zestaw podłużnic (przenoszących tylko obciążenia osiowe) i środników (przenoszących tylko przepływy ścinające ). Dzielenie przepływu ścinającego przez grubość danej części struktury półskorupowej daje naprężenie ścinające. Zatem maksymalne naprężenie ścinające wystąpi albo we wstędze o maksymalnym przepływie ścinającym, albo we wstędze o minimalnej grubości

Konstrukcje w glebie mogą również zawieść z powodu ścinania; np . ciężar wypełnionej ziemią tamy lub grobli może spowodować zawalenie się podłoża, jak małe osuwisko .

Ścinanie udarowe

Maksymalne naprężenie ścinające powstające w litym okrągłym pręcie poddanym uderzeniu wyraża się równaniem:

${\ Displaystyle \ tau = {\ sqrt {2UG \ ponad V}},}$

Gdzie

U = zmiana energii kinetycznej;

G = moduł ścinania ;

V = objętość pręta;

I

U = U _{obracający się} + U _zastosowany ;

U _obracanie = 1 / 2 Iω ² ;

U _zastosowany = Tθ _przesunięty ;

I = masowy moment bezwładności;

ω = prędkość kątowa.

Naprężenia ścinające w płynach

Zobacz też: lepkość , płynięcie Couette'a , równanie Hagena-Poiseuille'a , iloczyn głębokości i nachylenia i proste ścinanie

Wszelkie rzeczywiste płyny ( w tym ciecze i gazy ) poruszające się wzdłuż stałej granicy będą podlegały naprężeniu ścinającemu na tej granicy. Warunek braku poślizgu oznacza, że ​​prędkość płynu na granicy (względem granicy) wynosi zero; chociaż na pewnej wysokości od granicy prędkość przepływu musi być równa prędkości płynu. Obszar między tymi dwoma punktami nazywany jest warstwą graniczną . Dla wszystkich płynów newtonowskich w przepływie laminarnym naprężenie ścinające jest proporcjonalne do szybkości odkształcania w płynie, gdzie lepkość jest stałą proporcjonalności. W przypadku płynów nienewtonowskich lepkość nie jest stała. Naprężenie ścinające jest przenoszone na granicę w wyniku tej utraty prędkości.

W przypadku płynu newtonowskiego naprężenie ścinające w elemencie powierzchniowym równoległym do płaskiej płyty w punkcie y jest określone wzorem:

${\ Displaystyle \ tau (y) = \ mu {\ Frac {\ częściowe u} {\ częściowe y}}}$

Gdzie

μ to lepkość dynamiczna przepływu;

u jest prędkością przepływu wzdłuż granicy;

y to wysokość nad granicą.

W szczególności naprężenie ścinające ściany definiuje się jako:

${\ Displaystyle \ tau _ {\ operatorname {w}}: = \ tau (y = 0) = \ mu \ lewo. {\ Frac {\ częściowe u} {\ częściowe y}} \ prawo | _ {y = 0 }~~.}$

Prawo konstytutywne Newtona dla dowolnej ogólnej geometrii (w tym wspomnianej powyżej płaskiej płyty) stwierdza, że ​​tensor ścinania (tensor drugiego rzędu) jest proporcjonalny do gradientu prędkości przepływu (prędkość jest wektorem, więc jej gradient jest drugiego rzędu napinacz):

${\ Displaystyle {\ overset {\ strzałka w lewo} {\ tau}} ({\ vec {u}}) = \ mu {\ vec {\ nabla}}} {\ vec {u}}}$

a stała proporcjonalności nazywana jest lepkością dynamiczną . Dla izotropowego przepływu Newtona jest to skalar, podczas gdy dla anizotropowego przepływu Newtona może to być również tensor drugiego rzędu. Podstawowym aspektem jest to, że dla płynu newtonowskiego lepkość dynamiczna jest niezależna od prędkości przepływu (tj. prawo konstytutywne naprężenia ścinającego jest liniowe ), podczas gdy dla przepływów nienewtonowskich nie jest to prawdą i należy uwzględnić modyfikację:

${\ Displaystyle {\ overset {\ strzałka w lewo} {\ tau}} ({\ vec {u}}) = \ mu ({\ vec {u} }){\vec {\nabla}}{\vec {u}}}$

To już nie jest prawo Newtona, ale ogólna tożsamość tensoryczna: zawsze można znaleźć wyrażenie lepkości jako funkcję prędkości przepływu, biorąc pod uwagę dowolne wyrażenie naprężenia ścinającego jako funkcję prędkości przepływu. Z drugiej strony, biorąc pod uwagę naprężenie ścinające jako funkcję prędkości przepływu, reprezentuje przepływ newtonowski tylko wtedy, gdy można go wyrazić jako stałą gradientu prędkości przepływu. Stałą, którą można znaleźć w tym przypadku, jest dynamiczna lepkość przepływu.

Przykład

Biorąc pod uwagę przestrzeń 2D we współrzędnych kartezjańskich (x,y) (składowe prędkości przepływu to odpowiednio (u,v)), wówczas macierz naprężeń ścinających określona wzorem:

${\ Displaystyle {\ rozpocząć {pmatrix} \ tau _ {xx} i \ tau _ {xy} \\\tau _{yx}&\tau _{yy}\end{pmatrix}}={\begin{pmatrix}x{\frac {\częściowe u}{\częściowe x}}&0\\0&-t{ \frac {\częściowy v}{\częściowy y}}\end{pmatrix}}}$

reprezentuje przepływ Newtona, w rzeczywistości można go wyrazić jako:

${\ Displaystyle {\ rozpocząć {pmatrix} \ tau _ {xx} i \ tau _ {xy} \\\ tau _ {yx} i \ tau _ {yy} \ koniec {pmatrix}} = {\ rozpocząć {pmatrix} x&0\\0&-t\end{pmatrix}}\cdot {\begin{pmatrix}{\frac {\częściowe u}}{\częściowe x}}&{\frac {\częściowe u}{\częściowe y}}\ \{\frac {\częściowy v}{\częściowy x}}&{\frac {\częściowy v}{\częściowy y}}\end{pmatrix}}}$ ,

tj. przepływ anizotropowy z tensorem lepkości:

${\ Displaystyle {\ rozpocząć {pmatrix} \ mu _ {xx} i \ mu _ {xy} \\\ mu _ {yx} &\mu _{yy}\end{pmatrix}}={\begin{pmatrix}x&0\\0&-t\end{pmatrix}}}$

która jest niejednorodna (zależy od współrzędnych przestrzennych) i przejściowa, ale odpowiednio jest niezależna od prędkości przepływu:

${\ Displaystyle {\ overset {\ strzałka w lewo} {\ mu}} (x, t) = {\ rozpocząć {pmatrix} x & 0 \\ 0 i - t \ koniec {pmatrix }}}$

Ten przepływ jest zatem newtonowski. Z drugiej strony przepływ, w którym lepkości były:

${\ Displaystyle {\ rozpocząć {pmatrix} \ mu _ {xx} i \ mu _ {xy} \\\ mu _ {yx }&\mu _{yy}\end{pmatrix}}={\begin{pmatrix}{\frac {1}{u}}&0\\0&{\frac {1}{u}}\end{pmatrix} }}$

jest nienewtonowskie, ponieważ lepkość zależy od prędkości przepływu. Ten nienewtonowski przepływ jest izotropowy (macierz jest proporcjonalna do macierzy tożsamości), więc lepkość jest po prostu skalarem:

${\ Displaystyle \ mu (u) = {\ Frac {1} {u}}}$

Pomiar za pomocą czujników

Czujnik naprężenia ścinającego rozbieżnych prążków

Zależność tę można wykorzystać do pomiaru naprężenia ścinającego ściany. Gdyby czujnik mógł bezpośrednio zmierzyć gradient profilu prędkości na ścianie, wówczas pomnożenie przez lepkość dynamiczną dałoby naprężenie ścinające. Taki czujnik zademonstrowali AA Naqwi i WC Reynolds. Wzór interferencyjny generowany przez wysłanie wiązki światła przez dwie równoległe szczeliny tworzy sieć liniowo rozbieżnych prążków, które wydają się pochodzić z płaszczyzny dwóch szczelin (patrz eksperyment z podwójną szczeliną ). Gdy cząsteczka w płynie przechodzi przez prążki, odbiornik wykrywa odbicie wzoru prążków. Sygnał można przetwarzać, a znając kąt prążków, można ekstrapolować wysokość i prędkość cząstki. Zmierzona wartość gradientu prędkości ścianki jest niezależna od właściwości płynu iw rezultacie nie wymaga kalibracji. Ostatnie postępy w technologiach wytwarzania mikrooptyki umożliwiły wykorzystanie zintegrowanego dyfrakcyjnego elementu optycznego do wytworzenia czujników naprężenia ścinającego z rozbieżnymi prążkami, które można stosować zarówno w powietrzu, jak iw cieczy.

Czujnik naprężenia ścinającego z mikrokolumną

Kolejną techniką pomiarową są smukłe, montowane na ścianie mikrosłupy wykonane z elastycznego polimeru PDMS, które wyginają się w reakcji na przyłożone siły oporu w pobliżu ściany. Czujnik należy zatem do zasad pomiaru pośredniego, opierających się na zależności między gradientami prędkości przy ścianie a lokalnym naprężeniem ścinającym przy ścianie.

Metoda elektrodyfuzyjna

Metoda Electro-Diffusional mierzy szybkość ścinania ścianki w fazie ciekłej z mikroelektrody w warunkach ograniczonego prądu dyfuzyjnego. Różnica potencjałów między anodą o dużej powierzchni (najczęściej znajdującą się daleko od obszaru pomiarowego) a małą elektrodą roboczą pełniącą rolę katody prowadzi do szybkiej reakcji redoks. Zanik jonów następuje tylko na powierzchni aktywnej mikrosondy, powodując powstanie dyfuzyjnej warstwy granicznej, w której szybkość reakcji elektrodyfuzji jest kontrolowana wyłącznie przez dyfuzję. Rozwiązanie równania konwekcyjno-dyfuzyjnego w obszarze przyściennym mikroelektrody prowadzi do rozwiązań analitycznych opartych na długości charakterystycznej mikrosond, właściwościach dyfuzyjnych roztworu elektrochemicznego i szybkości ścinania ścianki.

Zobacz też

• Krytyczne rozwiązane naprężenia ścinające
• Bezpośredni test ścinania
• Tarcie
• Diagramy ścinania i momentów
• Szybkość ścinania
• Odkształcenie ścinające
• Wytrzymałość na ścinanie
• Naprężenie rozciągające
• Próba ścinania trójosiowego