Binarna grupa czworościenna

Regularny złożony wielotop , 3{6}2 lub lub , reprezentuje diagram Cayleya dla binarnej grupy tetraedrycznej, gdzie każdy czerwony i niebieski trójkąt jest skierowanym podwykresem.

W matematyce binarna grupa tetraedryczna , oznaczona jako 2T lub ⟨2,3,3⟩, jest pewną nieabelową grupą rzędu 24. Jest przedłużeniem grupy tetraedrycznej T lub (2,3,3) rzędu 12 o grupa cykliczna rzędu 2 i jest preobrazem grupy czworościennej pod homomorfizmem obejmującym 2: 1 Spin(3) → SO(3) specjalnej grupy ortogonalnej przez grupę spinową . Wynika z tego, że binarna grupa czworościenna jest dyskretną podgrupą Spinu (3) rzędu 24. Złożona grupa refleksyjna nazwana 3 (24) 3 przez GC Shepharda lub 3 [3] 3 i Coxetera jest izomorficzna z binarną grupą czworościenną .

Binarną grupę czworościenną najłatwiej opisać konkretnie jako dyskretną podgrupę kwaternionów jednostkowych , pod izomorfizmem Spin (3) ≅ Sp (1) , gdzie Sp (1) jest multiplikatywną grupą kwaternionów jednostkowych. (Opis tego homomorfizmu znajduje się w artykule na temat kwaternionów i obrotów przestrzennych ).

Elementy

Wykres Cayleya SL(2,3)

Projekcje symetrii

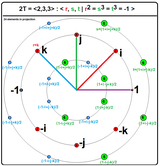8-krotny	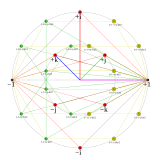12-krotny
24 elementy kwaternionów: 1 zamówienie-1:1 1 zamówienie-2: -1 6 rząd-4: ±i, ±j, ±k 8 rząd-6: (+1±i±j±k)/2 8 rząd-3: (-1±i±j±k)/2.

Wyraźnie, binarna grupa czworościenna jest podana jako grupa jednostek w pierścieniu liczb całkowitych Hurwitza . Istnieje 24 takich jednostek podanych przez

${\ Displaystyle \ {\ pm 1, \ pm ja, \ pm j, \ pm k, {\ tfrac {1}{2}}(\pm 1\pm i\pm j\pm k)\}}$

ze wszystkimi możliwymi kombinacjami znaków.

Wszystkie 24 jednostki mają wartość bezwzględną 1 i dlatego należą do grupy kwaternionów jednostek Sp(1). Wypukły kadłub tych 24 elementów w 4-wymiarowej przestrzeni tworzy wypukły regularny 4-polytop zwany 24-komorowym .

Nieruchomości

Binarna grupa tetraedryczna, oznaczona przez 2T, pasuje do krótkiego ciągu dokładnego

${\ Displaystyle 1 \ do \ {\ pm 1 \} \ do 2 \ operatorname {T} \ do \ operatorname {T} \ do 1.}$

Ta sekwencja się nie rozdziela , co oznacza, że ​​2T nie jest półprostym iloczynem {±1} przez T. W rzeczywistości nie ma podgrupy 2T izomorficznej z T.

Binarna grupa czworościenna jest grupą pokrywającą grupę czworościenną. Myśląc o grupie czworościennej jako grupie naprzemiennej na czterech literach, T ≅ ZA ₄ , mamy zatem binarną grupę czworościenną jako grupę pokrywającą, 2T ≅ ${\ Displaystyle {\ widehat {\ operatorname {A} _ {4 }}}}$ .

Centrum 2T to podgrupa {±1} . Wewnętrzna grupa automorfizmów jest izomorficzna z A ₄ , a pełna grupa automorfizmów jest izomorficzna z S ₄ .

Mnożenie w lewo przez − ω , element rzędu -6: spójrz na szare, niebieskie, fioletowe i pomarańczowe kule i strzałki, które tworzą 4 orbity (dwie strzałki nie są pokazane). samo ω jest kulą znajdującą się najniżej: ω = (− ω )(−1) = (− ω ) ⁴

Binarną grupę czworościenną można zapisać jako iloczyn półprosty

${\ Displaystyle 2 \ operatorname {T} = \ operatorname {Q} \ rtimes \ operatorname {C} _ {3}}$

gdzie Q jest grupą kwaternionów składającą się z 8 jednostek Lipschitza , a C ₃ jest grupą cykliczną rzędu 3 generowaną przez ω = − 1 / 2 (1 + i + j + k ) . Grupa Z ₃ oddziałuje na normalną podgrupę Q przez koniugację . Koniugacja przez ω jest automorfizmem Q, który cyklicznie obraca i , j i k .

Można pokazać, że binarna grupa tetraedryczna jest izomorficzna ze specjalną grupą liniową SL(2,3) – grupą wszystkich macierzy 2 × 2 nad ciałem skończonym F ₃ z wyznacznikami jednostkowymi, przy czym izomorfizm ten obejmuje izomorfizm rzutowej specjalnej grupa liniowa PSL(2,3) z grupą naprzemienną A ₄ .

Prezentacja

Grupa 2T ma prezentację wygłoszoną przez

${\ Displaystyle \ langle r, s, t \ środkowy r ^ {2} = s ^ {3} = t ^ {3} = pierwszy\szereg }$

lub równoważnie,

${\ Displaystyle \ langle s, t \ mid (st) ^ {2} = s ^ {3} = t ^ {3} \ rangle.}$

Generatory z tymi relacjami są podane przez

${\ Displaystyle r = i \ qquad s = {\ tfrac {1} {2}} (1+i+j+k)\qquad t={\tfrac {1}{2}}(1+i+jk),}$

z ${\ Displaystyle r ^ {2} = s ^ {3} = t ^ {3} = -1}$ .

Podgrupy

Binarna grupa tetraedryczna 2T=<3,3,2> ma 2 podstawowe podgrupy: • Grupa kwaternionów , Q=<2,2,2>, indeks 3 • Grupa cykliczna Z6=<3>, indeks 4.

Grupa kwaternionów składająca się z 8 jednostek Lipschitza tworzy normalną podgrupę 2T o indeksie 3. Ta grupa i centrum {±1} są jedynymi nietrywialnymi podgrupami normalnymi.

Wszystkie inne podgrupy 2T to grupy cykliczne generowane przez różne elementy, z rzędami 3, 4 i 6.

Wyższe wymiary

Tak jak grupa tetraedryczna uogólnia się na grupę symetrii obrotowej n - simpleksu (jako podgrupę SO( n )), istnieje odpowiadająca jej wyższa grupa binarna, która jest 2-krotnym pokryciem, pochodzącym z pokrycia Spin( n ) → SO( n ).

Grupę symetrii obrotowej n -simpleksu można uznać za grupę naprzemienną w punktach n + 1, An _{+ 1} , a odpowiadająca jej grupa binarna jest 2-krotną grupą pokrywającą . Dla wszystkich wyższych wymiarów z wyjątkiem A ₆ i A ₇ (odpowiadających 5-wymiarowym i 6-wymiarowym simpleksom), ta grupa binarna jest grupą pokrywającą (maksymalne pokrycie) i jest superdoskonała , ale dla wymiaru 5 i 6 istnieje dodatkowy wyjątkowy 3-krotne pokrycie, a grupy binarne nie są superdoskonałe.

Zastosowanie w fizyce teoretycznej

Binarna grupa czworościenna została użyta w kontekście teorii Yanga-Millsa w 1956 roku przez Chen Ning Yang i innych. Po raz pierwszy został użyty w budowaniu modelu fizyki smaku przez Paula Framptona i Thomasa Kepharta w 1994 roku. W 2012 roku wykazano, że zależność między dwoma kątami mieszania neutrin, wyznaczona przy użyciu tej binarnej czworościennej symetrii smaku, jest zgodna z eksperymentem.

Zobacz też

• Binarna grupa wielościenna
• Binarna grupa cykliczna , ⟨ n ⟩, rząd 2 n
• Binarna grupa dwuścienna , ⟨2,2, n ⟩, rząd 4 n
• Binarna grupa oktaedryczna , 2O = ⟨2,3,4⟩, rząd 48
• Binarna grupa dwudziestościenna , 2I = ⟨2,3,5⟩, rząd 120

Notatki

•   Conway, John H .; Smith, Derek A. (2003). O kwaternionach i oktonionach . Natick, Massachusetts: AK Peters, Ltd. ISBN 1-56881-134-9 .
•   Coxeter, HSM & Moser, WOJ (1980). Generatory i relacje dla grup dyskretnych, wydanie 4 . Nowy Jork: Springer-Verlag. ISBN 0-387-09212-9 . 6.5 Binarne grupy wielościenne, s. 68