Kwaterniony i rotacja przestrzenna

Kwaterniony jednostkowe , zwane wersorami , zapewniają wygodną notację matematyczną do przedstawiania orientacji przestrzennych i obrotów elementów w przestrzeni trójwymiarowej. W szczególności kodują informacje o obrocie kąta osi wokół dowolnej osi. Kwaterniony rotacyjne i orientacyjne mają zastosowanie w grafice komputerowej , wizji komputerowej , robotyce , nawigacji , dynamice molekularnej , dynamika lotu , mechanika orbitalna satelitów i analiza tekstur krystalograficznych .

Kiedy są używane do reprezentowania rotacji, kwaterniony jednostkowe są również nazywane kwaternionami rotacyjnymi , ponieważ reprezentują grupę rotacyjną 3D . Kiedy są używane do przedstawienia orientacji (obrót względem układu współrzędnych odniesienia), nazywane są kwaternionami orientacji lub kwaternionami położenia . Obrót przestrzenny wokół stałego punktu $wokół$ osi jednostkowej ${\ displaystyle (X, Y, Z)}$ oznacza $_$ Eulera kwaternion = ${\ Displaystyle C = \ cos (\ teta / 2)}$ i ${\ Displaystyle S = \ grzech (\ teta / 2)}$ .

W porównaniu do macierzy rotacyjnych kwaterniony są bardziej zwarte, wydajne i numerycznie stabilne . W porównaniu do kątów Eulera są one prostsze do skomponowania . Nie są one jednak tak intuicyjne i łatwe do zrozumienia i ze względu na okresowy charakter sinusa ${\ displaystyle [0,2 \ pi]}$ cosinusa kąty obrotu różniące się dokładnie okresem naturalnym zostaną zakodowane w identycznych kwaternionach, a odzyskane kąty w radianach zostaną ograniczone do [ .

Używanie kwaternionów jako rotacji

$o$ 3D kuli i obrót wokół osi Eulera ( kąt ${\ displaystyle \ theta}$

  W przestrzeni trójwymiarowej, zgodnie z twierdzeniem Eulera o rotacji , dowolny obrót lub sekwencja obrotów ciała sztywnego lub układu współrzędnych wokół stałego punktu jest równoważna pojedynczemu obrotowi o dany kąt wokół ustalonej osi ${\ displaystyle \ theta}$ (zwaną osią Eulera ), która przebiega przez stały punkt. Oś Eulera jest zwykle reprezentowana przez $}$ jednostkowy $}$ \ displaystyle {\ kapelusz {e}   na obrazie). $dowolny obrót w$ trzech wymiarach można przedstawić $.$ wektora i skalara

Kwaterniony umożliwiają prosty sposób zakodowania reprezentacji kąta osi w czterech liczbach i można ich użyć do zastosowania (obliczenia) odpowiedniego obrotu do wektora położenia (x,y,z) , reprezentującego punkt względem początku w R ³ .

Wektory euklidesowe takie jak (2, 3, 4) lub ( a _x , a _y , a _z ) można zapisać jako 2 i + 3 j + 4 k lub     a _x i + a _y j + a _z k , gdzie i , j , k to wektory jednostkowe reprezentujące trzy osie kartezjańskie (tradycyjnie x , y , z ), a także przestrzegać zasad mnożenia podstawowych jednostek kwaternionów.

Dlatego obrót kąta $osi$ określonej przez wektor jednostkowy

${\ Displaystyle {\ vec {u}} = (u_ {x}, u_ {y}, u_ {z })=u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} }$

można przedstawić za pomocą kwaternionu. Można to zrobić za pomocą rozszerzenia wzoru Eulera :

${\ Displaystyle \ mathbf {q} = e ^ {{\ Frac {\ theta} {2}} (u_ {x} \ mathbf {i} + u_ {y} \ mathbf {j} + u_ {z} \ mathbf {k} )}}=\cos {\frac {\theta }{2}}+(u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf { k} )\sin {\frac {\theta} {2}}}$

Można wykazać , że żądany obrót można zastosować do zwykłego wektora. ${\ displaystyle \ mathbf { p} =(p_{x},p_{y},p_{z})=p_{x}\mathbf {i} +p_{y}\mathbf {j} +p_{z}\mathbf {k} }$ w przestrzeni trójwymiarowej, traktowanej jako kwaternion o rzeczywistej współrzędnej równej zero, poprzez ocenę koniugacji p przez q :

${\ Displaystyle \ mathbf {p '} = \ mathbf {q} \ mathbf {p} \ mathbf {q} ^ {-1}}$

korzystając z iloczynu Hamiltona , gdzie p ′ = ( p _x ′, p _y ′, p _z ′) jest nowym wektorem położenia punktu po obrocie. W implementacji programowej koniugację osiąga się poprzez skonstruowanie kwaternionu, którego część wektorowa wynosi p , a część rzeczywista równa zero, a następnie wykonując mnożenie kwaternionów. Część wektorowa powstałego kwaternionu jest pożądanym wektorem p ′ .

Faktem geometrycznym niezależnym od kwaternionów jest istnienie odwzorowania dwa do jednego z rotacji fizycznych na macierze transformacji rotacyjnej. Jeśli , $displaystyle {$ obrót o $vec {u}}}$$\$ przez $displaystyle \ teta}$ i fizyczny obrót o ${\ Displaystyle - {\ vec {u}}}$ o ${\ Displaystyle 2 \ pi - \ theta}$ oba osiągają tę samą końcową orientację poprzez rozłączne ścieżki poprzez orientacje pośrednie. Wstawiając te wektory i kąty do powyższego wzoru na q , okazuje się, że jeśli q oznacza pierwszy obrót, - q oznacza drugi obrót. Jest to geometryczny dowód, że koniugacja przez q i przez - q musi dać tę samą macierz transformacji rotacyjnej. Fakt ten potwierdza się algebraicznie zauważając, że koniugacja jest kwadratowa w q , więc znak q anuluje i nie ma wpływu na wynik. (Patrz mapowanie 2: 1 SU (2) na SO (3) ) Jeśli oba obroty są o pół obrotu, zarówno q , jak i - q będą miały ${\ displaystyle (\ theta = \ pi)}$ rzeczywista współrzędna równa zeru. W przeciwnym razie jedna będzie miała dodatnią część rzeczywistą, reprezentującą obrót o kąt mniejszy niż , $displaystyle$ druga będzie miała ujemną część rzeczywistą, reprezentującą obrót o kąt większy niż $\ pi} }$ .

Matematycznie operacja ta przenosi do siebie zbiór wszystkich „czystych” kwaternionów p (tych, których część rzeczywista jest równa zeru) – które tworzą trójwymiarową przestrzeń pomiędzy kwaternionami – w sobie, poprzez pożądany obrót wokół osi u , o kąt θ. (W wyniku tej operacji każdy prawdziwy kwaternion jest przenoszony w siebie. Jednak na potrzeby obrotów w przestrzeni trójwymiarowej ignorujemy rzeczywiste kwaterniony.)

$skierowana$ w tym samym kierunku, .

W tym przypadku q jest kwaternionem jednostkowym i

${\ Displaystyle \ mathbf {q} ^ {-1} = e ^ {- {\ Frac {\ theta} {2}} (u_ {x} \ mathbf {i} + u_ {y} \ mathbf {j} +u_{z}\mathbf {k} )}}=\cos {\frac {\theta }}-(u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_ {z}\mathbf {k})\sin {\frac {\theta}}.}$

Wynika z tego, że koniugacja przez iloczyn dwóch kwaternionów jest złożeniem koniugacji przez te kwaterniony: Jeśli p i q są kwaternionami jednostkowymi, to rotacja (sprzężenie) o pq wynosi

${\ Displaystyle \ mathbf {pq} {\ vec {v}} ( \mathbf {pq} )^{-1}=\mathbf {pq} {\vec {v}}\mathbf {q} ^{-1}\mathbf {p} ^{-1}=\mathbf {p} (\mathbf {q} {\vec {v}}\mathbf {q} ^{-1})\mathbf {p} ^{-1}}$ ,

co jest równoznaczne z obracaniem (sprzęganiem) o q , a następnie o p . Składnik skalarny wyniku musi koniecznie wynosić zero.

Kwaternion odwrotny do rotacji jest przeciwną rotacją, ponieważ ${\ displaystyle \ mathbf {q} ^ {-1} (\ mathbf {q} {\ vec { v}}\mathbf {q} ^{-1})\mathbf {q} ={\vec {v}}}$ . Kwadrat obrotu kwaternionu to obrót o dwukrotność kąta wokół tej samej osi. Mówiąc bardziej ogólnie, q ⁿ jest obrotem o n razy kąt wokół tej samej osi co q . Można to rozszerzyć na dowolną wartość rzeczywistą n , pozwalający na płynną interpolację pomiędzy orientacjami przestrzennymi; zobacz Slerp .

Dwa kwaterniony rotacyjne można połączyć w jeden równoważny kwaternion według zależności:

${\ Displaystyle \ mathbf {q} '= \ mathbf {q} _ {2} \ mathbf {q} _ {1}}$

gdzie q ′ odpowiada obrotowi q ₁ , po którym następuje obrót q ₂ . W ten sposób można złożyć dowolną liczbę obrotów, a następnie zastosować je jako pojedynczy obrót. (Zauważ, że mnożenie kwaternionów nie jest przemienne .)

Przykładowa operacja koniugacji

Obrót o 120° wokół pierwszej przekątnej zmienia i , j i k cyklicznie

Koniugacja p przez q odnosi się do operacji p ↦ qpq ⁻¹ .

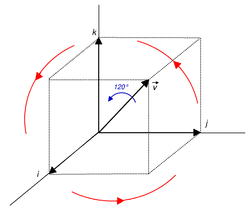
  Rozważ obrót f wokół osi , przy kącie obrotu wynoszącym ${\ displaystyle {\ vec {v}} = \ mathbf {i} + \ mathbf {j} + \ mathbf {k}}$ 120°, czyli 2 π / 3 radiany .

${\ Displaystyle \ alfa = {\ Frac {2 \ pi} {3}}}$

p ↦ q p dla q = 1 + i + jot + k / 2 na jednostce 3-sfera . Zauważ, że to jednostronne (mianowicie lewe ) mnożenie daje obrót kwaternionów o 60°

Długość $→ {\ displaystyle {\ vec {$ √ 3 , półkąt π / 3 (60°) z cosinusem √ } } 1/2 ( } 3/2 cos 60° = 0,5 ) i sinusem v , ( grzech 60° ≈ 0,866 ). Mamy zatem do czynienia z koniugacją przez kwaternion jednostkowy

${\ Displaystyle {\ początek {wyrównane} u & = \ cos {\ Frac {\ alfa} {2}} + \ grzech {\ Frac {\ alfa} {2 }}\cdot {\frac {1}{\|{\vec {v}}\|}}{\vec {v}}\\&=\cos {\frac {\pi }{3}}+\ grzech {\frac {\pi }{3}}\cdot {\frac {1}{\sqrt {3}}}{\vec {v}}\\&={\frac {1}{2}}+ {\frac {\sqrt {3}}}} } + {\ Frac {\sqrt {3}}}} &={\frac {1+\mathbf {i} +\mathbf {j} +\mathbf {k} }{2}}\end{aligned}}}$

Jeśli f jest funkcją rotacji,

${\ Displaystyle f (a \ mathbf {i} + b \ mathbf {j} + c \ mathbf {k } )=u(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} )u^{-1}}$

Można udowodnić, że odwrotność kwaternionu jednostkowego uzyskuje się po prostu zmieniając znak jego urojonych składników. W konsekwencji,

${\ Displaystyle u ^ {- 1} = {\ dfrac {1- \ mathbf {i} - \ mathbf {j} - \ mathbf {k}} {2}} }$

I

${\ Displaystyle f (a \ mathbf {i} + b \ mathbf {j} + c \ mathbf {k}) = {\ dfrac {1 + \ mathbf {i} + \ mathbf {j} + \ mathbf {k} } } }{2}}}$

Można to uprościć, stosując zwykłe zasady arytmetyki kwaternionów

${\ Displaystyle f (a \ mathbf {i} + b \ mathbf {j} + c \ mathbf {k}) = c$

Zgodnie z oczekiwaniami, obrót odpowiada utrzymaniu sześcianu nieruchomego w jednym punkcie i obróceniu go o 120° wokół długiej przekątnej przechodzącej przez stały punkt (zaobserwuj, jak trzy osie są cyklicznie permutowane ).

Macierz rotacji pochodząca z kwaternionów

Rotacja kwaternionów ${\ Displaystyle \ mathbf {p'} = \ mathbf {q} \ mathbf {p} \ mathbf {q} ^ {- 1}} ($ z ${\ Displaystyle \ mathbf {q} = q_ {r} + q_ {i} \ mathbf {i} + q_ {j} \ mathbf {j} + q_ {k} \ mathbf {k} }$ ) można algebraicznie przekształcić w obrót macierzy gdzie jest macierzą rotacji wyrażoną wzorem: $\ displaystyle \$$mathbf {p'} = \ mathbf {Rp}}$

${\ Displaystyle \ mathbf {R} = {\ początek {bmatrix} 1-2s (q_ {j} ^ {2} + q_ {k} ^ {2 })&2s(q_{i}q_{j}-q_{k}q_{r})&2s(q_{i}q_{k}+q_{j}q_{r})\\2s(q_{i} q_{j}+q_{k}q_{r})&1-2s(q_{i}^{2}+q_{k}^{2})&2s(q_{j}q_{k}-q_{i }q_{r})\\2s(q_{i}q_{k}-q_{j}q_{r})&2s(q_{j}q_{k}+q_{i}q_{r})&1- 2s(q_{i}^{2}+q_{j}^{2})\end{bmacierz}}}$

Tutaj i jeśli q $}$ jednostkowym, ${\ Displaystyle s = \ | q \$ .

$wyrażymy$ uzyskać za pomocą rachunku wektorowego i algebry liniowej $,$ jeśli wyrazimy i jako części skalarne i wektorowe oraz wzór na operację mnożenia w równanie ${\ Displaystyle \ mathbf {p'} = \ mathbf {q} \ mathbf {p} \ mathbf {q} ^ {-1}}$ . Jeśli napiszemy jako ${\ displaystyle \ mathbf {p}}$${\ Displaystyle \ lewo (0, \ \ mathbf {p} \ prawo)}$ , ${\ Displaystyle \ mathbf {p} '}$ jako ${\ Displaystyle \ lewo (0, \ \ mathbf {p} '\ prawo)}$ i ${\ displaystyle \ mathbf {q}}$ jak ${\ displaystyle \ lewo (q_ {r}, \ \ mathbf {v} \ prawo)$ } ${\ Displaystyle \ mathbf {v} = \ lewo (q_ {i}, q_ {j}, q_ {k} \ prawo)},$ nasze równanie zamienia się w ${\ Displaystyle \ lewo (0, \ \ mathbf {p} '\ prawo) = \ lewo (q_ {r}, \ \ mathbf {v} \ prawo) \ lewo (0,\ \mathbf {p} \right)s\left(q_{r},\ -\mathbf {v} \right)}$ . Korzystając ze wzoru na mnożenie dwóch kwaternionów wyrażonych jako części skalarne i wektorowe,

${\ Displaystyle \ lewo (r_ {1}, \ {\ vec {v}} _ {1} \ prawo) \ lewo (r_ {2}, \ {\ vec {v}} _ {2} \ prawo) = \left(r_{1}r_{2}-{\vec {v}}_{1}\cdot {\vec {v}}_{2},\ r_{1}{\vec {v}}_ {2}+r_{2}{\vec {v}}_{1}+{\vec {v}}_{1}\times {\vec {v}}_{2}\right),}$

to równanie można przepisać jako

${\ Displaystyle {\ początek {wyrównane} (0, \ \ mathbf {p} ') = & ((q_ {r}, \ \ mathbf {v}) (0, \ \ mathbf {p})) s (q_ {r},\ -\mathbf {v} )\\=&(q_{r}0-\mathbf {v} \cdot \mathbf {p} ,\ q_{r}\mathbf {p} +0\mathbf {v} +\mathbf {v} \times \mathbf {p} )s(q_{r},\ -\mathbf {v} )\\=&s(-\mathbf {v} \cdot \mathbf {p} ,\ q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )(q_{r},\ -\mathbf {v} )\\=&s(-\mathbf {v} \cdot \mathbf {p} q_{r}-(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )\cdot (-\mathbf {v} ),\ (- \mathbf {v} \cdot \mathbf {p} )(-\mathbf {v} )+q_{r}(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} ) +(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )\times (-\mathbf {v} ))\\=&s\left(-\mathbf {v} \ cdot \mathbf {p} q_{r}+q_{r}\mathbf {v} \cdot \mathbf {p} ,\ \mathbf {v} \left(\mathbf {v} \cdot \mathbf {p} \ prawo)+q_{r}^{2}\mathbf {p} +q_{r}\mathbf {v} \times \mathbf {p} +\mathbf {v} \times \left(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} \right)\right)\\=&\left(0,\ s\left(\mathbf {v} \otimes \mathbf {v} +q_ {r}^{2}\mathbf {I} +2q_{r}[\mathbf {v} ]_{\times }+[\mathbf {v} ]_{\times }^{2}\right)\ mathbf {p} \right),\end{aligned}}}$

gdzie oznacza iloczyn zewnętrzny , $\$$displaystyle \ mathbf {ja}}$ jest macierzą tożsamości i $\ razy}}$ { macierz transformacji, która pomnożona od prawej strony przez wektor daje iloczyn krzyżowy $\ razy \ mathbf {u}}$$mathbf {v$ .

Ponieważ możemy zidentyfikować jako $\ mathbf {R} \ mathbf {p}$${\ displaystyle \ mathbf {p} '=$${\ Displaystyle s \ lewo (\ mathbf {v} \ otimes \ mathbf {v} + q_ {r} ^ {2} \ mathbf {I} +2q_ {r} [\ mathbf {v} ] _ {\ razy} +[\mathbf {v} ]_{\times }^{2}\right)}$ , co po rozwinięciu powinno dać w wyniku wyrażenie zapisane w powyższej postaci macierzowej.

Odzyskiwanie reprezentacji osi i kąta

Wyrażenie obraca dowolny $}$ wektora wokół osi określonej przez ${\ displaystyle \ mathbf {q} \ mathbf {p} \ mathbf {q} ^ {-1}$ wektor ${$ kąt gdzie i zależy od kwaternionu $a$$\$$}$${\ Displaystyle \ mathbf {q} = q_ {r} + q_ {i} \ mathbf {i} + q_ {j} \ mathbf {j} + q_ {k} \ mathbf {k} }$ .

$mathbf {a}}$${\ displaystyle \ mathbf {a}}$ i można znaleźć na podstawie następujących równań: za

${\ Displaystyle {\ rozpocząć {wyrównane} (a_ {x}, a_ {y}, a_ {z}) = {} & {\ Frac {(q_ {i}, q_ {j}, q_ {k})} {\sqrt {q_{i}^{2}+q_{j}^{2}+q_{k}^{2}}}}\\[2pt]\theta =2\nazwa operatora {atan2} &\left ({\sqrt {q_{i}^{2}+q_{j}^{2}+q_{k}^{2}}},\,q_{r}\right),\end{aligned}} }$

gdzie $tangensem$ jest dwuargumentowym arcus .

Należy zachować ostrożność, gdy kwaternion zbliża się do skalara , ponieważ z powodu degeneracji oś rotacji tożsamości nie jest dobrze zdefiniowana.

Skład obrotów przestrzennych

Zaletą sformułowania kwaternionowego składu dwóch obrotów R _B i RA jest to, że daje ono bezpośrednio oś obrotu _i kąt złożonego obrotu R _C = R _B R _A .

Niech kwaternion związany z obrotem przestrzennym $R$ zostanie zbudowany z jego osi obrotu S z kątem obrotu tej osi. Powiązany kwaternion jest podany przez

$${\ Displaystyle S = \ cos {\ Frac {\ Varphi} {2}} + \ mathbf {S} \ sin {\ Frac {\ Varphi} {2}}.}$$

Wtedy złożenie obrotu R _B z RA jest obrotem R _C = R _B R _{A z osią obrotu i kątem określonym} przez iloczyn kwaternionów

$${\ Displaystyle A = \ cos {\ Frac {\ alfa} {2}} + \ mathbf {A} \sin {\frac {\alfa }}\quad {\text{i}}\quad B=\cos {\frac {\beta }}+\mathbf {B} \sin {\frac {\beta} {2}},}$$

to jest

$${\ Displaystyle C = \ cos {\ frac {\ gamma} {2}} + \ mathbf {C} \ sin {\ frac {\ gamma} {2}} = \ lewo (\ cos {\ frac {\ beta} {2}}+\mathbf {B} \sin {\frac {\beta }}\right)\left(\cos {\frac {\alfa }}+\mathbf {A} \sin {\frac {\alfa} {2}}\dobrze).}$$

Rozwiń ten produkt, aby uzyskać

$${\ Displaystyle \ cos {\ Frac {\ gamma} {2}} + \ mathbf {C} \ grzech {\ Frac {\ gamma} {2}} = \ lewo (\ cos {\ frac {\ beta} {2 }} \ cos {\ frac {\ alfa } } - \ mathbf {B} \ cdot \ mathbf {A} \ sin {\ frac {\ beta } } \ sin {\ frac {\ alfa } {2}}\right)+\left(\mathbf {B} \sin {\frac {\beta }{2}}\cos {\frac {\alfa }{2}}+\mathbf {A} \sin {\ Frac {\alpha }} \sin {\frac {\alfa} {2}}\right).}$$

Podziel obie strony tego równania przez tożsamość, czyli prawo cosinusów na kuli ,

$${\ Displaystyle \ cos {\ Frac {\ gamma} {2}} = \ cos {\ Frac {\ beta }{2}}\cos {\frac {\alpha }}-\mathbf {B} \cdot \mathbf {A} \sin {\frac {\beta }}\sin {\frac {\alfa} {2}},}$$

i obliczyć

$${\ Displaystyle \ mathbf {C} \ tan {\ Frac {\ gamma} {2}} = {\ Frac {\ mathbf {B} \ tan {\ Frac {\ beta} {2}} + \ mathbf {A} \tan {\frac {\alfa }}+\mathbf {B} \times \mathbf {A} \tan {\frac {\beta }}\tan {\frac {\alfa} {2 }}}}$$

Jest to wzór Rodriguesa na oś złożonego obrotu określoną w kategoriach osi dwóch obrotów. Wyprowadził tę formułę w 1840 r. (patrz strona 408).

Trzy osie obrotu A , B i C tworzą trójkąt sferyczny, a kąty dwuścienne pomiędzy płaszczyznami utworzonymi przez boki tego trójkąta są określone przez kąty obrotu. Hamilton przedstawił składową postać tych równań, pokazując, że iloczyn kwaternionów oblicza trzeci wierzchołek trójkąta sferycznego na podstawie dwóch danych wierzchołków i powiązanych z nimi długości łuków, co definiuje również algebrę punktów w geometrii eliptycznej .

Kompozycja osiowo-kątowa

Znormalizowana oś obrotu, usuwająca $. Należy$ wektor będący osią obrotu razy $}$ ostrożność $normalizując$ wektor osi, gdy jest blisko ; γ { $gamma$$\$ co jest tożsamością lub 0 obrotem wokół dowolnej osi.

$${\ Displaystyle {\ początek {wyrównane} \ gamma i = 2 \ cos ^ {-1} \ lewo (\ cos {\ Frac {\ beta} {2}} \ cos { \frac {\alpha }}-\mathbf {B} \cdot \mathbf {A} \sin {\frac {\beta }}\sin {\frac {\alfa }}}\ prawo)\\\mathbf {D} &=\mathbf {B} \sin {\frac {\beta }{2}}\cos {\frac {\alfa }{2}}+\mathbf {A} \sin {\ Frac {\alpha }} \sin {\frac {\alfa }{2}}\end{aligned}}}$$

Lub z podstawieniami trygonometrycznymi z dodawaniem kątów ...

$${\ Displaystyle {\ początek {wyrównane} \ gamma i = 2 \ cos ^ {- 1} \ lewo (\ lewo (1- \ mathbf {A} \ cdot \ mathbf {B} \ prawo) \ cos {\ frac { \beta -\alpha }{2}}+\left(1+\mathbf {A} \cdot \mathbf {B} \right)\cos {\frac {\beta +\alpha }{2}}\right) \\\mathbf {D} &=\left(\sin {\frac {\beta +\alpha }{2}}+\sin {\frac {\beta -\alpha }{2}}\right)\mathbf {A} +\left(\sin {\frac {\beta +\alfa }{2}}-\sin {\frac {\beta -\alpha }}\right)\mathbf {B} +\ lewy (\cos {\frac {\beta -\alfa }-\cos {\frac {\beta +\alfa } {2}}\prawy)\mathbf {B} \times \mathbf {A} \end{aligned}}}$$

ostatecznie normalizowanie osi obrotu: ${\textstyle {\frac {\mathbf {D}}}$ lub $mathbf {D}} {\|\mathbf {D} \|}}}$ \

Różniczkowanie ze względu na kwaternion rotacji

Obrócony kwaternion p' = q p q ⁻¹ należy różniczkować względem obracającego się kwaternionu q , gdy rotacja jest szacowana na podstawie optymalizacji numerycznej. Oszacowanie kąta obrotu jest niezbędną procedurą podczas rejestracji obiektów 3D lub kalibracji kamery. Dla unitarnego q i czystego urojonego p , czyli dla rotacji w przestrzeni 3D, pochodne obróconego kwaternionu można przedstawić za pomocą zapisu rachunku macierzowego jako

${\ Displaystyle {\ początek {wyrównane} {\ Frac {\ częściowe \ mathbf {p '}} {\częściowe q_{0}}},{\frac {\częściowe \mathbf {p'} }{\częściowe q_{x}}},{\frac {\częściowe \mathbf {p'} }{\częściowe q_ {y}}}, {\frac {\częściowe \mathbf {p'} } }częściowe q_{z}}}\right]=\left[\mathbf {pq} -(\mathbf {pq})^{ *},(\mathbf {pqi} )^{*}-\mathbf {pqi} ,(\mathbf {pqj} )^{*}-\mathbf {pqj} ,(\mathbf {pqk} )^{*} -\mathbf {pqk} \right].\end{aligned}}}$

Wyprowadzenie można znaleźć w.

Tło

Kwaterniony

Główny artykuł: kwaterniony

Liczby zespolone można zdefiniować wprowadzając abstrakcyjny symbol i , który spełnia zwykłe zasady algebry i dodatkowo regułę i ² = −1 . To wystarczy, aby odtworzyć wszystkie zasady arytmetyki liczb zespolonych: na przykład:

${\ Displaystyle (a + b \ mathbf {i}) (c + d \ mathbf {i}) = ac + reklama \ mathbf {i} + b \ mathbf {i} c + b \ mathbf {i} d \ mathbf {i} =ac+ad\mathbf {i} +bc\mathbf {i} +bd\mathbf {i} ^{2}=(ac-bd)+(bc+ad)\mathbf {i} .}$

W ten sam sposób kwaterniony można zdefiniować wprowadzając abstrakcyjne symbole i , j , k spełniające reguły i ² = j ² = k ² = i j k = −1 i zwykłe reguły algebraiczne z wyjątkiem przemiennego prawa mnożenia (znany przykład takiego nieprzemiennego mnożenia jest mnożeniem macierzy ). Z tego wynikają wszystkie zasady arytmetyki kwaternionów, takie jak zasady mnożenia elementów bazowych kwaternionów . Korzystając z tych reguł, można wykazać, że:

${\ Displaystyle {\ początek {wyrównane} i (a + b \ mathbf {i} + c \ mathbf {j} + d \ mathbf {k}) (e + f \ mathbf {i} + g \ mathbf {j} +h\mathbf {k} )=\\&(ae-bf-cg-dh)+(af+be+ch-dg)\mathbf {i} +(ag-bh+ce+df)\mathbf {j } +(ah+bg-cf+de)\mathbf {k} .\end{aligned}}}$

Część urojona kwaternionu zachowuje się jak wektor ${\ Displaystyle {\ vec {v}} = (b, c, d)}$${\ displaystyle b\ mathbf {i} + c \ mathbf {j} +d \ mathbf {$ w trójwymiarowej przestrzeni wektorowej , a część rzeczywista a zachowuje się jak skalar w R . Kiedy w geometrii używane są kwaterniony, wygodniej jest zdefiniować je jako skalar plus wektor :

${\ Displaystyle a + b \ mathbf {i} + c \ mathbf {j} + d \ mathbf {k} = a + {\ vec {v}}.}$

Niektórym może wydawać się dziwne dodawanie liczby do wektora , ponieważ są to obiekty o bardzo różnej naturze, lub mnożenie dwóch wektorów przez siebie, ponieważ operacja ta jest zwykle nieokreślona. Jeśli jednak pamięta się, że jest to zwykły zapis rzeczywistych i urojonych części kwaternionu, staje się to bardziej uzasadnione. Innymi słowy, prawidłowym rozumowaniem jest dodanie dwóch kwaternionów, jednego z zerowym wektorem/częścią urojoną, a drugiego z zerową częścią skalarną/rzeczywistą:

${\ Displaystyle q_ {1} = s + {\ vec {v}} = \ lewo (s, {\ vec {0}} \ prawo) + \ lewo (0, {\ vec {v}} \ prawo).}$

Możemy wyrazić mnożenie kwaternionów we współczesnym języku wektorowych iloczynów krzyżowych i kropkowych (które w rzeczywistości były inspirowane przede wszystkim kwaternionami). Przy mnożeniu części wektorowych/urojonych zamiast zasad i ² = j ² = k ² = ijk = −1 mamy zasadę mnożenia kwaternionów:

${\ Displaystyle {\ vec {v}} {\ vec {w}} = - {\ vec {v}} \ cdot {\ vec { w}}+{\vec {v}}\times {\vec {w}},}$

Gdzie:

• ${\ Displaystyle {\ vec {v}} {\ vec {w}}}$ jest wynikowym kwaternionem,
• ${\ Displaystyle {\ vec {v}} \ razy {\ vec {w}}}$ jest iloczynem wektorowym (wektorem),
• ${\ displaystyle {\ vec {v}} \ cdot {\ vec {w}}}$ jest wektorowym iloczynem skalarnym (skalarem).

Mnożenie kwaternionów jest nieprzemienne (ze względu na iloczyn krzyżowy, który przeciwdziała dojazdom ), podczas gdy mnożenia skalarno-skalarne i skalarno-wektorowe dojeżdżają do pracy. Z tych zasad wynika od razu, że ( patrz szczegóły ):

${\ Displaystyle q_ {1} q_ {2} = \ lewo (s + {\ vec {v}} \ prawo) \ lewo (t + {\ vec {w}} \ prawo) = \ lewo (st- {\ vec { v}}\cdot {\vec {w}}\right)+\left(s{\vec {w}}+t{\vec {v}}+{\vec {v}}\times {\vec { w}}\prawo).}$

(lewa i prawa) multiplikatywna odwrotność lub odwrotność niezerowego kwaternionu jest określona przez stosunek koniugatu do normy ( zobacz szczegóły ):

${\ Displaystyle q_ {1} ^ {-1} = \ lewo (s + {\ vec {v}} \ prawo) ^ {-1} = {\ Frac {\ lewo (s + {\ vec {v}} \ prawo )^{*}}{\lPion s+{\vec {v}}\rPion ^{2}}}={\frac {s-{\vec {v}}}{s^{2}+\lPionek { \vec {v}}\rVert ^{2}}},}$

co można sprawdzić za pomocą bezpośrednich obliczeń (zwróć uwagę na podobieństwo do multiplikatywnej odwrotności liczb zespolonych ).

Tożsamość rotacyjna

Główny artykuł: Wzór na rotację Rodriguesa

Niech będzie wektorem jednostkowym (oś obrotu) i niech $q$$alfa }{2}}+{\vec {u}}\sin {\frac {\alfa }{2}}}$$\ displaystyle q = \ cos {\ frac$ . Naszym celem jest to pokazać

${\ Displaystyle {\ vec {v}} '= q {\ vec {v}} q ^ {-1} = \ lewo (\ cos {\ Frac {\ alfa} {2}} + {\ vec {u} }\sin {\frac {\alfa }}\right)\,{\vec {v}}\,\left(\cos {\frac {\alfa }}-{\vec {u }} \ grzech {\ frac {\ alfa } {2}} \ prawo)}$

$}$ wektor obrócony o kąt wokół osi $}$ \ $displaystyle {\ vec$ Rozszerzanie się (i pamiętanie, że ${\ Displaystyle {\ vec {u}} {\ vec {v}} = {\ vec {u}} \ razy {\vec {v}}-{\vec {u}}\cdot {\vec {v}}} )$ , mamy

${\ Displaystyle {\ początek {wyrównane} {\ vec {v}} '& = {\ vec {v}} \ cos ^ {2} {\ Frac {\ alfa} {2}} + \ lewo ({\ vec {u}} {\vec {v}}-{\vec {v}}{\vec {u}}\right)\sin {\frac {\alfa }}\cos {\frac {\alfa } ={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2\left({\vec {u}}\times {\vec {v}}\right)\ grzech {\ frac {\alfa }}\cos {\frac {\alfa}} -\left(\left({\vec {u}}\times {\vec {v}}\right )-\left({\vec {u}}\cdot {\vec {v}}\right)\right){\vec {u}}\sin ^{2}{\frac {\alpha } }\\[6pt]&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2\left({\vec {u}}\times {\vec { v}}\right)\sin {\frac {\alpha }}\cos {\frac {\alpha }}-\left(\left({\vec {u}}\times {\ vec {v}}\right){\vec {u}}-\left({\vec {u}}\cdot {\vec {v}}\right){\vec {u}}\right)\sin ^^ ({\vec {u}}\times {\vec {v}}\right)\sin {\frac {\alfa }{2}}\cos {\frac {\alfa }}-\left( \left(\left({\vec {u}}\times {\vec {v}}\right)\times {\vec {u}}-\left({\vec {u}}\times {\vec {v}}\right)\cdot {\vec {u}}\right)-\left({\vec {u}}\cdot {\vec {v}}\right){\vec {u}}\ prawo)\sin ^{2}{\frac {\alpha }{2}}\\[6pt]&={\vec {v}}\cos ^{2}{\frac {\alpha }} +2\left({\vec {u}}\times {\vec {v}}\right)\sin {\frac {\alpha }}\cos {\frac {\alpha}} -\left(\left({\vec {v}}-\left({\vec {u}}\cdot {\vec {v}}\right){\vec {u}}\right)-0- \left({\vec {u}}\cdot {\vec {v}}\right){\vec {u}}\right)\sin ^{2}{\frac {\alfa }{2}}\ \[6pt]&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2\left({\vec {u}}\times {\vec {v} }\right)\sin {\frac {\alfa }-2{\vec {u}} \left({\vec {u}}\cdot {\vec {v}}\right)\right)\sin ^{2}{\frac {\alpha }}\\[6pt]&={ \vec {v}}\cos ^{2}{\frac {\alfa }{2}}+2\lewo({\vec {u}}\times {\vec {v}}\right)\sin { \frac {\alfa }}\cos {\frac {\alfa }}-{\vec {v}}\sin ^{2}\frac {\alfa }}+2 {\vec {u}}\left({\vec {u}}\cdot {\vec {v}}\right)\sin ^{2}{\frac {\alpha }{2}}\\[6pt ]&={\vec {v}}\left(\cos ^{2}}{\frac {\alpha }}-\sin ^{2}\frac {\alpha }}\right )+\left({\vec {u}}\times {\vec {v}}\right)\left(2\sin {\frac {\alpha }}\cos {\frac {\alpha} {2}}\right)+{\vec {u}}\left({\vec {u}}\cdot {\vec {v}}\right)\left(2\sin ^{2}{\frac {\alfa }{2}}\right)\\[6pt]\end{aligned}}}$

Używanie tożsamości trygonometrycznych :

${\ Displaystyle {\ początek {wyrównane} {\ vec {v}} '& = {\ vec {v}} \ lewo (\ cos ^ {2} {\ Frac {\ alfa} {2}} - \ sin ^ {2} \alpha } } \right)\left(2\sin ^{2}{\frac {\alpha }{2}}\right)\\[6pt]&={\vec {v}}\cos \alpha +\left({ \vec {u}}\times {\vec {v}}\right)\sin \alpha +{\vec {u}}\left({\vec {u}}\cdot {\vec {v}}\ prawo)\lewo(1-\cos \alpha \right)\\[6pt]&={\vec {v}}\cos \alpha +\left({\vec {u}}\times {\vec {v }}\right)\sin \alpha +{\vec {u}}\left({\vec {u}}\cdot {\vec {v}}\right)-{\vec {u}}\left( {\vec {u}}\cdot {\vec {v}}\right)\cos \alpha \\[6pt]&=\left({\vec {v}}-{\vec {u}}\left ({\vec {u}}\cdot {\vec {v}}\right)\right)\cos \alpha +\left({\vec {u}}\times {\vec {v}}\right) \sin \alpha +{\vec {u}}\left({\vec {u}}\cdot {\vec {v}}\right)\\[6pt]&={\vec {v}}_{ \bot }\cos \alpha +\left({\vec {u}}\times {\vec {v}}\right)\sin \alpha +{\vec {v}}_{\|}\end{ wyrównany}}}$

gdzie ${\ Displaystyle {\ vec {v}} _ {\ bot}}$ i ${\ Displaystyle {\ vec {v}} _ {\ |}}$ są składnikami v → (prostopadłymi i równoległymi do u → odpowiednio). To jest wzór na obrót o oś u → ${\ displaystyle \ alfa}$ .

Operacje rotacyjne kwaternionów

Bardzo formalne wyjaśnienie właściwości użyte w tej sekcji podaje Altman.

Hipersfera obrotów

Główny artykuł: grupa rotacyjna SO (3)

Wizualizacja przestrzeni obrotów

Kwaterniony jednostkowe w bardzo prosty sposób reprezentują grupę obrotów euklidesowych w trzech wymiarach . Zależność między obrotami i kwaternionami można zrozumieć, najpierw wizualizując samą przestrzeń obrotów.

Dwa osobne obroty, różniące się zarówno kątem, jak i osią, w przestrzeni obrotów. Tutaj długość każdego wektora osi jest zależna od odpowiedniej wielkości obrotu wokół tej osi.

Aby zwizualizować przestrzeń obrotów, warto rozważyć prostszy przypadek. Dowolny obrót w trzech wymiarach można opisać obrotem o pewien kąt wokół jakiejś osi ; dla naszych celów użyjemy wektora osi, aby ustalić kierunek naszego kąta. Rozważmy szczególny przypadek, w którym oś obrotu leży w xy . Możemy wówczas określić oś jednego z tych obrotów poprzez punkt na okręgu, przez który przecina się wektor, oraz możemy wybrać promień okręgu, który będzie oznaczał kąt obrotu .

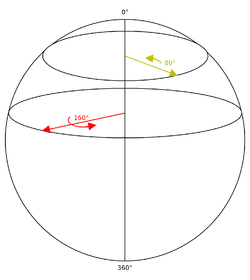
Podobnie obrót, którego oś obrotu leży w płaszczyźnie xy , można opisać jako punkt na kuli o ustalonym promieniu w trzech wymiarach. Zaczynając od bieguna północnego kuli w przestrzeni trójwymiarowej, określamy punkt na biegunie północnym jako obrót tożsamościowy (obrót o kąt zerowy). Podobnie jak w przypadku obrotu tożsamościowego nie jest zdefiniowana oś obrotu, a kąt obrotu (zero) jest nieistotny. Obrót o bardzo małym kącie obrotu można określić poprzez przecięcie kuli równoległej do xy płaszczyźnie i bardzo blisko bieguna północnego. Okrąg wyznaczony przez ten wycinek będzie bardzo mały, co odpowiada małemu kątowi obrotu. Gdy kąty obrotu stają się większe, plasterek przesuwa się w kierunku ujemnego z kierunku, a okręgi stają się większe, aż do osiągnięcia równika kuli, co będzie odpowiadać kątowi obrotu wynoszącemu 180 stopni. Kierując się dalej na południe, promienie okręgów stają się teraz mniejsze (co odpowiada wartości bezwzględnej kąta obrotu uznawanego za liczbę ujemną). Wreszcie, gdy dotrze się do bieguna południowego, okręgi ponownie się kurczą do rotacji tożsamości, która jest również określona jako punkt na biegunie południowym.

Zauważ, że na tej wizualizacji można zobaczyć wiele cech takich obrotów i ich reprezentacji. Przestrzeń obrotów jest ciągła, każdy obrót ma prawie takie same sąsiedztwo obrotów, a otoczenie to staje się płaskie w miarę kurczenia się sąsiedztwa. Ponadto każdy obrót jest w rzeczywistości reprezentowany przez dwa antypodalne punkty na kuli, które znajdują się na przeciwległych końcach linii przechodzącej przez środek kuli. Odzwierciedla to fakt, że każdy obrót można przedstawić jako obrót wokół jakiejś osi lub, równoważnie, jako ujemny obrót wokół osi skierowanej w przeciwnym kierunku (tzw. podwójne pokrycie ). „Szerokość geograficzna” okręgu reprezentującego określony kąt obrotu będzie równa połowie kąta reprezentowanego przez ten obrót, ponieważ w miarę przesuwania się punktu z bieguna północnego na południowy szerokość geograficzna waha się od zera do 180 stopni, podczas gdy kąt obrotu waha się od 0 do 360 stopni. („długość” punktu reprezentuje wówczas określoną oś obrotu). Należy jednak pamiętać, że ten zestaw obrotów nie jest zamknięty w ramach kompozycji. Dwa kolejne obroty z osiami w xy niekoniecznie dadzą obrót, którego oś leży w xy płaszczyźnie, a zatem nie można go przedstawić jako punktu na kuli. Nie będzie tak w przypadku ogólnego obrotu w przestrzeni 3, w którym rotacje tworzą zamknięty zbiór w ramach kompozycji.

Sfera obrotów dla obrotów, które mają oś „poziomą” (w płaszczyźnie xy ).

Wizualizację tę można rozszerzyć na ogólny obrót w przestrzeni trójwymiarowej. Rotacja tożsamości jest punktem, a mały kąt obrotu wokół jakiejś osi można przedstawić jako punkt na kuli o małym promieniu. Wraz ze wzrostem kąta obrotu kula rośnie, aż kąt obrotu osiągnie 180 stopni, w którym to momencie kula zaczyna się kurczyć, stając się punktem, gdy kąt zbliża się do 360 stopni (lub zera stopni od kierunku ujemnego). Ten zbiór rozszerzających się i kurczących sfer reprezentuje hipersferę w przestrzeni czterowymiarowej (3-kula). Podobnie jak w prostszym przykładzie powyżej, każdemu obrotowi reprezentowanemu jako punkt na hipersferze odpowiada jego antypodalny punkt na tej hipersferze. „Szerokość geograficzna” hipersfery będzie równa połowie odpowiedniego kąta obrotu, a sąsiedztwo dowolnego punktu stanie się „bardziej płaskie” (tj. będzie reprezentowane przez trójwymiarową euklidesową przestrzeń punktów), gdy sąsiedztwo się kurczy. Zachowaniu temu odpowiada zbiór kwaternionów jednostkowych: Ogólny kwaternion reprezentuje punkt w przestrzeni czterowymiarowej, ale ograniczenie go do jednostkowej wielkości daje trójwymiarową przestrzeń równoważną powierzchni hipersfery. Wielkość kwaternionu jednostkowego będzie jednością, co odpowiada hipersferze o promieniu jednostkowym. Część wektorowa kwaternionu jednostkowego reprezentuje promień 2-sfery odpowiadający osi obrotu, a jej wielkość jest cosinusem połowy kąta obrotu. Każdy obrót jest reprezentowany przez dwa kwaterniony jednostkowe o przeciwnych znakach i, podobnie jak w przestrzeni obrotów w trzech wymiarach, iloczyn kwaternionów dwóch kwaternionów jednostkowych da kwaternion jednostkowy. Ponadto przestrzeń kwaternionów jednostkowych jest „płaska” w dowolnym nieskończenie małym sąsiedztwie danego kwaternionu jednostkowego.

Parametryzacja przestrzeni obrotów

Możemy sparametryzować powierzchnię kuli za pomocą dwóch współrzędnych, takich jak szerokość i długość geograficzna. Ale szerokość i długość geograficzna są niewłaściwie ( zdegenerowane ) na biegunie północnym i południowym, chociaż bieguny nie różnią się wewnętrznie od żadnych innych punktów na kuli. Na biegunach (szerokości geograficzne +90° i -90°) długość geograficzna traci znaczenie.

Można wykazać, że żaden dwuparametrowy układ współrzędnych nie pozwala uniknąć takiej degeneracji. Możemy uniknąć takich problemów osadzając kulę w przestrzeni trójwymiarowej i parametryzując ją trzema współrzędnymi kartezjańskimi ( w , x , y ) , umieszczając biegun północny w ( w , x , y ) = (1, 0, 0) , biegun południowy w ( w , x , y ) = (-1, 0, 0) i równik w w = 0 , x ² + y ² = 1 . Punkty na kuli spełniają ograniczenie w ² + x ² + y ² = 1 , więc nadal mamy tylko dwa stopnie swobody , chociaż istnieją trzy współrzędne. Punkt ( w , x , y ) na kuli reprezentuje obrót w zwykłej przestrzeni wokół osi poziomej skierowanej przez wektor ( x , y , 0) o kąt ${\ Displaystyle \ alfa = 2 \ cos ^ {-1} w = 2 \ grzech ^ {- 1} {\ sqrt {x ^ { 2}+y^{2}}}}$ .

W ten sam sposób przestrzeń hipersferyczną obrotów 3D można sparametryzować za pomocą trzech kątów ( kątów Eulera ), ale każda taka parametryzacja jest zdegenerowana w niektórych punktach hipersfery, co prowadzi do problemu blokady gimbala . Możemy tego uniknąć, używając czterech współrzędnych euklidesowych w , x , y , z , gdzie w ² + x ² + y ² + z ² = 1 . Punkt ( w , x , y , z ) reprezentuje obrót wokół osi kierowanej przez wektor ( x , y , z ) o kąt ${\ Displaystyle \ alfa = 2 \ bo ^ {-1} w = 2 \ grzech ^ {- 1} {\ sqrt {x ^ {2} + y ^ {2} + z ^ {2}}}.}$

Wyjaśnianie właściwości kwaternionów za pomocą rotacji

Nieprzemienność

Mnożenie kwaternionów jest nieprzemienne . Fakt ten wyjaśnia, jak p ↦ q p q ⁻¹ może w ogóle działać, mając z definicji q q ⁻¹ = 1 . Ponieważ mnożenie kwaternionów jednostkowych odpowiada składaniu rotacji trójwymiarowych, właściwość tę można uczynić intuicyjną, pokazując, że rotacje trójwymiarowe w ogóle nie są przemienne.

Ustaw dwie książki obok siebie. Obróć jeden z nich o 90 stopni zgodnie z ruchem wskazówek zegara wokół z , a następnie odwróć go o 180 stopni wokół osi x . Weź drugą książkę i obróć ją najpierw o 180° wokół osi x , a później o 90° zgodnie z ruchem wskazówek zegara wokół osi z . Obie książki nie kończą się równolegle. To pokazuje, że ogólnie rzecz biorąc, złożenie dwóch różnych obrotów wokół dwóch odrębnych osi przestrzennych nie będzie się zmieniać.

Orientacja

Iloczyn wektorowy wektorowy , używany do zdefiniowania reprezentacji osi i kąta, rzeczywiście nadaje przestrzeni orientację („ręczność”): w trójwymiarowej przestrzeni wektorowej trzy wektory w równaniu a × b = c zawsze będą tworzyć prawą zbiór -ręczny (lub zbiór lewoskrętny, w zależności od definicji iloczynu krzyżowego), ustalający w ten sposób orientację w przestrzeni wektorowej. Alternatywnie zależność od orientacji wyraża się w odniesieniu do takiego, który określa obrót co do ${\ displaystyle {\ vec {u}}}$ wektory osiowe . W formalizmie kwaternionowym wybór orientacji przestrzeni odpowiada porządkowi mnożenia: ij = k ale ji = − k . Jeśli odwrócimy orientację, wówczas powyższy wzór przyjmie postać   p ↦ q ⁻¹ p q , tj. jednostka q zostanie zastąpiona kwaternionem sprzężonym – zachowuje się tak samo jak wektory osiowe.

Alternatywne konwencje

Donoszono, że istnienie i dalsze stosowanie alternatywnej konwencji kwaternionów w przemyśle lotniczym i, w mniejszym stopniu, w społeczności robotyki wiąże się ze znacznymi i ciągłymi kosztami [ sic !]. Ta alternatywna konwencja została zaproponowana przez Shustera MD i odchodzi od tradycji, odwracając definicję mnożenia elementów podstawy kwaternionów w taki sposób, że zgodnie z konwencją Shustera ja $\ displaystyle \ mathbf {i} \ mathbf {j} = - \ mathbf {k} }$ , podczas gdy definicja Hamiltona to ${\ displaystyle \ mathbf {i} \ mathbf {j} = \ mathbf {k}$ } Konwencja ta jest również nazywana „konwencją JPL” ze względu na jej zastosowanie w niektórych częściach Laboratorium Napędów Odrzutowych NASA .

Zgodnie z konwencją Shustera wzór na pomnożenie dwóch kwaternionów zostaje zmieniony w taki sposób, że

${\ Displaystyle \ lewo (r_ {1}, \ {\ vec {v}} _ {1} \ prawo) \ lewo (r_ {2}, \ {\ vec {v}} _{2}\right)=\left(r_{1}r_{2}-{\vec {v}}_{1}\cdot {\vec {v}}_{2},\ r_{1} {\vec {v}}_{2}+r_{2}{\vec {v}}_{1}\mathbin {\color {red}\mathbf {-} } {\vec {v}}_{ 1}\times {\vec {v}}_{2}\right),\qquad {\text{(Alternatywna konwencja, odradzamy używanie!)}}}$

Wzór na obrót wektora o kwaternion zostaje zmieniony na:

${\ Displaystyle {\ początek {wyrównane} \ mathbf {p} '_ {\ tekst {alt}} = {} & (\ mathbf {v} \ otimes \ mathbf {v} + q_ {r} ^ {2} \ mathbf {I} \mathbin {\color {czerwony}\mathbf {-} } 2q_{r}[\mathbf {v} ]_{\times }+[\mathbf {v} ]_{\times }^{2 })\mathbf {p} &{\text{(Alternatywna konwencja, odradzamy użycie!)}}\\=&\ (\mathbf {I} \mathbin {\color {red}\mathbf {-} } 2q_{r }[\mathbf {v} ]_{\times }+2[\mathbf {v} ]_{\times }^{2})\mathbf {p} &\end{aligned}}}$

Aby zidentyfikować zmiany zgodnie z konwencją Shustera, zobacz, że znak przed iloczynem krzyżowym jest odwrócony z plusa na minus.

Na koniec zmienia się wzór na konwersję kwaternionu na macierz rotacji

${\ Displaystyle {\ początek {wyrównane} \ mathbf {R} _ {alt} i = \ mathbf {I} \ mathbin {\ kolor {czerwony} \ mathbf {-}} 2q_ {r} [\ mathbf {v}] _{\times }+2[\mathbf {v} ]_{\times }^{2}\qquad {\text{(Alternatywna konwencja, odradzamy używanie!)}}\\&={\begin{bmatrix}1 -2s(q_{j}^{2}+q_{k}^{2})&2(q_{i}q_{j}+q_{k}q_{r})&2(q_{i}q_{k }-q_{j}q_{r})\\2(q_{i}q_{j}-q_{k}q_{r})&1-2s(q_{i}^{2}+q_{k} ^{2})&2(q_{j}q_{k}+q_{i}q_{r})\\2(q_{i}q_{k}+q_{j}q_{r})&2(q_ {j}q_{k}-q_{i}q_{r})&1-2s(q_{i}^{2}+q_{j}^{2})\end{bmatrix}}\end{aligned} }}$

co jest dokładnie transpozycją macierzy rotacji przeliczonej zgodnie z tradycyjną konwencją.

Aplikacje programowe według stosowanej konwencji

Poniższa tabela grupuje aplikacje według ich zgodności z konwencją kwaternionów:

Konwencja mnożenia Hamiltona	Konwencja mnożenia Shustera
Wolframa Mathematica Zestaw narzędzi systemu robotyki MATLAB Przybornik lotniczy MATLAB ROS Własny Wzmocnij kwaterniony Quaternion.js Solver Ceres Biblioteka SciPy przestrzenna.transform.Rotation Biblioteka matematyki symbolicznej SymPy biblioteka numpy-quaternion	Biblioteka matematyczna Microsoft DirectX

Choć użycie żadnej konwencji nie wpływa na możliwości i poprawność tworzonych w ten sposób aplikacji, autorzy argumentowali, że należy porzucić konwencję Shustera, ponieważ odbiega ona od znacznie starszej konwencji mnożenia kwaternionów Hamiltona i może nigdy nie zostać przyjęta przez świat matematyczny lub teoretyczny obszary fizyki.

Porównanie z innymi reprezentacjami obrotów

Zalety kwaternionów

Reprezentacja rotacji w postaci kwaternionu (4 liczby) jest bardziej zwarta niż reprezentacja w postaci macierzy ortogonalnej (9 liczb). Co więcej, dla danej osi i kąta można łatwo skonstruować odpowiedni kwaternion i odwrotnie, dla danego kwaternionu można łatwo odczytać oś i kąt. Obydwa są znacznie trudniejsze w przypadku macierzy lub kątów Eulera .

W grach wideo i innych zastosowaniach często interesują nas „płynne obroty”, co oznacza, że ​​scena powinna obracać się powoli, a nie w jednym kroku. Można to osiągnąć wybierając krzywą , taką jak sferyczna interpolacja liniowa w kwaternionach, przy czym jednym punktem końcowym jest transformacja tożsamości 1 (lub inny obrót początkowy), a drugim jest zamierzony obrót końcowy. Jest to bardziej problematyczne w przypadku innych reprezentacji obrotów.

Podczas komponowania kilku obrotów na komputerze błędy zaokrągleń koniecznie się kumulują. Kwaternion, który jest nieco przesunięty, nadal reprezentuje rotację po normalizacji: macierz, która jest nieco odchylona, ​​może nie być już ortogonalna i trudniej jest ją przekonwertować z powrotem do właściwej macierzy ortogonalnej.

Kwaterniony unikają również zjawiska zwanego blokadą przegubu Cardana , które może wystąpić, gdy na przykład w układach obrotowych typu pitch/yaw/roll nachylenie jest obracane o 90° w górę lub w dół, tak że odchylenie i przechylenie odpowiadają temu samemu ruchowi, a stopień swoboda obrotu zostaje utracona. Na przykład w lotniczym systemie nawigacji inercyjnej opartym na przegubie Cardana może to mieć katastrofalne skutki, jeśli statek powietrzny gwałtownie nurkuje lub wznosi się.

Konwersja do i z reprezentacji macierzowej

Od kwaternionu do macierzy ortogonalnej

Macierz ortogonalna odpowiadająca obrotowi o kwaternion jednostkowy     z = a + b i + c j + d k (przy |   z   | = 1 ) po mnożeniu przez wektor kolumnowy jest dana wzorem

${\ Displaystyle R = {\ początek {pmatrix} a ^ {2} + b ^ {2} -c ^ {2} -d ^ {2} i 2bc-2ad i 2bd + 2ac \\ 2bc + 2ad i a ^ {2} -b ^{2}+c^{2}-d^{2}&2cd-2ab\\2bd-2ac&2cd+2ab&a^{2}-b^{2}-c^{2}+d^{2}\\ \end{pmatrix}}.}$

Ta macierz rotacji jest używana na wektorze w jako ${\ displaystyle w _ {\ tekst {obrócony}} = R \ cdot w}$ . Kwaternionową reprezentację tego obrotu podaje wzór:

${\ Displaystyle {\ początek {bmatrix} 0 \\ w _ {\ tekst {obrócony}} \ koniec {bmatrix}} = z {\ początek {bmatrix} 0 \\ w \end{bmatrix}}z^{*},}$

gdzie $_ *}=ab\mathbf {i} -c\mathbf {j} -d\mathbf {k} }$ koniugatem $kwaternionu$ przez $\$

Ponadto mnożenie kwaternionów definiuje się jako (zakładając, że a i b są kwaternionami, jak z powyżej):

${\ Displaystyle ab = \ lewo (a_ {0} b_ {0} - {\ vec {a} }\cdot {\vec {b}};a_{0}{\vec {b}}+b_{0}{\vec {a}}+{\vec {a}}\times {\vec {b} }\Prawidłowy)}$

gdzie rząd a , b jest ważny, ponieważ iloczyn krzyżowy dwóch wektorów nie jest przemienny.

Bardziej efektywne obliczenie, w którym kwaternion nie musi być znormalizowany jednostkowo, jest podane przez

${\ Displaystyle R = {\ początek {pmatrix} 1-cc-dd i bc-ad i bd + ac \\ bc + reklama i 1-bb-dd i cd-ab \\ bd-ac i cd + ab i 1-bb-cc \\\ koniec { pmatrix}},}$

gdzie określono następujące wielkości pośrednie:

${\ Displaystyle {\ początek {alignedat} {2} i \ \ s = 2 / (a ​​\ cdot a + b \ cdot b + c \ cdot c + d \ cdot d), \\ & {\ początek {tablica} {lll}bs=b\cdot s,&cs=c\cdot s,&ds=d\cdot s,\\ab=a\cdot bs,&ac=a\cdot cs,&ad=a\cdot ds,\\bb =b\cdot bs,&bc=b\cdot cs,&bd=b\cdot ds,\\cc=c\cdot cs,&cd=c\cdot ds,&dd=d\cdot ds.\\\end{array} }\end{alignedat}}}$

Od macierzy ortogonalnej do kwaternionu

Należy zachować ostrożność podczas konwersji macierzy rotacji na kwaternion, ponieważ kilka prostych metod jest zwykle niestabilnych, gdy ślad ( suma elementów przekątnych) macierzy rotacji jest zerowy lub bardzo mały. Aby zapoznać się ze stabilną metodą konwersji macierzy ortogonalnej na kwaternion, zobacz macierz rotacji#Kwaternion .

Dopasowanie kwaternionów

W powyższej sekcji opisano, jak odzyskać kwaternion q z macierzy rotacji 3 × 3 Q . Załóżmy jednak, że mamy pewną macierz Q , która nie jest czystą rotacją – na przykład z powodu błędów zaokrągleń – i chcemy znaleźć kwaternion q , który najdokładniej reprezentuje Q . W takim przypadku konstruujemy symetryczną macierz 4 × 4

${\ Displaystyle K = {\ Frac {1} {3}} {\ początek {bmatrix} Q_ {xx} -Q_ {yy} -Q_ {zz} i Q_ {yx} + Q_ {xy} i Q_ {zx} + Q_ {xz}&Q_{zy}-Q_{yz}\\Q_{yx}+Q_{xy}&Q_{yy}-Q_{xx}-Q_{zz}&Q_{zy}+Q_{yz}&Q_{xz} -Q_{zx}\\Q_{zx}+Q_{xz}&Q_{zy}+Q_{yz}&Q_{zz}-Q_{xx}-Q_{yy}&Q_{yx}-Q_{xy}\\ Q_{zy}-Q_{yz}&Q_{xz}-Q_{zx}&Q_{yx}-Q_{xy}&Q_{xx}+Q_{yy}+Q_{zz}\end{bmatrix}},}$

i znajdź wektor własny ( x , y , z , w ) odpowiadający największej wartości własnej (ta wartość będzie wynosić 1 wtedy i tylko wtedy, gdy Q jest czystym obrotem). Otrzymany w ten sposób kwaternion będzie odpowiadał rotacji najbliższej pierwotnej macierzy Q .

Porównania wydajności

W tej sekcji omówiono konsekwencje wydajnościowe stosowania kwaternionów w porównaniu z innymi metodami (macierze osi/kąta lub obrotu) do wykonywania obrotów w 3D.

Wyniki

Wymagania dotyczące przechowywania

metoda	Składowanie
Macierz rotacyjna	9
Kwaternion	3 lub 4 (patrz poniżej)
Oś kątowa	3 lub 4 (patrz poniżej)

Tylko trzy składniki kwaternionów są niezależne, ponieważ obrót jest reprezentowany przez kwaternion jednostkowy. Do dalszych obliczeń zwykle potrzebne są wszystkie cztery elementy, zatem wszystkie obliczenia wiązałyby się z dodatkowymi kosztami w przypadku odzyskania czwartego składnika. Podobnie oś kąta można zapisać w wektorze trójskładnikowym, mnożąc kierunek jednostki przez kąt (lub jego funkcję), ale wiąże się to z dodatkowymi kosztami obliczeniowymi w przypadku używania jej do obliczeń.

Porównanie wydajności operacji łączenia rotacji

metoda	# mnoży się	# dodaj/odejmij	ogółem operacji
Macierze rotacyjne	27	18	45
Kwaterniony	16	12	28

Porównanie wydajności operacji obracania wektorów

metoda		# mnoży się	# dodaj/odejmij	# grzech/cos	ogółem operacji
Macierz rotacyjna		9	6	0	15
Kwaterniony *	Bez matrycy pośredniej	15	15	0	30
	Z matrycą pośrednią	21	18	0	39
Oś kątowa	Bez matrycy pośredniej	18	13	2	30 + 3
	Z matrycą pośrednią	21	16	2	37 + 2

* Kwaterniony można w sposób dorozumiany przekształcić w macierz rotacyjną (12 mnożeń i 12 dodawania/odejmowań), która wyrównuje koszt rotacji następujących wektorów metodą macierzy rotacji.

Stosowane metody

Istnieją trzy podstawowe podejścia do obracania wektora v → :

1. Oblicz iloczyn macierzowy macierzy rotacji 3 × 3 R i pierwotnej macierzy kolumnowej 3 × 1 reprezentującej v → . Wymaga to 3 × (3 mnożenia + 2 dodawania) = 9 mnożeń i 6 dodawania, co jest najbardziej efektywną metodą obracania wektora.
2. Obrót można przedstawić za pomocą kwaternionu o jednostkowej długości q = ( w , r → ) z częścią skalarną (rzeczywistą) w i częścią wektorową (urojoną) r → . Obrót można zastosować do wektora 3D v → za pomocą wzoru ${\ Displaystyle {\ vec {v}} _ {\ tekst {nowy}} = {\ vec {v}} + 2 {\ vec {r}} \ razy ({\ vec {r}} \ razy {\ vec {v}}+w{\vec {v}})}$ . Wymaga to jedynie 15 mnożeń i 15 dodań do obliczenia (lub 18 mnożeń i 12 dodań, jeśli współczynnik 2 odbywa się poprzez mnożenie). Ten wzór, pierwotnie uważany za używany z notacją osi/kąta (wzór Rodriguesa), może być również stosowane do notacji kwaternionów. Daje to taki sam wynik, jak mniej wydajny, ale bardziej zwarty wzór na mnożenie kwaternionów ${\ Displaystyle {\ vec {v}} _ {\ tekst {nowy}} = q {\ vec {v}} q ^ {-1}}$ .
3. Użyj wzoru na kąt/oś , aby przekonwertować kąt/oś na macierz obrotu R , a następnie pomnóż przez wektor, lub podobnie użyj wzoru, aby przekonwertować zapis kwaternionów na macierz obrotu, a następnie pomnóż przez wektor. Konwersja kąta/osi na R kosztuje 12 mnożeń, 2 wywołania funkcji (sin, cos) i 10 dodawania/odejmowania; z punktu 1, obracanie za pomocą R dodaje dodatkowych 9 mnożeń i 6 dodań, co daje w sumie 21 mnożeń, 16 dodawania/odejmowania i 2 wywołania funkcji (sin, cos). Konwersja kwaternionu na R kosztuje 12 mnożeń i 12 dodawania/odejmowania; z punktu 1, obracanie za pomocą R dodaje dodatkowych 9 mnożeń i 6 dodań, co daje w sumie 21 mnożeń i 18 dodawania/odejmowań.

Porównanie wydajności n wektorów operacji obrotowych

metoda		# mnoży się	# dodaj/odejmij	# grzech/cos	ogółem operacji
Macierz rotacyjna		9 rz	6 rz	0	15 n
Kwaterniony *	Bez matrycy pośredniej	15 n	15 n	0	30 n
	Z matrycą pośrednią	9 n + 12	6 n + 12	0	15 n + 24
Oś kątowa	Bez matrycy pośredniej	18 n	12 n + 1	2	30 n + 3
	Z matrycą pośrednią	9 n + 12	6 n + 10	2	15 n + 24

Pary kwaternionów jednostkowych jako rotacje w przestrzeni 4D

Para kwaternionów jednostkowych z _l i z _r może reprezentować dowolny obrót w przestrzeni 4D . Mając czterowymiarowy wektor v → i zakładając, że jest to kwaternion, możemy obrócić wektor v → w następujący sposób:

${\ Displaystyle f \ lewo ({\ vec {v}} \ prawo) = \ mathbf {z} _ {\ rm {l}} \ vec {v}} \ mathbf {z} _ {\ rm {r} }={\begin{pmatrix}a_{\rm {l}}&-b_{\rm {l}}&-c_{\rm {l}}&-d_{\rm {l}}\\b_{ \rm {l}}&a_{\rm {l}}&-d_{\rm {l}}&c_{\rm {l}}\\c_{\rm {l}}&d_{\rm {l}} &a_{\rm {l}}&-b_{\rm {l}}\\d_{\rm {l}}&-c_{\rm {l}}&b_{\rm {l}}&a_{\rm {l}}\end{pmatrix}}{\begin{pmatrix}w\\x\\y\\z\end{pmatrix}}{\begin{pmatrix}a_{\rm {r}}&-b_{ \rm {r}}&-c_{\rm {r}}&-d_{\rm {r}}\\b_{\rm {r}}&a_{\rm {r}}&d_{\rm {r }}&-c_{\rm {r}}\\c_{\rm {r}}&-d_{\rm {r}}&a_{\rm {r}}&b_{\rm {r}}\\ d_{\rm {r}}&c_{\rm {r}}&-b_{\rm {r}}&a_{\rm {r}}\end{pmatrix}}.}$

Para macierzy reprezentuje obrót ℝ ⁴ . Zauważ, że ponieważ ${\ Displaystyle (\ mathbf {z} _ {\ rm {l}} {\ vec {v}}) \ mathbf {z} _{\rm {r}}=\mathbf {z} _{\rm {l}}({\vec {v}}\mathbf {z} _{\rm {r}})} , obie macierze$ muszą dojeżdżać. Dlatego też istnieją dwie podgrupy dojeżdżających do pracy grupy czterowymiarowych rotacji. Dowolne czterowymiarowe obroty mają 6 stopni swobody; każda macierz reprezentuje 3 z tych 6 stopni swobody.

Ponieważ generatory czterowymiarowych rotacji można przedstawić za pomocą par kwaternionów (w następujący sposób), można również przedstawić wszystkie czterowymiarowe rotacje.

${\ Displaystyle {\ początek {wyrównane} \ mathbf {z} _ {\ rm {l}} {\ vec {v}} \ mathbf {z} _ {\ rm {r}} i = {\ początek {pmatrix} 1&-dt_{ab}&-dt_{ac}&-dt_{ad}\\dt_{ab}&1&-dt_{bc}&-dt_{bd}\\dt_{ac}&dt_{bc}&1&-dt_{ cd}\\dt_{ad}&dt_{bd}&dt_{cd}&1\end{pmatrix}}{\begin{pmatrix}w\\x\\y\\z\end{pmatrix}}\\[3pt] \mathbf {z} _{\rm {l}}&=1+{dt_{ab}+dt_{cd} \over 2}i+{dt_{ac}-dt_{bd} \over 2}j+{dt_{ ad}+dt_{bc} \over 2}k\\[3pt]\mathbf {z} _{\rm {r}}&=1+{dt_{ab}-dt_{cd} \over 2}i+{ dt_{ac}+dt_{bd} \over 2}j+{dt_{ad}-dt_{bc} \over 2}k\end{aligned}}}$

Zobacz też

• Mechanizm zapobiegający skręcaniu
• Binarna grupa wielościenna
• Bikwaternion
• Wykresy na SO(3)
• Algebry Clifforda
• Konwersja kwaternionów na kąty Eulera
• Zakrywanie przestrzeni
• Podwójny kwaternion
• Liczba podwójnie zespolona
• Geometria eliptyczna
• Formalizmy rotacyjne w trzech wymiarach
• Obrót (matematyka)
• Grupa spinowa
• Slerp , sferyczna interpolacja liniowa
• Olinde Rodrigues
• Williama Rowana Hamiltona

Dalsza lektura

• Grubin, Carl (1970). „Wyprowadzenie schematu kwaternionów za pomocą osi i kąta Eulera”. Dziennik statków kosmicznych i rakiet . 7 (10): 1261–1263. Bibcode : 1970JSpRo...7.1261G . doi : 10,2514/3,30149 .
•   Battey-Pratt, EP; Racey, TJ (1980). „Model geometryczny cząstek podstawowych”. International Journal of Fizyki Teoretycznej . 19 (6): 437–475. Kod Bib : 1980IJTP...19..437B . doi : 10.1007/BF00671608 . S2CID 120642923 .

•   Arribas, M.; Elipe, A.; Palacios, M. (2006). „Kwaterniony i obroty ciała sztywnego”. Celeste. Mech. Dyn. Astron . 96 (3–4): 239–251. Kod Bib : 2006CeMDA..96..239A . doi : 10.1007/s10569-006-9037-6 . S2CID 123591599 .

Zewnętrzne linki i zasoby

• Szewc, Ken. „Kwaterniony” (PDF) . Zarchiwizowane (PDF) od oryginału w dniu 2020-05-03.
• „Prosty typ kwaternionów i operacje w ponad siedemdziesięciu pięciu językach komputerowych” . w sprawie Kodeksu Rosetty
• Hart, John C. „Demonstrator kwaternionów” .
• Dam, Eik B.; Koch, Martin; Lillholm, Martin (1998). „Kwaterniony, interpolacja i animacja” (PDF) .
• Leandra, Vicci (2001). „Kwaterniony i obroty w 3 przestrzeni: algebra i jej interpretacja geometryczna” (PDF) .
• Howell, Thomas; Lafon, Jean-Claude (1975). „Złożoność produktu czwartorzędowego, TR75-245” (PDF) . Uniwersytet Cornella.
• Róg, Berthold KP (2001). „Kilka uwag na temat kwaternionów jednostek i rotacji” (PDF) .
• Lee, Byung-Uk (1991). Kwaternion jednostkowy Reprezentacja rotacji - Załącznik A, Różniczkowanie za pomocą kwaternionów - Załącznik B (PDF) (praca doktorska). Uniwersytet Stanford.
• Vance, Rod. „Kilka przykładów połączonych grup Liego” . Zarchiwizowane od oryginału w dniu 2018-12-15.
• „Wizualne przedstawienie rotacji kwaternionów” .