Geometria eliptyczna

Geometria eliptyczna jest przykładem geometrii, w której równoległy postulat Euklidesa nie jest spełniony. Zamiast tego, podobnie jak w geometrii sferycznej , nie ma linii równoległych, ponieważ dowolne dwie linie muszą się przecinać. Jednak w przeciwieństwie do geometrii sferycznej zwykle zakłada się, że dwie linie przecinają się w jednym punkcie (a nie w dwóch). Z tego powodu geometria eliptyczna opisana w tym artykule jest czasami określana jako pojedyncza geometria eliptyczna, podczas gdy geometria sferyczna jest czasami określana jako geometria podwójnie eliptyczna .

Pojawienie się tej geometrii w XIX wieku pobudziło rozwój geometrii nieeuklidesowej w ogóle, w tym geometrii hiperbolicznej .

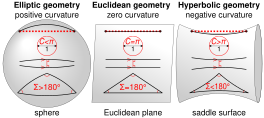
Geometria eliptyczna ma wiele właściwości, które różnią się od właściwości klasycznej geometrii płaszczyzny euklidesowej. Na przykład suma kątów wewnętrznych dowolnego trójkąta jest zawsze większa niż 180°.

Definicje

W geometrii eliptycznej dwie proste prostopadłe do danej prostej muszą się przecinać. W rzeczywistości wszystkie prostopadłe po jednej stronie przecinają się w jednym punkcie zwanym biegunem absolutnym tej linii. Prostopadłe po drugiej stronie również przecinają się w jednym punkcie. Jednak w przeciwieństwie do geometrii sferycznej bieguny po obu stronach są takie same. Dzieje się tak, ponieważ w geometrii eliptycznej nie ma punktów antypodalnych . Na przykład osiąga się to w modelu hipersferycznym (opisanym poniżej) poprzez uczynienie „punktów” w naszej geometrii faktycznie parami przeciwległych punktów na kuli. Powodem tego jest to, że pozwala geometrii eliptycznej spełnić aksjomat, że istnieje niepowtarzalna linia przechodząca przez dowolne dwa punkty.

Każdy punkt odpowiada absolutnej linii biegunowej , której jest biegunem absolutnym. Dowolny punkt na tej linii biegunowej tworzy absolutną parę sprzężoną z biegunem. Taka para punktów jest ortogonalna , a odległość między nimi to ćwiartka .

Odległość między parą punktów jest proporcjonalna do kąta między ich biegunami bezwzględnymi .

Jak wyjaśnił HSM Coxeter :

Nazwa „eliptyczny” jest prawdopodobnie myląca. Nie oznacza to żadnego bezpośredniego związku z krzywą zwaną elipsą, a jedynie dość naciąganą analogię. Centralny stożek nazywany jest elipsą lub hiperbolą, ponieważ nie ma asymptoty lub ma dwie asymptoty . Analogicznie, o płaszczyźnie nieeuklidesowej mówi się, że jest eliptyczna lub hiperboliczna, ponieważ każda z jej linii nie zawiera żadnego punktu w nieskończoności lub dwóch punktów w nieskończoności.

Dwa wymiary

Płaszczyzna eliptyczna

Płaszczyzna eliptyczna jest rzeczywistą płaszczyzną rzutową wyposażoną w metrykę . Kepler i Desargues wykorzystali projekcję gnomoniczną , aby powiązać płaszczyznę σ z punktami na stycznej do niej półkuli . Gdy O jest środkiem półkuli, punkt P w σ wyznacza prostą OP przecinającą półkulę, a każda prosta L ⊂ σ wyznacza płaszczyznę OL , która przecina półkulę w połowie wielkiego koła . Półkula jest ograniczona płaszczyzną przechodzącą przez O i równoległą do σ. Żadna zwykła linia σ nie odpowiada tej płaszczyźnie; zamiast tego σ dołączana jest linia w nieskończoności . Ponieważ każda prosta w tym przedłużeniu σ odpowiada płaszczyźnie przechodzącej przez O , a każda para takich płaszczyzn przecina się w linii przechodzącej przez O , można wywnioskować, że dowolna para prostych w przedłużeniu przecina się: punkt przecięcia leży tam, gdzie płaszczyzna przecięcie spotyka σ lub linię w nieskończoności. W ten sposób potwierdza się aksjomat geometrii rzutowej, zgodnie z którym wszystkie pary prostych na płaszczyźnie muszą się przecinać.

Biorąc pod uwagę P i Q w σ , eliptyczna odległość między nimi jest miarą kąta POQ , przyjmowaną zwykle w radianach. Arthur Cayley zainicjował badanie geometrii eliptycznej, kiedy napisał „O definicji odległości”. To przedsięwzięcie w kierunku abstrakcji w geometrii było kontynuowane przez Felixa Kleina i Bernharda Riemanna, co doprowadziło do geometrii nieeuklidesowej i geometrii riemannowskiej .

Porównanie z geometrią euklidesową

Porównanie geometrii eliptycznej, euklidesowej i hiperbolicznej w dwóch wymiarach

W geometrii euklidesowej figurę można powiększać lub zmniejszać w nieskończoność, a otrzymane figury są podobne, tj. mają te same kąty i te same proporcje wewnętrzne. W geometrii eliptycznej tak nie jest. Na przykład w modelu sferycznym widzimy, że odległość między dowolnymi dwoma punktami musi być ściśle mniejsza niż połowa obwodu kuli (ponieważ punkty antypodalne są identyfikowane). Dlatego segment linii nie może być skalowany w nieskończoność. Geometr mierzący właściwości geometryczne przestrzeni, którą zamieszkuje, może wykryć za pomocą pomiarów, że istnieje pewna skala odległości, która jest właściwością przestrzeni. W skalach znacznie mniejszych niż ta, przestrzeń jest w przybliżeniu płaska, geometria jest w przybliżeniu euklidesowa, a figury można powiększać i zmniejszać, pozostając w przybliżeniu podobnymi.

Wiele geometrii euklidesowej przenosi się bezpośrednio do geometrii eliptycznej. Na przykład pierwszy i czwarty z postulatów Euklidesa, że między dowolnymi dwoma punktami istnieje niepowtarzalna linia i że wszystkie kąty proste są równe, obowiązują w geometrii eliptycznej. Postulat 3, że można skonstruować okrąg o dowolnym środku i promieniu, zawodzi, jeśli „dowolny promień” oznacza „dowolną liczbę rzeczywistą”, ale obowiązuje, jeśli ma oznaczać „długość dowolnego danego odcinka linii”. Dlatego każdy wynik w geometrii euklidesowej, który wynika z tych trzech postulatów, będzie miał zastosowanie w geometrii eliptycznej, na przykład twierdzenie 1 z księgi I Elementów , które stwierdza , że mając dowolny odcinek linii, można zbudować trójkąt równoboczny z odcinkiem jako podstawą.

Geometria eliptyczna jest również podobna do geometrii euklidesowej, ponieważ przestrzeń jest ciągła, jednorodna, izotropowa i bez granic. Izotropię gwarantuje czwarty postulat, że wszystkie kąty proste są sobie równe. Jako przykład jednorodności zauważ, że twierdzenie Euklidesa I.1 implikuje, że ten sam trójkąt równoboczny można zbudować w dowolnym miejscu, a nie tylko w miejscach, które są w jakiś sposób specjalne. Brak granic wynika z drugiego postulatu, rozciągliwości odcinka linii.

Jednym ze sposobów, w jaki geometria eliptyczna różni się od geometrii euklidesowej, jest to, że suma kątów wewnętrznych trójkąta jest większa niż 180 stopni. Na przykład w modelu sferycznym można zbudować trójkąt z wierzchołkami w miejscach, w których trzy dodatnie osie współrzędnych kartezjańskich przecinają kulę, a wszystkie trzy jego wewnętrzne kąty mają 90 stopni, co daje łącznie 270 stopni. W przypadku wystarczająco małych trójkątów nadmiar ponad 180 stopni można dowolnie zmniejszyć.

Twierdzenie Pitagorasa zawodzi w geometrii eliptycznej. W opisanym powyżej trójkącie 90 ° –90 ° –90 ° wszystkie trzy boki mają tę samą długość, w związku z czym nie spełniają za $\ Displaystyle a ^ {2} + b ^ {2} = c^{2}}$ . Wynik Pitagorasa jest odzyskiwany w granicach małych trójkątów.

Stosunek obwodu koła do jego pola jest mniejszy niż w geometrii euklidesowej. Ogólnie rzecz biorąc, powierzchnia i objętość nie skalują się jako druga i trzecia potęga wymiarów liniowych.

Przestrzeń eliptyczna (przypadek 3D)

Uwaga: w tej sekcji termin „przestrzeń eliptyczna” odnosi się konkretnie do trójwymiarowej geometrii eliptycznej. Kontrastuje to z poprzednią sekcją, która dotyczyła dwuwymiarowej geometrii eliptycznej. Kwaterniony służą do wyjaśnienia tej przestrzeni.

Przestrzeń eliptyczną można skonstruować w sposób podobny do konstrukcji trójwymiarowej przestrzeni wektorowej: z klasami równoważności . Używa się skierowanych łuków na wielkich kołach kuli. Ponieważ skierowane odcinki linii są równoważne , gdy są równoległe, tej samej długości i podobnie zorientowane, tak skierowane łuki znalezione na kołach wielkich są równoważne, gdy mają tę samą długość, orientację i koło wielkie. Te relacje równoważności tworzą odpowiednio przestrzeń wektorową 3D i przestrzeń eliptyczną.

Dostęp do struktury przestrzeni eliptycznej zapewnia algebra wektorów Williama Rowana Hamiltona : wyobraził sobie kulę jako dziedzinę pierwiastków kwadratowych minus jeden. Wtedy wzór Eulera ${\ Displaystyle \ exp (\ theta r) = \ cos \ theta + r \ sin \ theta}$ (gdzie r jest na kuli) reprezentuje koło wielkie na płaszczyźnie zawierającej 1 i r . Przeciwne punkty r i – r odpowiadają okręgom o przeciwnych kierunkach. Łuk między θ a φ jest równy łukowi między 0 a φ – θ. W przestrzeni eliptycznej długość łuku jest mniejsza niż π, więc łuki można parametryzować za pomocą θ w [0, π) lub (–π/2, π/2).

dla ${\ Displaystyle z = \ exp (\ theta r), \ z ^ {*} = \ exp ( -\theta r)\implikuje zz^{*}=1.}$ Mówi się, że moduł lub norma z wynosi jeden (Hamilton nazwał to tensorem z). Ale ponieważ r rozciąga się na kuli w 3-przestrzeni, exp(θ r) rozciąga się na kuli w 4-przestrzeni, zwanej teraz 3 -sferą , ponieważ jej powierzchnia ma trzy wymiary. Hamilton nazwał swoją algebrę czwartorzędami i szybko stała się ona użytecznym i cenionym narzędziem matematyki. $t$ przestrzeń ewoluuje z w liczbach _

Podczas wykonywania trygonometrii na Ziemi lub na sferze niebieskiej boki trójkątów są łukami wielkiego koła. Pierwszym sukcesem kwaternionów było przekształcenie trygonometrii sferycznej w algebrę. Hamilton nazwał quaternion o normie 1 versorem i są to punkty przestrzeni eliptycznej.

Przy ustalonym $r$ wersory

{\ Displaystyle e ^ {ar}, \ quad 0 \ równoważnik a <\ pi}

tworzą linię eliptyczną . Odległość od ${\ Displaystyle e ^ {ar}}$ do 1 $za$ . Dla dowolnego wersora $u$ odległość będzie równa odległości θ, dla której $cos θ = (u + u *)/2$ , ponieważ jest to wzór na część skalarną dowolnego kwaternionu.

Ruch eliptyczny jest opisany przez odwzorowanie kwaternionów

{\ Displaystyle q \ mapsto uqv,}

gdzie

u

i

v

są ustalonymi wersorami.

Odległości między punktami są takie same, jak między punktami obrazu ruchu eliptycznego. W przypadku, gdy $u$ i $v$ są wzajemnie sprzężonymi czwartorzędami, ruch jest obrotem przestrzennym , a ich część wektorowa jest osią obrotu. W przypadku $u =1$ ruch eliptyczny nazywany jest prawostronnym przesunięciem Clifforda lub parataksją . Przypadek $v = 1$ odpowiada lewostronnej translacji Clifforda.

Linie eliptyczne przechodzące przez versor $u$ mogą mieć postać

{\ Displaystyle \ lbrace ue ^ {ar}: 0 \ równoważnik a <\ pi \ rbrace}

lub

{\ Displaystyle \ lbrace e ^{ar}u:0\leq a<\pi \rbrace }

dla ustalonego

r

.

Są to prawe i lewe translacje u Clifforda $wzdłuż$ linii eliptycznej przechodzącej przez 1. Przestrzeń eliptyczna jest tworzona z $S 3$ poprzez identyfikację punktów antypodalnych.

Przestrzeń eliptyczna ma specjalne struktury zwane równoleżnikami Clifforda i powierzchniami Clifforda .

Punkty wersorowe przestrzeni eliptycznej są odwzorowywane przez transformatę Cayleya na ℝ ³ dla alternatywnej reprezentacji przestrzeni.

Przestrzenie o wyższych wymiarach

Model hipersferyczny

Model hipersferyczny jest uogólnieniem modelu sferycznego na wyższe wymiary. Punkty n -wymiarowej przestrzeni eliptycznej to pary wektorów jednostkowych $(x, - x)$ w R ^{n +1} , czyli pary antypodalnych punktów na powierzchni kuli jednostkowej w ( n + 1) -wymiarowej przestrzeni ( n - wymiarowa hipersfera). Linie w tym modelu są kołami wielkimi , czyli przecięciami hipersfery z płaskimi hiperpowierzchniami o wymiarze n przechodzącymi przez początek układu współrzędnych.

Rzutowa geometria eliptyczna

jako punkty modelu wykorzystywane są punkty n -wymiarowej rzeczywistej przestrzeni rzutowej . To modeluje abstrakcyjną geometrię eliptyczną, znaną również jako geometria rzutowa .

Punkty n -wymiarowej przestrzeni rzutowej można utożsamiać z liniami przechodzącymi przez początek w ( n + 1) -wymiarowej przestrzeni i można je reprezentować niejednoznacznie przez niezerowe wektory w R ^{n + 1} , przy założeniu, że $u$ i $λ u$ , dla dowolnego niezerowego skalara $λ$ , reprezentują ten sam punkt. Odległość jest definiowana za pomocą metryki

{\ Displaystyle d (u, v) = \ arccos \ lewo ({\ Frac {| u \ cdot v |} {\ | u \|\ \| v \|}} \ prawo);}

^{+1 między} dwoma punktami jest kątem między odpowiadającymi im prostymi w Rn . Formuła odległości jest jednorodna dla każdej zmiennej, gdzie $d (λ u, μ v) = d (u, v)$ , jeśli $λ$ i $μ$ są niezerowymi skalarami, więc definiuje odległość w punktach przestrzeni rzutowej.

Godną uwagi właściwością rzutowej geometrii eliptycznej jest to, że dla parzystych wymiarów, takich jak płaszczyzna, geometria jest nieorientowalna . Usuwa rozróżnienie między obrotami zgodnymi z ruchem wskazówek zegara i przeciwnie do ruchu wskazówek zegara, identyfikując je.

Model stereograficzny

Model reprezentujący tę samą przestrzeń co model hipersferyczny można otrzymać za pomocą rzutu stereograficznego . Niech E ⁿ reprezentuje R ⁿ ∪ {∞}, czyli $n$ -wymiarową przestrzeń rzeczywistą rozciągniętą o pojedynczy punkt w nieskończoności. Możemy zdefiniować metrykę, metrykę akordową , na E ⁿ przez

{\ Displaystyle \ delta (u, v) = {\ Frac {2 \| uv \ | }{\sqrt {(1+\|u\|^{2})(1+\|v\|^{2})}}}}

gdzie $u$ i $v są$ $jest$ wektorami w R ⁿ i normą euklidesową. Definiujemy również

{\ Displaystyle \ delta (u, \ infty) = \ delta (\ infty, u) = {\ Frac {2} {\ sqrt {1 + \ | u \ | ^ {2}}}}.}

Wynikiem jest przestrzeń metryczna na E ⁿ , która reprezentuje odległość wzdłuż cięciwy odpowiednich punktów na modelu hipersferycznym, do którego jest odwzorowywana bijektywnie przez projekcję stereograficzną. Model o geometrii sferycznej otrzymamy, jeśli użyjemy metryki

{\ Displaystyle d (u, v) = 2 \ arcsin \ lewo ({\ Frac {\ delta (u, v)} {2}} \ prawej).}

Z tego uzyskuje się geometrię eliptyczną, identyfikując antypodalne punkty $u$ i $- u / ‖ u ‖ 2$ i przyjmując odległość od $v$ do tej pary jako minimalną z odległości od $v$ do każdego z tych dwóch punktów.

Spójność własna

Ponieważ sferyczną geometrię eliptyczną można modelować jako, na przykład, sferyczną podprzestrzeń przestrzeni euklidesowej, wynika z tego, że jeśli geometria euklidesowa jest samospójna, to samo dotyczy sferycznej geometrii eliptycznej. Dlatego nie jest możliwe udowodnienie postulatu równoległości na podstawie pozostałych czterech postulatów geometrii euklidesowej.

Tarski udowodnił, że elementarna geometria euklidesowa jest zupełna : istnieje algorytm, który dla każdego zdania może wykazać, że jest ono prawdziwe lub fałszywe. (Nie narusza to twierdzenia Gödla , ponieważ geometria euklidesowa nie może opisać wystarczającej ilości arytmetyki , aby twierdzenie mogło zostać zastosowane). Wynika z tego, że elementarna geometria eliptyczna jest również samospójna i kompletna.

Zobacz też

Notatki

Alan F. Beardon, Geometria grup dyskretnych , Springer-Verlag, 1983
HSM Coxeter (1942) Non-Euclidean Geometry , rozdziały 5, 6 i 7: Geometria eliptyczna w 1, 2 i 3 wymiarach , University of Toronto Press , wznowione 1998 przez Mathematical Association of America , ISBN 0-88385-522-4 .
HSM Coxeter (1969) Wprowadzenie do geometrii , §6.9 Płaszczyzna eliptyczna, s. 92–95. John Wiley & Synowie .
„Geometria eliptyczna” , Encyklopedia matematyki , EMS Press , 2001 [1994]
Felix Klein (1871) „O tak zwanej geometrii nieeuklidesowej” Mathematische Annalen 4: 573–625, przetłumaczone i wprowadzone w John Stillwell (1996) Sources of Hyperbolic Geometry , American Mathematical Society ISBN 0-8218-0529-0 .
Boris Odehnal „O izotropowych kongruencjach prostych w eliptycznej trójprzestrzeni”
Eduard Study (1913) tłumacz DH Delphenich, „Podstawy i cele kinematyki analitycznej” , strona 20.
Alfred Tarski (1951) Metoda decyzyjna dla elementarnej algebry i geometrii . Uniw. prasy kalifornijskiej.
Franzén, Torkel (2005). Twierdzenie Gödla: niekompletny przewodnik po jego używaniu i nadużywaniu . AK Peters. ISBN 1-56881-238-8 .
Alfred North Whitehead (1898) Universal Algebra Archived 2014-09-03 at the Wayback Machine , Księga VI Rozdział 2: Geometria eliptyczna, s. 371–98.

Linki zewnętrzne

Media związane z geometrią eliptyczną w Wikimedia Commons