Podstawienie trygonometryczne

W matematyce podstawienie trygonometryczne to zastąpienie funkcji trygonometrycznych innymi wyrażeniami. W rachunku różniczkowym podstawienie trygonometryczne jest techniką obliczania całek. Ponadto tożsamości trygonometryczne można wykorzystać do uproszczenia pewnych całek zawierających wyrażenia pierwiastkowe . Podobnie jak w przypadku innych metod całkowania przez podstawienie, przy obliczaniu całki oznaczonej prostsze może być całkowite wydedukowanie funkcji pierwotnej przed zastosowaniem granic całkowania.

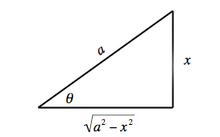
Przypadek I: Całki zawierające 2 ⁻ x ²

Niech ${\ Displaystyle x = a \ sin \ theta}$ i użyj tożsamości ${\ Displaystyle 1- \ sin ^ {2} \ theta = \ cos ^{2}\theta}$ .

Przykłady przypadku I

Konstrukcja geometryczna dla przypadku I

Przykład 1

W całce

${\ Displaystyle \ int {\ Frac {dx} {\ sqrt {a ^ {2} -x ^ {2}}}},}$

możemy użyć

${\ Displaystyle x = a \ sin \ theta, \ quad dx = a \ cos \ theta \, d \ theta, \ quad \ theta = \ arcsin {\ Frac {x} {a}}.}$

Następnie,

${\ Displaystyle {\ rozpocząć {wyrównane} \ int {\ Frac {dx} {\ sqrt {a ^ {2} -x ^ {2}}}} & = \ int {\ Frac {a \ cos \ theta \, d\theta}{\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}}\\[6pt]&=\int {\frac {a\cos \theta \, d\theta}{\sqrt {a^{2}(1-\sin ^{2}\theta )}}}\\[6pt]&=\int {\frac {a\cos \theta \,d\ theta }{\sqrt {a^{2}\cos ^{2}\theta }}}\\[6pt]&=\int d\theta \\[6pt]&=\theta +C\\[6pt] &=\arcsin {\frac {x}{a}}+C.\end{wyrównane}}}$

Powyższy krok wymaga, aby za $\ displaystyle a> 0}$ i ${\ displaystyle \ cos \ theta > 0}$ . Możemy wybrać $jako$$i$ pierwiastek nałożyć ograniczenie $\theta <\pi /2}$${\ Displaystyle - \ pi /$ przy użyciu odwrotnej funkcji sinusoidalnej.

W przypadku całki oznaczonej należy dowiedzieć się, jak zmieniają się granice całki. Na przykład, gdy $do$ od ${\ Displaystyle 0}$ za $\ Displaystyle a/2}$ , to ${\ Displaystyle \ sin \ theta}$ przechodzi od ${\ Displaystyle 0}$ do ${\ Displaystyle 1/2}$ , więc ${\ Displaystyle \ theta}$ przechodzi od ${\ Displaystyle 0}$ do ${\ Displaystyle \ pi / 6}$ . Następnie,

${\ Displaystyle \ int _ {0} ^ {a/2} {\ Frac {dx} {\ sqrt {a ^ {2} -x ^ {2}}}} = \ int _ {0} ^ {\ pi /6}d\theta ={\frac {\pi }{6}}.}$

Podczas wybierania granic wymagana jest pewna ostrożność. $-\pi /2<\theta <\pi /2$$powyższa$ integracja wymaga od displaystyle $0$$\pi /6$. Neglecting this restriction, one might have picked $\theta$ to go from $\pi$ to ${\ Displaystyle 5 \ pi / 6}$ , co spowodowałoby ujemną wartość rzeczywistą.

Alternatywnie, przed zastosowaniem warunków brzegowych należy w pełni oszacować całki nieoznaczone. W takim przypadku funkcja pierwotna daje

${\ Displaystyle \ int _ {0} ^ {a/2} {\ Frac {dx} {\ sqrt {a ^ {2} -x ^{2}}}}=\arcsin \left({\frac {x}{a}}\right){\Biggl |}_{0}^{a/2}=\arcsin \left({\frac {1}{2}}\right)-\arcsin(0)={\frac {\pi }{6}}}$ jak wcześniej.

Przykład 2

Całka

${\ Displaystyle \ int {\ sqrt {a ^ {2} -x ^ {2}}} \, dx,}$

można ocenić, pozwalając ${\ Displaystyle x = a \ sin \ theta \, dx = a \ cos \$

gdzie ${\ Displaystyle a> 0}$ tak, że ${\ Displaystyle {\ sqrt {a ^ {2}}} = a}$ i ${\ Displaystyle - {\ Frac {\ pi} {2}} \ leq \ theta \ leq {\ Frac {\ pi} {2}}}$ przez zakres łuku sinusoidalnego, tak że ${\ Displaystyle \ cos \ theta \ geq 0}$ i ${\ Displaystyle {\ sqrt {\ cos ^ {2} \ teta}} = \ cos \ teta}$ .

Następnie,

${\ Displaystyle {\ rozpocząć {wyrównane} \ int {\ sqrt {a ^ {2} -x ^ {2}}} \, dx & = \ int {\ sqrt {a ^ {2} -a ^ {2} \ sin ^{2}\theta }}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1-\sin ^{2} \theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(\cos ^{2}\theta )}}\ ,(a\cos \theta )\,d\theta \\[6pt]&=\int (a\cos \theta )(a\cos \theta )\,d\theta \\[6pt]&=a^ {2}\int \cos ^{2}\theta \,d\theta \\[6pt]&=a^{2}\int \left({\frac {1+\cos 2\theta}{2} }\right)\,d\theta \\[6pt]&={\frac {a^{2}}{2}}\left(\theta +{\frac {1}{2}}\sin 2\ theta \right)+C\\[6pt]&={\frac {a^{2}}{2}}(\theta +\sin \theta \cos \theta )+C\\[6pt]&={ \frac {a^{2}}{2}}\left(\arcsin {\frac {x}{a}}+{\frac {x}{a}}{\sqrt {1-{\frac {x ^{2}}{a^{2}}}}}\right)+C\\[6pt]&={\frac {a^{2}}{2}}\arcsin {\frac {x}{ a}}+{\frac {x}{2}}{\sqrt {a^{2}-x^{2}}}+C.\end{wyrównane}}}$

W przypadku całki oznaczonej granice zmieniają się po wykonaniu podstawienia i są określane za pomocą równania , z wartościami $za {\ Displaystyle \ theta = \ arcsin {\ Frac {x} {a}}}$ zakresu ${\ Displaystyle - {\ Frac {\ pi} {2}} \ równoważnik \ teta \ równoważnik {\ Frac {\ pi} {2}}}$ . Alternatywnie, zastosuj terminy brzegowe bezpośrednio do wzoru na funkcję pierwotną.

Na przykład całka oznaczona

${\ Displaystyle \ int _ {- 1} ^ {1} {\ sqrt {4-x ^ {2}}} \, dx,}$

można ocenić, zastępując ${\ Displaystyle x = 2 \ sin \ theta, \, dx = 2 \ cos \ theta \, d \ theta$ } granice określone za pomocą ${\ Displaystyle \ theta = \ arcsin {\ Frac {x} {2}}$ }

Ponieważ ${\ Displaystyle \ arcsin (1/2) = \ pi / 6}$ i ${\ Displaystyle \ arcsin (-1 /2)=-\pi /6}$ ,

${\ Displaystyle {\ rozpocząć {wyrównane} \ int _ {-1} ^ {1} {\ sqrt {4-x ^ {2}}} \, dx & = \ int _ {- \ pi / 6} ^ {\ pi /6}{\sqrt {4-4\sin ^{2}\theta }}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi / 6}^{\pi /6}{\sqrt {4(1-\sin ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\ int _{-\pi /6}^{\pi /6}{\sqrt {4(\cos ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[ 6pt]&=\int _{-\pi /6}^{\pi /6}(2\cos \theta )(2\cos \theta )\,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\cos ^{2}\theta \,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&=2\left[\theta +{\frac {1} {2}}\sin 2\theta \right]_{-\pi /6}^{\pi /6}=[2\theta +\sin 2\theta ]{\Biggl |}_{-\pi / 6}^{\pi /6}\\[6pt]&=\left({\frac {\pi }{3}}+\sin {\frac {\pi }{3}}\right)-\left (-{\frac {\pi }{3}}+\sin \left(-{\frac {\pi }{3}}\right)\right)={\frac {2\pi }{3}} +{\sqrt {3}}.\end{wyrównane}}}$

Z drugiej strony bezpośrednie zastosowanie członów brzegowych do otrzymanego wcześniej wzoru na wydajności pierwotne

${\ Displaystyle {\ rozpocząć {wyrównane} \ int _ {-1} ^ {1} {\ sqrt {4-x ^ {2}}} \, dx & = \ lewo [{\ Frac {2 ^ {2}} {2}}\arcsin {\frac {x}{2}}+{\frac {x}{2}}{\sqrt {2^{2}-x^{2}}}\right]_{- 1}^{1}\\[6pt]&=\left(2\arcsin {\frac {1}{2}}+{\frac {1}{2}}{\sqrt {4-1}}\ right)-\left(2\arcsin \left(-{\frac {1}{2}}\right)+{\frac {-1}{2}}{\sqrt {4-1}}\right) \\[6pt]&=\left(2\cdot {\frac {\pi }{6}}+{\frac {\sqrt {3}}{2}}\right)-\left(2\cdot \ left(-{\frac {\pi }{6}}\right)-{\frac {\sqrt {3}}{2}}\right)\\[6pt]&={\frac {2\pi} {3}}+{\sqrt {3}}\end{wyrównane}}}$

jak wcześniej.

Przypadek II: Całki zawierające 2 ⁺ x ²

Niech ${\ Displaystyle x = a \ tan \ theta}$ i użyj tożsamości ${\ Displaystyle 1 + \ tan ^ {2} \ theta = \ sec ^{2}\theta}$ .

Przykłady przypadku II

Konstrukcja geometryczna dla przypadku II

Przykład 1

W całce

${\ Displaystyle \ int {\ Frac {dx} {a ^ {2} + x ^ {2}}}}$

możemy napisać

${\ Displaystyle x = a \ tan \ teta \ quad dx = a \ sek ^ {2} \ teta \ ,d\theta ,\quad \theta =\arctan {\frac {x}{a}},}$

tak, że całka staje się

${\ Displaystyle {\ rozpocząć {wyrównane} \ int {\ Frac {dx} {a ^ {2} + x ^ {2}}} & = \ int {\ Frac {a \ s ^ {2} \ teta \, d\theta }{a^{2}+a^{2}\tan ^{2}\theta }}\\[6pt]&=\int {\frac {a\s ^{2}\theta \, d\theta }{a^{2}(1+\tan ^{2}\theta )}}\\[6pt]&=\int {\frac {a\sec ^{2}\theta \,d\ theta }{a^{2}\sec ^{2}\theta }}\\[6pt]&=\int {\frac {d\theta }{a}}\\[6pt]&={\frac { \theta }{a}}+C\\[6pt]&={\frac {1}{a}}\arctan {\frac {x}{a}}+C,\end{wyrównane}}}$

pod warunkiem, ${\ Displaystyle a \ neq 0}$ .

W przypadku całki oznaczonej granice zmieniają się po wykonaniu podstawienia i są określane za pomocą równania , z wartościami z zakresu $Frac {x} {a}}}$${\ Displaystyle - {\ Frac {\ pi} {2}} <\ teta <{\ Frac {\ pi} {2}}}$ . Alternatywnie, zastosuj terminy brzegowe bezpośrednio do wzoru na funkcję pierwotną.

Na przykład całka oznaczona

${\ Displaystyle \ int _ {0} ^ {1} {\ Frac {4 \, dx} {1 + x ^ {2}}} \,}$

${\ Displaystyle x = \ tan \ theta, \, dx = \ sec ^ {2} \ theta \, d \$ dębnik } granice określone za pomocą ${\ Displaystyle \ theta = \ arctan x}$ .

Ponieważ ${\ Displaystyle \ arctan 0 = 0}$ i ${\ Displaystyle \ arctan 1 = \ pi / 4}$ ,

${\ Displaystyle {\ rozpocząć {wyrównane} \ int _ {0} ^ {1} {\ Frac {4 \, dx} 1 + x ^ {2}}} i = 4 \ int _ {0} ^ {1 }{\frac {dx}{1+x^{2}}}\\[6pt]&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{1+\tan ^{2}\theta }}\\[6pt]&=4\int _{0}^{\pi /4}{\frac {\s ^{2} \theta \,d\theta }{\sec ^{2}\theta }}\\[6pt]&=4\int _{0}^{\pi /4}d\theta \\[6pt]&= (4\theta ){\Bigg |}_{0}^{\pi /4}=4\left({\frac {\pi}}{4}}-0\right)=\pi .\end{wyrównane }}}$

Tymczasem bezpośrednie zastosowanie członów brzegowych do wzoru na wydajności pierwotne

${\ Displaystyle {\ rozpocząć {wyrównane} \ int _ {0} ^ {1} {\ Frac {4 \, dx} {1 + x ^ {2}}} \, & = 4 \int _{0}^{1}{\frac {dx}{1+x^{2}}}\\&=4\left[{\frac {1}{1}}\arctan {\frac { x}{1}}\right]_{0}^{1}\\&=4(\arctan x){\Bigg |}_{0}^{1}\\&=4(\arctan 1- \arctan 0)\\&=4\left({\frac {\pi }{4}}-0\right)=\pi ,\end{wyrównane}}}$

tak samo jak ostatnio.

Przykład 2

Całka

${\ Displaystyle \ int {\ sqrt {a ^ {2} + x ^ {2}}} \, {dx}}$

można ocenić, pozwalając ${\ Displaystyle x = a \ tan \ theta, \, dx = a \ sec ^ { 2}\theta \,d\theta ,\,\theta =\arctan {\frac {x}{a}},}$

gdzie za $\ Displaystyle a> 0}$ tak, że ${\ Displaystyle {\ sqrt {a ^ {2}}} = a}$ i ${\ Displaystyle - {\ Frac {\ pi} {2}}<\ theta <{\ Frac {\ pi} {2}}}$ przez zakres arcus tangens, tak że ${\ Displaystyle \ sec \ theta > 0}$ i ${\ Displaystyle {\ sqrt {\ sec ^ {2} \ theta}} = \ sec \ theta}$ .

Następnie,

${\ Displaystyle {\ rozpocząć {wyrównane} \ int {\ sqrt {a ^ {2} + x ^ {2}}} \, dx & = \ int {\ sqrt {a ^ {2} + a ^ {2} \ tan ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1+\tan ^{2}\theta )}}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}\sec ^{2 }\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int (a\sec \theta )(a\sec ^{2}\theta ) \,d\theta \\[6pt]&=a^{2}\int \sec ^{3}\theta \,d\theta .\\[6pt]\end{aligned}}}$

Całkę siecznej sześcianu można obliczyć za pomocą całkowania przez części . W rezultacie,

${\ Displaystyle {\ rozpocząć {wyrównane} \ int {\ sqrt {a ^ {2} + x ^ {2}}} \, dx & = {\ Frac {a ^ {2}} {2}} (\ s \ theta \tan \theta +\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\sqrt { 1+{\frac {x^{2}}{a^{2}}}}}\cdot {\frac {x}{a}}+\ln \left|{\sqrt {1+{\frac { x^{2}}{a^{2}}}}}+{\frac {x}{a}}\right|\right)+C\\[6pt]&={\frac {1}{2 }}\left(x{\sqrt {a^{2}+x^{2}}}+a^{2}\ln \left|{\frac {x+{\sqrt {a^{2}+x ^{2}}}}{a}}\prawo|\prawo)+C.\end{wyrównane}}}$

Przypadek III: Całki zawierające x ² − a ²

Niech ${\ Displaystyle x = a \ sec \ theta}$ i użyj tożsamości ${\ Displaystyle \ sec ^ {2} \ teta -1 = \ tan ^ {2} \ teta.}$

Przykłady przypadku III

Konstrukcja geometryczna dla przypadku III

Całki jak

${\ Displaystyle \ int {\ Frac {dx} {x ^ {2} -a ^ {2}}}}$

można również ocenić za pomocą ułamków cząstkowych , a nie podstawień trygonometrycznych. Jednak całka

${\ Displaystyle \ int {\ sqrt {x ^ {2} -a ^ {2}}} \, dx}$

Nie mogę. W takim przypadku odpowiednim zamiennikiem jest:

$\ Displaystyle x = a \ sec \ theta \, dx = a \ sec \ theta \ tan \ theta \,d\theta ,\,\theta =\operatorname {arcsec} {\frac {x}{a}},}$

gdzie za $\ Displaystyle a> 0}$ tak, że ${\ displaystyle {\ sqrt {a ^ {2}}} = a}$ i ${\ Displaystyle 0 \ równoważnik \ theta <{{ \ frac {\ pi} {2}}}$ zakładając , że i $tan \ theta \ geq 0$$\ Displaystyle$${\ Displaystyle {\ sqrt {\ dębnik ^ {2} \ teta}} = \ tan \ teta}$ .

Następnie,

${\ Displaystyle {\ rozpocząć {wyrównane} \ int {\ sqrt {x ^ {2} -a ^ {2}}} \, dx & = \ int {\ sqrt {a ^ {2} \ s ^ {2} \ theta -a^{2}}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}(\sec ^{2}\theta - 1)}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}\tan ^{2}\theta }}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int a^{2}\sec \theta \tan ^{2}\theta \,d\theta \\&=a^{2}\int (\sec \theta )(\sec ^{2}\theta -1)\,d\theta \\&=a^{2}\int (\sec ^{3}\theta -\sec \theta )\ ,d\theta .\end{wyrównane}}}$

funkcji siecznej można obliczyć , mnożąc licznik i mianownik przez ${\ Displaystyle (\ sec \ theta + \ tan \ theta)}$ i całkę siecznej podzieloną na części. W rezultacie,

${\ Displaystyle {\ rozpocząć {wyrównane} \ int {\ sqrt {x ^ {2} -a ^ {2}}} \, dx & = {\ Frac {a ^ {2}} {2}} (\ s \ theta \tan \theta +\ln |\sec \theta +\tan \theta |)-a^{2}\ln |\sec \theta +\tan \theta |+C\\[6pt]&={\ frac {a^{2}}{2}}(\sec \theta \tan \theta -\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a ^{2}}{2}}\left({\frac {x}{a}}\cdot {\sqrt {{\frac {x^{2}}{a^{2}}}-1}} -\ln \left|{\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}\right|\right)+ C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {x^{2}-a^{2}}}-a^{2}\ln \left| {\frac {x+{\sqrt {x^{2}-a^{2}}}}{a}}\right|\right)+C.\end{aligned}}}$

π ${\ Displaystyle {\ Frac {\ pi} {2}} <\ theta \ równoważnik \ pi}$ , co dzieje się, gdy $\ Displaystyle x <0}$ biorąc pod uwagę zakres arcsecans, $tego$ _ $_$ _ ta walizka.

Podstawienia eliminujące funkcje trygonometryczne

Podstawiania można użyć do usunięcia funkcji trygonometrycznych.

Na przykład,

${\ Displaystyle {\ rozpocząć {wyrównane} \ int f (\ sin (x), \ cos (x)} \, dx & = \ int {\ Frac {1} {\ pm {\ sqrt {1-u ^ {2 }}}}}f\left(u,\pm {\sqrt {1-u^{2}}}\right)\,du&&u=\sin(x)\\[6pt]\int f(\sin( x),\cos(x))\,dx&=\int {\frac {1}{\mp {\sqrt {1-u^{2}}}}}f\left(\pm {\sqrt {1 -u^{2}}},u\right)\,du&&u=\cos(x)\\[6pt]\int f(\sin(x),\cos(x))\,dx&=\int { \frac {2}{1+u^{2}}}f\left({\frac {2u}{1+u^{2}}},{\frac {1-u^{2}}{1 +u^{2}}}\right)\,du&&u=\tan \left({\tfrac {x}{2}}\right)\\[6pt]\end{aligned}}}$

Ostatnie podstawienie jest znane jako podstawienie Weierstrassa , które wykorzystuje wzory stycznych półkątów .

Na przykład,

${\ Displaystyle {\ rozpocząć {wyrównane} \ int {\ Frac {4 \ cos x} {(1 + \ cos x) ^ {3}}} \, dx & = \ int {\ Frac {2} {1 + u ^{2}}}{\frac {4\left({\frac {1-u^{2}}{1+u^{2}}}\right)}{\left(1+{\frac { 1-u^{2}}{1+u^{2}}}\right)^{3}}}\,du=\int (1-u^{2})(1+u^{2} )\,du\\&=\int (1-u^{4})\,du=u-{\frac {u^{5}}{5}}+C=\tan {\frac {x} {2}}-{\frac {1}{5}}\tan ^{5}{\frac {x}{2}}+C.\end{wyrównane}}}$

Podstawienie hiperboliczne

Podstawienia funkcji hiperbolicznych można również wykorzystać do uproszczenia całek.

$_$ całce _ ${\ Displaystyle x = a \ sinh {u}}$ , ${\ displaystyle dx = a \ cosh u \ du.}$

Następnie, używając tożsamości ${\ Displaystyle \ cosh ^ {2} (x) - \ sinh ^ {2} (x) = 1}$ i ${\ Displaystyle \ sinh ^ {-1} {x} = \ ln (x + {\ sqrt {x ^ {2} + 1}}),}$

${\ Displaystyle {\ rozpocząć {wyrównane} \ int {\ Frac {dx} {\ sqrt {a ^ {2} + x ^ {2}}}} \, & = \ int {\ Frac {a \ cosh u \ ,du}{\sqrt {a^{2}+a^{2}\sinh ^{2}u}}}\ ,\\[6pt]&=\int {\frac {a\cosh {u}\ ,du}{a{\sqrt {1+\sinh ^{2}{u}}}}}\,\\[6pt]&=\int {\frac {a\cosh {u}}{a\cosh u}}\,du\\[6pt]&=u+C\\[6pt]&=\sinh ^{-1}{\frac {x}{a}}+C\\[6pt]&=\ ln \left({\sqrt {{\frac {x^{2}}{a^{2}}}+1}}+{\frac {x}{a}}\right)+C\\[6pt ]&=\ln \left({\frac {{\sqrt {x^{2}+a^{2}}}+x}{a}}\right)+C\end{wyrównane}}}$

Zobacz też

• Całkowanie przez podstawienie
• podstawienie Weierstrassa
• podstawienie Eulera