Slerp

W grafice komputerowej Slerp jest skrótem od sferycznej interpolacji liniowej , wprowadzonej przez Kena Shoemake'a w kontekście interpolacji kwaternionów w celu animacji obrotu 3D . Odnosi się do ruchu ze stałą prędkością wzdłuż łuku wielkiego koła o promieniu jednostkowym , przy danych końcach i parametrze interpolacji z zakresu od 0 do 1.

Geometryczne Slerp

₀ Slerp ma wzór geometryczny niezależny od kwaternionów i niezależny od wymiaru przestrzeni, w której zanurzony jest łuk. Wzór ten, symetryczna suma ważona przypisana Glennowi Davisowi, opiera się na fakcie, że dowolny punkt krzywej musi być liniową kombinacją końców. Niech p i p ₁ będą pierwszym i ostatnim punktem łuku, a t parametrem 0 ≤ t ≤ 1. Oblicz Ω jako kąt oparty na łuku, tak że ₀ cos Ω = p ∙ p ₁ , n -wymiarowy iloczyn skalarny wektorów jednostkowych od początku do końca. Wzór geometryczny jest wtedy

{\ Displaystyle \ operatorname {Slerp} (p_ {0}, p_ {1}; t) = {\ Frac {\ sin {[(1-t) \ Omega}]} {\ sin \ Omega}} p_ {0 }+{\frac {\sin[t\Omega ]}{\sin \Omega }}p_{1}.}

Symetria polega na tym, że ${\ displaystyle \ operatorname {Slerp} (p_ {0}, p_ {1}; t)}$ ${\ Displaystyle = \ operatorname {Slerp} (p_ {1}, p_ {0}; 1-t)}$ . W granicy Ω → 0 wzór ten sprowadza się do odpowiedniego wzoru symetrycznego dla interpolacji liniowej ,

{\ Displaystyle \ operatorname {Lerp} (p_ {0}, p_ {1}; t) = (1-t) p_ {0} + tp_ {1}. \, \!}

Ścieżka Slerpa jest w rzeczywistości odpowiednikiem geometrii sferycznej ścieżki wzdłuż odcinka linii w płaszczyźnie; koło wielkie jest sferycznym obiektem geodezyjnym .

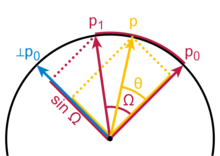
Wektor ukośny jest prostowany do współczynnika Slerpa.

Bardziej znany niż ogólny wzór Slerpa jest przypadek, gdy wektory końcowe są prostopadłe, w którym to przypadku wzór ma postać ₀ p cos θ + p ₁ sin θ . Zakładając θ = t $π$ /2 i stosując tożsamość trygonometryczną cos θ = sin ( $π$ /2 - θ ) , otrzymujemy wzór Slerpa. Współczynnik 1/sin Ω we wzorze ogólnym jest normalizacją, ponieważ wektor p ₁₀₀ pod kątem Ω do p rzutuje na prostopadłą ⊥ p o długości tylko sin Ω .

₀ Niektóre szczególne przypadki Slerpa dopuszczają bardziej wydajne obliczenia. Kiedy na obraz rastrowy ma zostać narysowany łuk kołowy, preferowaną metodą jest pewna odmiana algorytmu okręgu Bresenhama . Ocena przy specjalnych wartościach parametrów 0 i 1 w prosty sposób daje p i p ₁ ; i bisekcja, ocena przy ½, upraszcza do ₀ ( p + p ₁ )/2 , znormalizowana. Innym szczególnym przypadkiem, powszechnym w animacji, jest ocena ze stałymi końcami i równymi krokami parametrycznymi. Jeśli p.k _{_ −1} i p _k to dwie kolejne wartości i jeśli c jest dwukrotnością ich iloczynu skalarnego (stała dla wszystkich kroków), to następna wartość, p _{k +1} , jest odbiciem p _{k +1} = do p _k − p _{k − 1} .

Kwaternion Slerp

Kiedy Slerp jest zastosowany do kwaternionów jednostkowych , ścieżka kwaternionów jest odwzorowywana na ścieżkę poprzez rotacje 3D w standardowy sposób . Efektem jest obrót ze stałą prędkością kątową wokół ustalonej osi obrotu . Gdy początkowym punktem końcowym jest kwaternion tożsamościowy, Slerp daje segment jednoparametrowej podgrupy zarówno grupy Liego rotacji 3D, SO(3) , jak i jej uniwersalnej grupy obejmującej kwaternionów jednostkowych, S ³ . Slerp wyznacza najprostszą i najkrótszą ścieżkę między punktami końcowymi kwaternionów i odwzorowuje obrót o kąt 2 Ω. Jednakże, ponieważ pokrycie jest podwójne ( q i - q odwzorowują ten sam obrót), ścieżka obrotu może skręcić albo w „krótką drogę” (mniej niż 180 °), albo w „długą drogę” (więcej niż 180 °). Długim ścieżkom można zapobiec, negując jeden koniec, jeśli iloczyn skalarny, cos Ω , jest ujemny, zapewniając w ten sposób, że -90° ≤ Ω ≤ 90°.

Slerp ma również wyrażenia w kategoriach algebry kwaternionów, wszystkie używające potęgowania . Potęgi rzeczywiste kwaternionów definiuje się za pomocą funkcji wykładniczej kwaternionu , zapisanej jako e ^q i danej przez szereg potęgowy , równie znany z rachunku różniczkowego, analizy zespolonej i algebry macierzy:

{\ Displaystyle e ^ {q} = 1 + q + {\ Frac {q ^ {2}} {2}} + {\ Frac {q ^ {3}} {6}} + \ cdots + {\ Frac {q ^{n}}{n!}}+\cdots .}

Zapisując kwaternion jednostkowy q w postaci wersora , cos Ω + v sin Ω , z v jednostkowym 3-wektorem i zauważając, że kwadrat kwaternionu v ² równa się -1 (co oznacza kwaternionową wersję wzoru Eulera ), mamy e ^{v Ω} = q i q ^t = cos t Ω + v sin t Ω . Identyfikacja zainteresowania to q = q ₀₁ q ⁻¹ , tak że część rzeczywista q to cos Ω , taki sam jak iloczyn skalarny geometryczny użyty powyżej. Oto cztery równoważne wyrażenia kwaternionów dla Slerpa.

{\ Displaystyle {\ początek {wyrównane} \ nazwa operatora {Slerp} (q_ {0}, q_ {1}, t) i = q_ {0} (q_ {0} ^ {-1} q_ {1} )^{t}\\[6pt]&=q_{1}(q_{1}^{-1}q_{0})^{1-t}\\[6pt]&=(q_{0}q_ {1}^{-1})^{1-t}q_{1}\\[6pt]&=(q_{1}q_{0}^{-1})^{t}q_{0}\ koniec{wyrównany}}}

₀ Pochodna Slerp ₀ ( q , q ₁ ; t ) względem t , zakładając, że końce są stałe, to log( ^{q 1 q −1} ) _razy wartość funkcji , gdzie logarytm naturalny kwaternionu w tym przypadku daje połowę kąta 3D wektor prędkości . Początkowy wektor styczny jest przenoszony równolegle do każdej stycznej wzdłuż krzywej; zatem krzywa jest rzeczywiście geodezyjna.

W przestrzeni stycznej w dowolnym punkcie krzywej kwaternionu Slerpa odwrotność mapy wykładniczej przekształca krzywą w odcinek linii. Krzywe Slerpa nieprzechodzące przez punkt nie przekształcają się w linie w przestrzeni stycznej tego punktu.

Quaternion Slerps są powszechnie używane do konstruowania gładkich krzywych animacji poprzez naśladowanie konstrukcji afinicznych, takich jak algorytm de Casteljau dla krzywych Béziera . Ponieważ kula nie jest przestrzenią afiniczną , znane właściwości konstrukcji afinicznych mogą zawieść, chociaż w przeciwnym razie skonstruowane krzywe mogą być całkowicie zadowalające. Na przykład algorytm de Casteljau może zostać użyty do podziału krzywej w przestrzeni afinicznej; to nie działa na kuli.

Dwuwartościowy Slerp można rozszerzyć w celu interpolacji między wieloma kwaternionami jednostkowymi, ale rozszerzenie traci ustalony czas wykonania algorytmu Slerp.

Zobacz też

Linki zewnętrzne

Szewc, Ken. „Animowanie obrotu za pomocą krzywych kwaternionów” (PDF) . SIGGRAPH 1985. {{ cite web }} : CS1 maint: status url ( link )
Erik B., Dam; Martin, Koch; Lillholm, Martin (17 lipca 1998). „Kwaterniony, interpolacja i animacja” (PDF) . Uniwersytet w Kopenhadze. Zarchiwizowane (PDF) od oryginału w dniu 30.08.2017 r.
Cios, Jonathan (26 lutego 2004). „Zrozumieć Slerp, a potem go nie używać” . Zarchiwizowane od oryginału w dniu 25.08.2017 r.
Martin, Brian (23 czerwca 1999). „Brian Martin o animacji Quaternion” . Zarchiwizowane od oryginału w dniu 24.03.2016 r.