Przestrzeń afiniczna

Nie należy mylić z przestrzenią powinowactwa .

W ${\ Displaystyle \ mathbb {R} ^ {3},}$$Displaystyle$$\ mathbf {0} \notin P_{2}}$ (na niebiesko) nie jest podprzestrzenią wektorową, ponieważ i ${\ Displaystyle \ mathbf {a} + \ mathbf {b} \ notin P_ {2};}$ jest to podprzestrzeń afiniczna . Jego kierunek (podprzestrzeń liniowa $tą$ podprzestrzenią afiniczną) to dolna (zielona) płaszczyzna, podprzestrzenią wektorową. Chociaż i są w $P_ {2},}$$2$ { $\ Displaystyle$ ich różnica jest , który nie należy ${\ Displaystyle P_ {2},}$ ale należy do przestrzeni wektorowej ${\ displaystyle P_ {1}.}$

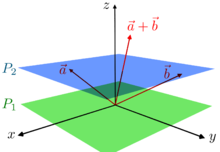
W matematyce przestrzeń afiniczna jest strukturą geometryczną , która uogólnia niektóre właściwości przestrzeni euklidesowych w taki sposób, że są one niezależne od pojęć odległości i miary kątów, zachowując jedynie właściwości związane z równoległością i stosunkiem długości równoległości segmenty linii .

W przestrzeni afinicznej nie ma wyróżnionego punktu, który służy jako początek. Dlatego żaden wektor nie ma ustalonego początku i żaden wektor nie może być jednoznacznie powiązany z punktem. Zamiast tego w przestrzeni afinicznej istnieją wektory przemieszczenia , zwane także wektorami translacji lub po prostu translacjami , między dwoma punktami przestrzeni. Zatem ma sens odejmowanie dwóch punktów przestrzeni, dając wektor translacji, ale nie ma sensu dodawać dwóch punktów przestrzeni. Podobnie sensowne jest dodanie wektora przemieszczenia do punktu przestrzeni afinicznej, co spowoduje powstanie nowego punktu przesuniętego od punktu początkowego o ten wektor.

Dowolną przestrzeń wektorową można postrzegać jako przestrzeń afiniczną; sprowadza się to do zapomnienia o szczególnej roli, jaką odgrywa wektor zerowy . W tym przypadku elementy przestrzeni wektorowej można postrzegać albo jako punkty przestrzeni afinicznej, albo jako wektory przemieszczeń lub translacje . Gdy jest traktowany jako punkt, wektor zerowy nazywany jest początkiem . Dodanie ustalonego wektora do elementów podprzestrzeni liniowej (podprzestrzeni wektorowej) przestrzeni wektorowej tworzy podprzestrzeń afiniczną . Powszechnie mówi się, że ta podprzestrzeń afiniczna została uzyskana przez translację (od początku) podprzestrzeni liniowej przez wektor translacji (wektor dodany do wszystkich elementów przestrzeni liniowej). W skończonych wymiarach taka podprzestrzeń afiniczna jest zbiorem rozwiązań niejednorodnego układu liniowego. Wektory przemieszczenia dla tej przestrzeni afinicznej są rozwiązaniami odpowiedniego jednorodnego układu liniowego, który jest podprzestrzenią liniową. Natomiast podprzestrzenie liniowe zawsze zawierają początek przestrzeni wektorowej.

Wymiar przestrzeni afinicznej definiuje się jako wymiar przestrzeni wektorowej jej translacji. Przestrzeń afiniczna o wymiarze jeden jest linią afiniczną . Przestrzeń afiniczna o wymiarze 2 jest płaszczyzną afiniczną . Podprzestrzeń afiniczna o wymiarze n – 1 w przestrzeni afinicznej lub przestrzeni wektorowej o wymiarze n jest hiperpłaszczyzną afiniczną .

Nieformalny opis

Geneza z perspektywy Alicji i Boba. Obliczenia wektorowe z perspektywy Alicji są zaznaczone na czerwono, podczas gdy obliczenia Boba na niebiesko.

Następująca charakterystyka może być łatwiejsza do zrozumienia niż zwykła definicja formalna: przestrzeń afiniczna to to, co pozostaje z przestrzeni wektorowej po zapomnieniu, który punkt jest początkiem (lub, używając słów francuskiego matematyka Marcela Bergera , „Przestrzeń afiniczna przestrzeń to nic innego jak przestrzeń wektorowa, o której pochodzeniu próbujemy zapomnieć, dodając translacje do map liniowych”). Wyobraź sobie, że Alicja wie, że dany punkt jest faktycznym początkiem, ale Bob uważa, że ​​inny punkt — nazwij go p — jest początkiem. Należy dodać dwa wektory a i b . Bob rysuje strzałkę od punktu p do punktu a i kolejną strzałkę od punktu p do punktu b i uzupełnia równoległobok, aby znaleźć to, co Bob uważa za a + b , ale Alicja wie, że tak naprawdę obliczył

p + ( za - p ) + ( b - p ) .

Podobnie Alicja i Bob mogą oszacować dowolną kombinację liniową aib lub dowolnego skończonego zbioru wektorów i generalnie otrzymają różne odpowiedzi . Jeśli jednak suma współczynników w kombinacji liniowej wynosi 1, to Alicja i Bob dojdą do tej samej odpowiedzi.

Jeśli Alice podróżuje do

λ za + (1 - λ) b

wtedy Bob może podobnie podróżować

p + λ( za - p ) + (1 - λ)( b - p ) = λ za + (1 - λ) b .

W tych warunkach, dla wszystkich współczynników λ + (1 − λ) = 1 , Alicja i Bob opisują ten sam punkt tą samą kombinacją liniową, mimo że używają różnych początków.

Podczas gdy tylko Alicja zna „strukturę liniową”, zarówno Alicja, jak i Bob znają „strukturę afiniczną” — tj. wartości kombinacji afinicznych , zdefiniowanych jako kombinacje liniowe, w których suma współczynników wynosi 1. Zbiór o strukturze afinicznej jest przestrzeń afiniczna.

Definicja

Przestrzeń afiniczna to zbiór A wraz z $\ displaystyle {\ overrightarrow$ wektorową przechodnią i swobodną akcją grupy addytywnej ZA $A}}}$ na planie A. Elementy przestrzeni afinicznej A nazywane są punktami . Mówi $wektorami$ przestrzeń wektorowa jest powiązana z przestrzenią afiniczną, a jej elementy nazywane są , translacjami lub czasami wektorami .

Wyraźnie powyższa definicja oznacza, że ​​akcja jest odwzorowaniem, ogólnie oznaczanym jako dodatek,

${\ Displaystyle {\ rozpocząć {wyrównane} A \ razy {\ overrightarrow {A}} &\ do A \\ (a, v) \; &\ mapsto a+v,\end{wyrównane}}}$

który ma następujące właściwości.

1. Właściwa tożsamość:

   0${\ Displaystyle \ forall a \ in A, \; a + 0 = a}$ , gdzie jest wektor zerowy w ${\ Displaystyle {\ overrightarrow {A}}}$

2. Łączność:

   ${\ Displaystyle \ forall v, w \ in {\ overrightarrow {A}} \ forall a \ in A, \; (a + v) + w = ​​a + (v + w)}$ (tutaj ostatni + jest dodatkiem w ${\ Displaystyle {\ overrightarrow {A}}}$ )

3. dla każdego $za$${\ Displaystyle {\ overrightarrow {A}} \ do A \ okrężnica v$ + jest bijekcją .

   przechodnia:

Pierwsze dwie właściwości po prostu definiują właściwości (prawej) akcji grupowej. Trzecia właściwość charakteryzuje czynności swobodne i przechodnie, przy czym charakter on pochodzi od przechodniości, a następnie charakter injektywny wynika z tego, że czynność jest swobodna. Istnieje czwarta właściwość, która wynika z 1, 2 powyżej:

4. tłumaczeń jeden do jednego

Dla wszystkich ${\ Displaystyle v \ w {\ overrightarrow {A}}}$ odwzorowanie ${\ Displaystyle A \ do A \ dwukropek a \ mapsto a + v}$ jest bijekcja.

Właściwość 3 jest często używana w następującej równoważnej formie (5. właściwość).

5. Odejmowanie:

Dla każdego za , b w ZA , istnieje unikalny $oznaczony$ b - za , taki, że ${\ displaystyle b = a + v}$ .

Innym sposobem wyrażenia definicji jest to, że przestrzeń afiniczna jest główną jednorodną przestrzenią działania grupy addytywnej przestrzeni wektorowej. Przestrzenie jednorodne są z definicji wyposażone w przechodnie działanie grupowe, a dla głównej przestrzeni jednorodnej takie działanie przechodnie jest z definicji wolne.

Odejmowanie i aksjomaty Weyla

$.$ na zdefiniowanie odejmowania dla dowolnej uporządkowanej pary ( b , a ) punktów w A , tworząc wektor Ten wektor, oznaczony jako ${\ displaystyle ba}$ lub ${\ displaystyle {\ overrightarrow {ab}}}$ jest definiowany jako unikalny wektor w takim ${\ displaystyle {\ overrightarrow {A}}}$ To

${\ displaystyle a + (ba) = b.}$

Istnienie wynika z przechodniości działania, a wyjątkowość wynika z tego, że działanie jest wolne.

To odejmowanie ma dwie następujące właściwości, zwane aksjomatami Weyla :

1. ${\ Displaystyle \ forall a \ w A, \; \ forall v \ in {\ overrightarrow {A}}}$ , istnieje unikalny punkt ${\ Displaystyle b \ w A}$ takie, że ${\ displaystyle ba = v.}$
2. ${\ Displaystyle \ forall a, b, c \ w A, \; (cb) + (ba) = ok.}$

W geometrii euklidesowej drugi z aksjomatów Weyla jest powszechnie nazywany regułą równoległoboku .

$równoważnie$ zdefiniować jako zbiór punktów A wraz z przestrzenią wektorową i odejmowaniem spełniającym aksjomaty Weyla W tym przypadku dodanie wektora do punktu jest zdefiniowane na podstawie pierwszego z aksjomatów Weyla.

Podprzestrzenie afiniczne i równoległość

Podprzestrzeń afiniczna (zwana także w niektórych kontekstach rozmaitością liniową , płaską lub, w stosunku do liczb rzeczywistych , rozmaitością liniową ) B przestrzeni afinicznej A jest podzbiorem A takim, że dany punkt ${ \ Displaystyle a \ in B}$ , zbiór wektorów ${\ Displaystyle {\ overrightarrow {B}} = \ {ba \ mid b \ in B \}}$ jest liniowy podprzestrzeń z ${\ displaystyle {\ overrightarrow {A}}}$ . Ta właściwość, która nie zależy od wyboru a , implikuje, że $B$ jest przestrzenią afiniczną, z którą jest przestrzeń wektorowa

Podprzestrzenie afiniczne A są podzbiorami A postaci

${\ Displaystyle a + V = \ {a + w: w \ w V \},}$

gdzie a jest punktem ZA , a V jest liniową podprzestrzenią ${\ displaystyle {\ overrightarrow {A}}}$ .

Liniowa podprzestrzeń powiązana z podprzestrzenią afiniczną jest często nazywana jej kierunkiem , a dwie podprzestrzenie, które mają ten sam kierunek, nazywane są równoległymi .

Implikuje to następujące uogólnienie aksjomatu Playfaira : Mając dany kierunek V , dla dowolnego punktu a z A istnieje jedna i tylko jedna podprzestrzeń afiniczna o kierunku V , która przechodzi przez a , a mianowicie podprzestrzeń a + V .

Każde tłumaczenie ${\ Displaystyle A \ do A: a \ mapsto a + v}$ odwzorowuje dowolną podprzestrzeń afiniczną na podprzestrzeń równoległą.

Termin równoległy jest również używany w odniesieniu do dwóch podprzestrzeni afinicznych, tak że kierunek jednej jest zawarty w kierunku drugiej.

Mapa afiniczna

Biorąc pod uwagę dwie przestrzenie afiniczne A i B , z którymi powiązane przestrzenie wektorowe to $\ overrightarrow {B}}}$ → $displaystyle {$ , mapa afiniczna lub homomorfizm od A do B jest mapą

${\ Displaystyle f: A \ do B}$

takie że

${\ Displaystyle {\ rozpocząć {wyrównane} {\ overrightarrow {f}}: {\ overrightarrow {A}} i \ do {\ overrightarrow {B}}\\ba&\mapsto f(b)-f(a)\end{wyrównane}}}$

jest dobrze zdefiniowaną mapą liniową. Przez $zdefiniowanie$ rozumie się, że za - za = re - do implikuje fa ( b ) - fa ( ) = fa ( re ) - fa ( do ) .

Oznacza $Displaystyle v \ in {\ overrightarrow {A}$ , że dla punktu i wektora $\$

${\ Displaystyle f (a + v) = f (a) + {\ overrightarrow {f}} (v).}$

Dlatego, ponieważ dla dowolnego danego b w A , b = a + v dla unikalnego v , f jest całkowicie określone przez jego wartość w jednym punkcie i powiązaną mapę liniową ${\ displaystyle {\ overrightarrow {f}}}$ .

Endomorfizmy

Główne artykuły: transformacja afiniczna i grupa afiniczna

Transformacja afiniczna lub endomorfizm przestrzeni afinicznej $.$ mapą afiniczną z tej przestrzeni do samej siebie Jedną ważną rodziną przykładów są tłumaczenia: biorąc pod uwagę wektor $,$ mapa translacji $A}$$}: A \$$afiniczną$ , który wysyła $}$$}$ dla każdego jest mapą Inną ważną rodziną przykładów są mapy liniowe wyśrodkowane na początku: biorąc pod uwagę punkt $,$ mapę liniową można zdefiniować mapę afiniczną $} styl wyświetlania L_{M,b}:A\rightarrow A}$${\ Displaystyle M$ wg

$${\ Displaystyle L_ {M, b} (a) = b + M (ab)}$$

dla każdego ${\ displaystyle a}$ w ${\ displaystyle A}$ .

Po dokonaniu wyboru pochodzenia $b$ każda mapa afiniczna może zostać zapisana w unikalny sposób jako połączenie tłumaczenia i mapy liniowej wyśrodkowanej w $\ displaystyle b}$ .

Przestrzenie wektorowe jako przestrzenie afiniczne

Każdą przestrzeń wektorową V można traktować jako przestrzeń afiniczną nad samą sobą. Oznacza to, że każdy element V może być traktowany albo jako punkt, albo jako wektor. Ta przestrzeń afiniczna jest czasami oznaczana ( V , V ) dla podkreślenia podwójnej roli elementów V . Rozważany jako punkt, wektor zerowy jest zwykle oznaczany jako o (lub O , gdy dla punktów używane są duże litery) i nazywany początkiem .

Jeśli A jest inną przestrzenią afiniczną w tej samej przestrzeni wektorowej (to $),$ wybór dowolnego punktu a w A definiuje unikalny izomorfizm afiniczny, z V i odwzorowuje a na o . Innymi słowy, wybór pochodzenia a w A pozwala nam zidentyfikować A i ( V , V ) aż do kanonicznego izomorfizmu . Odpowiednikiem tej własności jest to, że przestrzeń afiniczną A można utożsamiać z przestrzenią wektorową V , w której „zapomniano miejsce pochodzenia”.

Stosunek do przestrzeni euklidesowych

Definicja przestrzeni euklidesowych

Przestrzenie euklidesowe (w tym linia jednowymiarowa, płaszczyzna dwuwymiarowa i przestrzeń trójwymiarowa powszechnie badana w geometrii elementarnej, a także analogi o wyższych wymiarach) są przestrzeniami afinicznymi.

Rzeczywiście, w większości współczesnych definicji przestrzeń euklidesowa jest definiowana jako przestrzeń afiniczna, tak że powiązana przestrzeń wektorowa jest rzeczywistą przestrzenią iloczynu wewnętrznego o skończonym wymiarze, to jest przestrzenią wektorową nad liczbami rzeczywistymi z dodatnio określoną formą kwadratową q ( x ) . Iloczyn wewnętrzny dwóch wektorów x i y jest wartością symetrycznej postaci dwuliniowej

${\ Displaystyle x \ cdot y = {\ Frac {1} {2}} (q (x + y) -q (x) -q (y)).}$

Zwykła odległość euklidesowa między dwoma punktami A i B wynosi

${\ Displaystyle d (A, B) = {\ sqrt {q (BA)}}.}$

W starszej definicji przestrzeni euklidesowych za pomocą geometrii syntetycznej wektory są definiowane jako klasy równoważności uporządkowanych par punktów w warunkach równoważności (pary ( A , B ) i ( C , D ) są równoważne, jeśli punkty A , B , D , C ( w tej kolejności) tworzą równoległobok ). Łatwo jest sprawdzić, czy wektory tworzą przestrzeń wektorową, kwadrat odległości euklidesowej jest formą kwadratową na przestrzeni wektorów, a dwie definicje przestrzeni euklidesowych są równoważne.

Właściwości afiniczne

W geometrii euklidesowej powszechne wyrażenie „ właściwość afiniczna ” odnosi się do właściwości, której można dowieść w przestrzeniach afinicznych, to znaczy można ją udowodnić bez użycia formy kwadratowej i związanego z nią iloczynu wewnętrznego. Innymi słowy, właściwość afiniczna to właściwość, która nie obejmuje długości i kątów. Typowymi przykładami są równoległość i definicja stycznej . Nie-przykładem jest definicja normalnego .

Równoważnie, właściwość afiniczna jest właściwością, która jest niezmienna w przypadku przekształceń afinicznych przestrzeni euklidesowej.

Kombinacje afiniczne i środek ciężkości

Niech a ₁ , ..., a _n będzie zbiorem n punktów w przestrzeni afinicznej i będzie ${\ Displaystyle \ lambda _ {1}, \ kropki, \ lambda _ {n}}$ n elementów pola naziemnego .

Załóżmy, że ${\ Displaystyle \ lambda _ {1} + \ kropki + \ lambda _ {n} = 0}$ . Dla dowolnych dwóch punktów o i o' jeden ma

${\ Displaystyle \ lambda _ {1} {\ overrightarrow {oa_ {1}}} + \ kropki + \ lambda _ {n} {\ overrightarrow {oa_ {n}}} = \ lambda _ {1} {\ overrightarrow { o'a_{1}}}+\kropki +\lambda _{n}{\overrightarrow {o'a_{n}}}.}$

Zatem suma ta jest niezależna od wyboru pochodzenia, a wynikowy wektor można oznaczyć

${\ Displaystyle \ lambda _ {1} a_ {1} + \ kropki + \ lambda _ {n} a_ {n}.}$

Kiedy ${\ Displaystyle n = 2, \ lambda _ {1} = 1, \ lambda _ {2} = -1}$ , uzyskuje się definicję odejmowania zwrotnica.

Załóżmy teraz, że elementy pola spełniają ${\ Displaystyle \ lambda _ {1} + \ kropki + \ lambda _ {n} = 1}$ . Dla pewnego wyboru pochodzenia o , oznacz przez unikalny punkt taki, że ${\ displaystyle g}$

${\ Displaystyle \ lambda _ {1} {\ overrightarrow {oa_ {1}}} + \ kropki + \ lambda _ {n} {\ overrightarrow {oa_ {n}}} = {\ overrightarrow {og}}.}$

Można pokazać, że $niezależny$ od wyboru o . Dlatego jeśli

${\ Displaystyle \ lambda _ {1} + \ kropki + \ lambda _ {n} = 1,}$

można napisać

${\ Displaystyle g = \ lambda _ {1} a_ {1} + \ kropki + \ lambda _ {n} a_ {n}.}$

Punkt $displaystyle$ jest środkiem barycentrum ciężarów . $a_ {i$ { $}$ . Mówi się również, że $}$$}$ współczynników za ja { $a_ {i$ .

Przykłady

• Kiedy dzieci znajdują odpowiedzi na sumy takie jak 4 + 3 lub 4 − 2, licząc w prawo lub w lewo na osi liczbowej , traktują oś liczbową jako jednowymiarową przestrzeń afiniczną.
• Przestrzeń energii jest przestrzenią afiniczną dla $.$ ponieważ często nie ma sensu mówić o energii absolutnej, ale sensowne jest mówienie o różnicach energii Energia próżni , gdy jest zdefiniowana, ma pochodzenie kanoniczne.
• Przestrzeń fizyczna $jest$ często modelowana jako przestrzeń afiniczna dla w ustawieniach nierelatywistycznych i ${\ Displaystyle \ mathbb {R} ^ {1,3$ w warunkach relatywistycznych. Aby odróżnić je od przestrzeni wektorowej, są one czasami nazywane przestrzeniami euklidesowymi ${\ Displaystyle {\ tekst {E}} (3)}$ i ${\ Displaystyle {\ tekst {E}} (1 ,3)}$ .
• Każdy kozbiór podprzestrzeni V przestrzeni wektorowej jest przestrzenią afiniczną nad tą podprzestrzenią.
• Jeśli T jest macierzą , Tx =0 a b leży w jej przestrzeni kolumnowej , to zbiór rozwiązań równania Tx = b jest przestrzenią afiniczną nad podprzestrzenią rozwiązań .
• Rozwiązania niejednorodnego liniowego równania różniczkowego tworzą przestrzeń afiniczną nad rozwiązaniami odpowiedniego jednorodnego równania liniowego.
• Uogólniając wszystkie powyższe, jeśli T : V → W jest mapą liniową i y leży w jej obrazie, zbiór rozwiązań x ∈ V równania T x = y jest kozbiorem jądra T , a zatem jest przestrzeń afiniczna nad Ker T   .
• Przestrzeń (liniowych) komplementarnych podprzestrzeni podprzestrzeni wektorowej V w przestrzeni wektorowej W jest przestrzenią afiniczną nad Hom( W / V , V ) . To znaczy, jeśli 0 → V → W → X → 0 jest krótkim dokładnym ciągiem przestrzeni wektorowych, to przestrzeń wszystkich rozszczepień ciągu dokładnego w naturalny sposób przenosi strukturę przestrzeni afinicznej nad Hom( X , V ) .
• Przestrzeń połączeń (patrząc z $jest$ wektorów , gdzie jest gładką rozmaitością $)$ przestrzenią ${\ Displaystyle {\ tekst {koniec}} (E)}$ o wartości 1-formy. Przestrzeń połączeń (patrząc z głównej wiązki $)$ przestrzenią afiniczną dla przestrzeni wektorowej $ad}} (P)}$ -formy o wartości 1, gdzie ${\ Displaystyle {\ text {ad}} (P)}$ jest powiązaną wiązką przylegającą.

Rozpiętość afiniczna i podstawy

Dla każdego podzbioru X przestrzeni afinicznej A istnieje najmniejsza podprzestrzeń afiniczna, która go zawiera, zwana rozpiętością afiniczną X . Jest to przecięcie wszystkich podprzestrzeni afinicznych zawierających X , a jej kierunek jest przecięciem kierunków podprzestrzeni afinicznych zawierających X .

Afiniczna rozpiętość X to zbiór wszystkich ( skończonych) afinicznych kombinacji punktów X , a jej kierunek to liniowa rozpiętość x w - y dla x i y X . Jeśli wybierzemy określony punkt x ₀ , kierunek rozpiętości afinicznej X jest jednocześnie rozpiętością liniową x – x ₀ dla x w X .

Mówi się również, że rozpiętość afiniczna X jest generowana przez X i że X jest zbiorem generującym jej rozpiętość afiniczną.

zbiór X punktów przestrzeni afinicznej jest afinicznie niezależny lub po prostu niezależny , jeśli rozpiętość afiniczna dowolnego ścisłego podzbioru X jest ścisłym podzbiorem rozpiętości afinicznej X . Podstawa afiniczna lub rama barycentryczna (patrz § Współrzędne barycentryczne poniżej) przestrzeni afinicznej jest również niezależnym zespołem generującym (czyli minimalnym zespołem generującym).

Przypomnijmy, że wymiar przestrzeni afinicznej jest wymiarem związanej z nią przestrzeni wektorowej. Podstawami przestrzeni afinicznej o skończonym wymiarze n są niezależne podzbiory n + 1 elementów lub równoważnie generujące podzbiory n + 1 elementów. Równoważnie ₀ { x , ..., x _n } jest bazą afiniczną przestrzeni afinicznej wtedy i tylko wtedy, gdy ₀ { x ₁ - x , ..., x _n - x ₀ } jest bazą liniową powiązanej przestrzeni wektorowej.

Istnieją dwa silnie powiązane rodzaje układów współrzędnych , które można zdefiniować w przestrzeniach afinicznych.

Współrzędne barycentryczne

Zobacz też: Barycentryczny układ współrzędnych

Niech A $_$ przestrzenią o n nad polem k i _ _ Właściwości podstawy afinicznej implikują, że dla każdego x w A istnieje unikalny ( n + 1) - krotka ${\ Displaystyle (\ lambda _ {0}, \ kropki, \ lambda _ { n})}$ elementów k takich, że

${\ Displaystyle \ lambda _ {0} + \ kropki + \ lambda _ {n} = 1}$

I

${\ Displaystyle x = \ lambda _ {0}x_ {0} + \ kropki + \ lambda _ {n} x_ {n}.}$

λ ${\ Displaystyle \ lambda _ {i}}$ nazywane są współrzędnymi barycentrycznymi x na podstawie afinicznej $\ Displaystyle \ {x_ {0}, \ kropki, x_ {n}$ x . Jeśli x _{i są postrzegane jako ciała,} które _ja mają ciężary (lub masy) ${\ displaystyle \ lambda _ {i}}$ punkt x jest zatem środkiem barycentrum x , co wyjaśnia pochodzenie terminu współrzędne barycentryczne λ .

Współrzędne barycentryczne definiują izomorfizm afiniczny między przestrzenią afiniczną A a podprzestrzenią afiniczną k ^{n + 1} określoną równaniem ${\ Displaystyle \ lambda _ {0} + \ kropki + \ lambda _ { n}=1}$ .

W przypadku przestrzeni afinicznych o nieskończonym wymiarze obowiązuje ta sama definicja, używając tylko skończonych sum. Oznacza to, że dla każdego punktu tylko skończona liczba współrzędnych jest różna od zera.

Współrzędne afiniczne

Układ afiniczny przestrzeni afinicznej składa się z punktu zwanego początkiem i liniowej podstawy powiązanej przestrzeni wektorowej. Dokładniej, dla przestrzeni afinicznej ( A ₁ , ..., v _, ) z $A$ przestrzenią wektorową początek o należy do , a podstawa liniowa jest podstawą n z ${\ displaystyle {\ overrightarrow {A}}}$ (dla uproszczenia notacji rozważamy tylko przypadek skończonego wymiaru, ogólny przypadek jest podobny).

$Dla$ każdego p A istnieje sekwencja ,

${\ Displaystyle p = o + \ lambda _ {1} v_ {1} + \ kropki + \ lambda _ {n} v_ {n},}$

lub równoważnie

${\ Displaystyle {\ overrightarrow {op}} = \ lambda _ {1} v_ {1} + \ kropki + \ lambda _ {n} v_ {n}.}$

λ $\ lambda _ {i}}$ displaystyle o , v ₁ , ..., v _n ) nazywane są współrzędnymi afinicznymi p nad ramką afiniczną .

Przykład: W geometrii euklidesowej współrzędne kartezjańskie są współrzędnymi afinicznymi względem układu ortonormalnego , czyli układu afinicznego ( o , v ₁ , ..., v _n ) takiego, że ( v ₁ , ..., v _n ) jest baza ortonormalna .

Związek między współrzędnymi barycentrycznymi i afinicznymi

Współrzędne barycentryczne i współrzędne afiniczne są ze sobą silnie powiązane i można je uznać za równoważne.

W rzeczywistości, biorąc pod uwagę układ barycentryczny

${\ Displaystyle (x_ {0}, \ kropki, x_ {n}),}$

od razu dedukuje się ramę afiniczną

${\ Displaystyle (x_ {0}, {\ overrightarrow {x_ {0} x_ {1}}},\kropki,{\overrightarrow {x_{0}x_{n}}})=\lewo(x_{0},x_{1}-x_{0},\kropki,x_{n} -x_{0}\po prawej),}$

i jeśli

${\ Displaystyle \ lewo (\ lambda _ {0}, \ lambda _ {1}, \ kropki, \ lambda _ {n} \ prawej)}$

są współrzędnymi barycentrycznymi punktu na układzie barycentrycznym, to współrzędne afiniczne tego samego punktu na układzie afinicznym to

${\ Displaystyle \ lewo (\ lambda _ {1}, \ kropki, \ lambda _ {n} \ prawo).}$

I odwrotnie, jeśli

${\ Displaystyle \ lewo (o, v_ {1}, \ kropki, v_ {n} \ prawej)}$

jest zatem układem afinicznym

${\ Displaystyle \ lewo (o, o + v_ {1}, \ kropki, o + v_ {n} \ prawo)}$

jest układem barycentrycznym. Jeśli

${\ Displaystyle \ lewo (\ lambda _ {1}, \ kropki, \ lambda _ {n} \ prawej)}$

są współrzędnymi afinicznymi punktu na układzie afinicznym, to jego współrzędne barycentryczne na układzie barycentrycznym to

${\ Displaystyle \ lewo (1- \ lambda _ {1} - \ kropki - \ lambda _ {n}, \ lambda _ {1}, \ kropki, \ lambda _ {n} \ prawej).}$

Dlatego współrzędne barycentryczne i afiniczne są prawie równoważne. W większości zastosowań preferowane są współrzędne afiniczne, ponieważ obejmują mniej współrzędnych, które są niezależne. Jednak w sytuacjach, gdy ważne punkty badanego problemu są afinicznie niezależne, współrzędne barycentryczne mogą prowadzić do prostszych obliczeń, jak w poniższym przykładzie.

Przykład trójkąta

Wierzchołki niepłaskiego trójkąta tworzą afiniczną podstawę płaszczyzny euklidesowej . Współrzędne barycentryczne umożliwiają łatwą charakterystykę elementów trójkąta, które nie obejmują kątów ani odległości:

Wierzchołki to punkty o współrzędnych barycentrycznych (1, 0, 0) , (0, 1, 0) i (0, 0, 1) . Linie podtrzymujące krawędzie to punkty, które mają zerową współrzędną. Same krawędzie to punkty, które mają jedną współrzędną zerową i dwie współrzędne nieujemne. Wnętrze trójkąta to punkty, których wszystkie współrzędne są dodatnie. Mediany to , 1/3 , współrzędnych 1/3 a środek 1/3 ciężkości to , ) punkty, które mają dwie równe współrzędne punkt o ( .

Własności homomorfizmów afinicznych

Obraz i włókna

Pozwalać

${\ displaystyle f \ dwukropek E \ do fa}$

być homomorfizmem afinicznym, z

${\ Displaystyle {\ overrightarrow {f}} \ okrężnica {\ overrightarrow {E}} \ do {\ overrightarrow {F}}}$

jako powiązana mapa liniowa.

Obraz f jest podprzestrzenią afiniczną f ( E ) z fa , która ma powiązaną przestrzeń wektorową ${\ displaystyle {\ overrightarrow {f}} ({\ overrightarrow {E}})} .$ Ponieważ przestrzeń afiniczna nie ma elementu zerowego , homomorfizm afiniczny nie ma jądra . Jednak dla dowolnego punktu x z f ( mi ) , obraz odwrotny f ^–1 ( x ) jest podprzestrzenią afiniczną mi , o kierunku ${\ Displaystyle {\ overrightarrow {f}} ^ {- 1}(x)}$ . Ta podprzestrzeń afiniczna nazywana jest włóknem x .

Występ

Zobacz też: Projekcja (matematyka)

Ważnym przykładem jest rzut równoległy do ​​pewnego kierunku na podprzestrzeń afiniczną. Znaczenie tego przykładu polega na tym, że przestrzenie euklidesowe są przestrzeniami afinicznymi i że tego rodzaju projekcje są fundamentalne w geometrii euklidesowej .

Dokładniej, biorąc pod uwagę przestrzeń afiniczną E z powiązaną przestrzenią wektorową , niech F będzie podprzestrzenią afiniczną o kierunku $}}$$displaystyle {\ overrightarrow {$ i D być komplementarną podprzestrzenią w ${\ displaystyle {\ overrightarrow {E}}}$$($ oznacza to, że każdy wektor $}} można rozłożyć$$\ overrightarrow {E}$ } $.$ unikalny sposób jako sumę elementu elementu D ) Dla każdego punktu x z E , jego rzut na F równoległy do ​​D jest unikalnym punktem p ( x ) w F takim, że

${\ Displaystyle p (x) -x \ w D.}$

Jest to homomorfizm afiniczny, którego powiązana mapa liniowa jest zdefiniowana przez ${\ displaystyle {\ overrightarrow {p}}}$

${\ Displaystyle {\ overrightarrow {p}} (xy) = p (x) -p (y)}$

dla x i y w E .

Obrazem tej projekcji jest F , a jej włóknami są podprzestrzenie o kierunku D .

Przestrzeń ilorazowa

Chociaż jądra nie są zdefiniowane dla przestrzeni afinicznych, zdefiniowane są przestrzenie ilorazowe. Wynika to z faktu, że „przynależność do tego samego włókna homomorfizmu afinicznego” jest relacją równoważności.

Niech E będzie przestrzenią afiniczną, a D będzie liniową podprzestrzenią powiązanej przestrzeni wektorowej ${\ displaystyle {\ overrightarrow {E}}}$ . Iloraz E / D E przez D jest ilorazem E przez relację równoważności taką, że x i y są równoważne , jeśli

${\ displaystyle xy \ w D.}$

$jest$ przestrzenią afiniczną, która ma wektorową

Dla każdego homomorfizmu afinicznego $izomorficzny$ ilorazem E przez powiązanej mapy liniowej. Jest to pierwsze twierdzenie o izomorfizmie dla przestrzeni afinicznych.

Aksjomaty

Przestrzenie afiniczne są zwykle badane za pomocą geometrii analitycznej przy użyciu współrzędnych lub równoważnych przestrzeni wektorowych. Można je również badać jako geometrię syntetyczną , zapisując aksjomaty, chociaż takie podejście jest znacznie mniej powszechne. Istnieje kilka różnych systemów aksjomatów dla przestrzeni afinicznej.

Coxeter (1969 , s. 192) aksjomatyzuje szczególny przypadek geometrii afinicznej nad liczbami rzeczywistymi jako geometrię uporządkowaną wraz z afiniczną postacią twierdzenia Desarguesa i aksjomatem stwierdzającym, że na płaszczyźnie istnieje co najwyżej jedna prosta przechodząca przez dany punkt, która nie spełnia dana linia.

Płaszczyzny afiniczne spełniają następujące aksjomaty ( Cameron 1991 , rozdział 2): (w którym dwie proste nazywane są równoległymi, jeśli są równe lub rozłączne):

• Dowolne dwa różne punkty leżą na jednej prostej.
• Biorąc pod uwagę punkt i linię, istnieje unikalna linia, która zawiera punkt i jest równoległa do linii
• Istnieją trzy niewspółliniowe punkty.

Oprócz płaszczyzn afinicznych nad ciałami (lub pierścieniami podziału ), istnieje również wiele płaszczyzn niedesargueskich spełniających te aksjomaty. ( Cameron 1991 , rozdział 3) podaje aksjomaty dla wielowymiarowych przestrzeni afinicznych.

Czysto aksjomatyczna geometria afiniczna jest bardziej ogólna niż przestrzenie afiniczne i jest omówiona w osobnym artykule .

Stosunek do przestrzeni rzutowych

Przestrzeń afiniczna to podprzestrzeń przestrzeni rzutowej, która z kolei jest ilorazem przestrzeni wektorowej przez relację równoważności (nie przez podprzestrzeń liniową)

Przestrzenie afiniczne są zawarte w przestrzeniach rzutowych . Na przykład płaszczyznę afiniczną można uzyskać z dowolnej płaszczyzny rzutowej , usuwając jedną linię i wszystkie znajdujące się na niej punkty, i odwrotnie, dowolnej płaszczyzny afinicznej można użyć do skonstruowania płaszczyzny rzutowej jako domknięcia przez dodanie linii w nieskończoności , której punkty odpowiadają klasy równoważności prostych równoległych . Podobne konstrukcje utrzymują się w wyższych wymiarach.

Co więcej, transformacje przestrzeni rzutowej, które zachowują przestrzeń afiniczną (równoważnie, które pozostawiają hiperpłaszczyznę w nieskończoności niezmienną jako zbiór ) dają transformacje przestrzeni afinicznej. I odwrotnie, każda afiniczna transformacja liniowa rozciąga się wyłącznie na rzutową transformację liniową, więc grupa afiniczna jest podgrupą grupy rzutowej . Na przykład transformacje Möbiusa (transformacje zespolonej linii rzutowej lub sfery Riemanna ) są afiniczne (transformacje płaszczyzny zespolonej) wtedy i tylko wtedy, gdy ustalają punkt w nieskończoności .

Afiniczna geometria algebraiczna

W geometrii algebraicznej rozmaitość afiniczna (lub bardziej ogólnie afiniczny zbiór algebraiczny ) definiuje się jako podzbiór przestrzeni afinicznej, który jest zbiorem wspólnych zer zbioru tak zwanych funkcji wielomianowych w przestrzeni afinicznej . Aby zdefiniować funkcję wielomianową w przestrzeni afinicznej , należy wybrać układ afiniczny . Wtedy funkcja wielomianu jest funkcją taką, że obraz dowolnego punktu jest wartością jakiejś wielowymiarowej funkcji wielomianu współrzędnych punktu. Ponieważ zmianę współrzędnych afinicznych można wyrazić funkcjami liniowymi (dokładniej funkcjami afinicznymi) współrzędnych, definicja ta jest niezależna od konkretnego wyboru współrzędnych.

Wybór układu współrzędnych afinicznych dla przestrzeni afinicznej $}$ { \ Displaystyle \ mathbb { A } $n}}$ i afiniczna przestrzeń współrzędnych k ⁿ . To wyjaśnia $wprowadza$ dlaczego dla uproszczenia wiele podręczników pisze zera funkcje wielomianowe nad k ⁿ .

Ponieważ cała przestrzeń afiniczna jest zbiorem wspólnych zer wielomianu zerowego , przestrzenie afiniczne są algebraicznymi odmianami afinicznymi.

Pierścień funkcji wielomianowych

Zgodnie z powyższą definicją wybór układu afinicznego przestrzeni afinicznej pozwala na zidentyfikowanie funkcji wielomianu na $^ {n}}$$displaystyle \ mathbb {$ z wielomianami w n zmiennych, gdzie i- ta zmienna reprezentuje funkcję, która odwzorowuje punkt na jego i- tą współrzędną. Wynika z $ZA$${\ Displaystyle k \ lewo$ że zbiór funkcji wielomianowych nad to \ -algebra , oznaczona , który jest izomorficzny z pierścieniem wielomianowym ${\ Displaystyle k \ lewo [X_ {1}, \ kropki, X_ {n}\prawo]}$ .

Kiedy zmienia się współrzędne, izomorfizm między ${\ Displaystyle k \ lewo [\ mathbb {A} _ {k} ^ {n} \ prawej]}$ i ${ \ displaystyle k [X_ {1}, \ kropki, X_ {n}]}$ odpowiednio się zmienia, a to wywołuje automorfizm ${\ Displaystyle k \ lewo [X_ {1}, \ dots ,X_{n}\right]}$ , które odwzorowuje każdy nieokreślony na wielomian stopnia pierwszego. Wynika z tego, że $całkowity$ stopień definiuje filtrację która . Stopień całkowity określa również podziałkę , ale zależy to od doboru współrzędnych, gdyż zmiana współrzędnych afinicznych może odwzorowywać nieoznaczoności na wielomianach niejednorodnych .

Topologia Zariskiego

Zobacz też: topologia Zariskiego

Przestrzenie afiniczne nad ciałami topologicznymi , takie jak liczby rzeczywiste lub zespolone, mają topologię naturalną . Topologia Zariskiego, która jest zdefiniowana dla przestrzeni afinicznych nad dowolnym polem, pozwala w każdym przypadku na użycie metod topologicznych. Topologia Zariskiego to unikalna topologia przestrzeni afinicznej, której zbiory domknięte są zbiorami afinicznymi algebraicznymi (czyli zbiorami wspólnych zer funkcji wielomianowych na zbiorze afinicznym). Ponieważ w polu topologicznym funkcje wielomianowe są ciągłe, każdy zbiór domknięty Zariskiego jest domknięty dla zwykłej topologii, jeśli taka istnieje. Innymi słowy, w polu topologicznym topologia Zariskiego jest bardziej zgrubna niż topologia naturalna.

Istnieje naturalna funkcja iniekcyjna z przestrzeni afinicznej do zbioru ideałów pierwszych (czyli widma ) jej pierścienia funkcji wielomianowych. Po wybraniu $odwzorowuje$${\ Displaystyle \ lewo \ langle X_ {1} -a_ {1}, \ kropki, X_ {n} -a_ {n} \ prawo \ rangle}$ na . Funkcja ta jest homeomorfizmem ( dla topologii Zariskiego przestrzeni afinicznej i widma pierścienia funkcji wielomianowych) przestrzeni afinicznej na obraz funkcji.

Przypadek algebraicznie zamkniętego pola podstawowego jest szczególnie ważny w geometrii algebraicznej, ponieważ w tym przypadku powyższy homeomorfizm jest mapą między przestrzenią afiniczną a zbiorem wszystkich maksymalnych ideałów pierścienia funkcji (to jest Nullstellensatz Hilberta ) .

Taka jest idea wyjściowa teorii schematów Grothendiecka , która polega na uznawaniu za „ punkty” nie tylko punktów przestrzeni afinicznej, ale także wszystkich ideałów pierwszych widma w celu badania rozmaitości algebraicznych. Pozwala to na sklejanie rozmaitości algebraicznych w podobny sposób, jak w przypadku rozmaitości skleja się wykresy w celu zbudowania rozmaitości.

Kohomologia

Podobnie jak wszystkie odmiany afiniczne, lokalne dane w przestrzeni afinicznej zawsze można połączyć globalnie: kohomologia przestrzeni afinicznej jest trywialna. ${\ Displaystyle H ^ {i} \ lewo (\ mathbb {A} _ {k} ^ {n}, \ mathbf {F} \ prawej) = 0$ ja dla wszystkie spójne snopy fa i liczby całkowite ${\ displaystyle i> 0}$ . Z tej właściwości korzystają również wszystkie inne odmiany pokrewne . Ale także wszystkie kohomologii etale w przestrzeni afinicznej są trywialne. W szczególności każda wiązka linii jest trywialna. Mówiąc bardziej ogólnie, twierdzenie Quillena-Suslina implikuje, że każda wiązka wektorów algebraicznych w przestrzeni afinicznej jest trywialna.

Zobacz też

• Kadłub afiniczny - najmniejsza podprzestrzeń afiniczna zawierająca podzbiór
• Złożona przestrzeń afiniczna - Przestrzeń afiniczna nad liczbami zespolonymi
• Egzotyczna przestrzeń afiniczna - Rzeczywista przestrzeń afiniczna o parzystym wymiarze, która nie jest izomorficzna ze złożoną przestrzenią afiniczną
• Przestrzeń (matematyka) - zestaw matematyczny z pewną dodaną strukturą
• Barycentryczny układ współrzędnych

Notatki

•   Berger, Marcel (1984), „Przestrzenie afiniczne” , Problemy geometrii , Springer-Verlag, ISBN 978-0-387-90971-4
•   Berger, Marcel (1987), Geometria I , Berlin: Springer, ISBN 3-540-11658-3
•   Cameron, Peter J. (1991), Przestrzenie rzutowe i biegunowe , QMW Maths Notes, tom. 13, Londyn: Queen Mary and Westfield College School of Mathematical Sciences, MR 1153019
•    Coxeter, Harold Scott MacDonald (1969), Wprowadzenie do geometrii (wyd. 2), Nowy Jork: John Wiley & Sons , ISBN 978-0-471-50458-0 , MR 0123930
• Dołgaczow, IV ; Shirokov, AP (2001) [1994], „Przestrzeń afiniczna” , Encyklopedia matematyki , EMS Press
•    Hartshorne, Robin (1977). Geometria algebraiczna . Springer-Verlag . ISBN 978-0-387-90244-9 . Zbl 0367.14001 .
•   Nomizu, K .; Sasaki, S. (1994), afiniczna geometria różniczkowa (nowe wyd.), Cambridge University Press, ISBN 978-0-521-44177-3
•   Snapper, Ernst ; Troyer, Robert J. (1989), Metric Affine Geometry (wydanie Dover, po raz pierwszy opublikowane w 1989 r.), Dover Publications, ISBN 0-486-66108-3
•   Reventós Tarrida, Agustí (2011), „Przestrzenie afiniczne”, mapy afiniczne, ruchy euklidesowe i kwadratury , Springer, ISBN 978-0-85729-709-9