Wykresy na SO(3)

Szersze omówienie tego tematu można znaleźć w artykule Rotation group SO(3) .

W matematyce , specjalna ortogonalna grupa w trzech wymiarach, inaczej znana jako grupa rotacyjna SO(3) , jest naturalnie występującym przykładem rozmaitości . Różne wykresy w SO(3) tworzą konkurencyjne układy współrzędnych : w tym przypadku nie można powiedzieć, że istnieje preferowany zestaw parametrów opisujących obrót. Istnieją trzy stopnie swobody , więc wymiar SO(3) wynosi trzy. W wielu zastosowaniach używany jest jeden lub drugi układ współrzędnych i powstaje pytanie, jak przekonwertować dany układ na inny.

Przestrzeń obrotów

W geometrii grupa rotacji to grupa wszystkich rotacji wokół początku trójwymiarowej przestrzeni euklidesowej R 3 pod działaniem złożenia . Z definicji obrót wokół początku układu współrzędnych jest przekształceniem liniowym , które zachowuje długość wektorów (jest to izometria ) oraz zachowuje orientację (tj. kierunkowość ) przestrzeni. Transformacja zachowująca długość, która odwraca orientację, nazywana jest obrotem niewłaściwym . Każdy niewłaściwy obrót trójwymiarowej przestrzeni euklidesowej jest obrotem, po którym następuje odbicie w płaszczyźnie przechodzącej przez początek.

Skomponowanie dwóch obrotów skutkuje kolejnym obrotem; każdy obrót ma unikalny obrót odwrotny; a mapa tożsamości spełnia definicję obrotu. Dzięki powyższym właściwościom zbiór wszystkich obrotów jest grupą o złożeniu. Ponadto grupa rotacyjna ma naturalną rozmaitość , dla której operacje grupowe są płynne ; więc w rzeczywistości jest to grupa Kłamców . Grupa rotacyjna jest często oznaczana jako SO(3) z powodów wyjaśnionych poniżej .

Przestrzeń rotacji jest izomorficzna ze zbiorem operatorów obrotu i zbiorem macierzy ortonormalnych z wyznacznikiem +1. Jest również ściśle powiązany ( podwójnie pokryty ) ze zbiorem kwaternionów z ich iloczynem wewnętrznym, a także ze zbiorem wektorów rotacji (choć tutaj zależność jest trudniejsza do opisania, szczegóły poniżej), z inną operacją składu wewnętrznego dany przez iloczyn ich równoważnych macierzy.

Notacja wektorów rotacji wynika z twierdzenia Eulera o rotacji , które mówi, że dowolny obrót w trzech wymiarach można opisać obrotem o pewien kąt wokół pewnej osi. Biorąc to pod uwagę, możemy następnie określić oś jednego z tych obrotów za pomocą dwóch kątów, a promień wektora możemy określić kąt obrotu . Te wektory reprezentują piłkę w 3D o niezwykłej topologii.

Ta bryła sferyczna 3D odpowiada powierzchni dysku 4D, który jest również odmianą 3D. Aby wykonać tę równoważność, będziemy musieli zdefiniować, w jaki sposób będziemy reprezentować obrót za pomocą tej powierzchni osadzonej w 4D.

Hipersfera obrotów

Dwa obroty o różne kąty i różne osie w przestrzeni obrotów. Długość wektora jest związana z wielkością obrotu.

Wizualizacja hipersfery

Interesujące jest rozważenie przestrzeni jako trójwymiarowej kuli S 3 , granicy dysku w 4-wymiarowej przestrzeni euklidesowej. Aby to zrobić, będziemy musieli zdefiniować, w jaki sposób reprezentujemy obrót za pomocą tej powierzchni osadzonej w 4D.

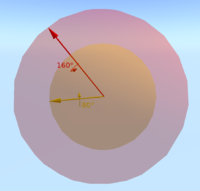
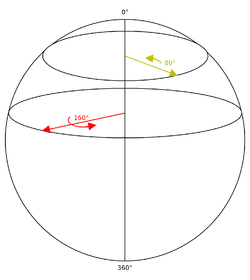
Sposób, w jaki promień może być użyty do określenia kąta obrotu, nie jest prosty. Można to powiązać z okręgami szerokości geograficznej w kuli z określonym biegunem północnym i wyjaśniono w następujący sposób:

Rozpoczynając od bieguna północnego kuli w przestrzeni trójwymiarowej, określamy punkt na biegunie północnym, aby reprezentować obrót tożsamości. W przypadku obrotu tożsamości nie jest zdefiniowana oś obrotu, a kąt obrotu (zero) nie ma znaczenia. Obrót, którego oś zawiera się w xy i bardzo mały kąt obrotu, można określić przecinając kulę równolegle do płaszczyzny xy i bardzo blisko bieguna północnego. Okrąg zdefiniowany przez ten wycinek będzie bardzo mały, odpowiadający małemu kątowi obrotu. Gdy kąty obrotu stają się większe, wycinek przesuwa się na południe, a okręgi stają się większe, aż do osiągnięcia równika kuli, co odpowiada kątowi obrotu 180 stopni. Idąc dalej na południe, promienie okręgów stają się teraz mniejsze (odpowiadające bezwzględnej wartości kąta obrotu traktowanego jako liczba ujemna). Wreszcie, po osiągnięciu bieguna południowego, okręgi ponownie kurczą się do obrotu tożsamości, który jest również określany jako punkt na biegunie południowym. Odnotuj, że za pomocą tej wizualizacji można zobaczyć cały szereg cech takich obrotów i ich reprezentacji.

Przestrzeń obrotów jest ciągła, każdy obrót ma sąsiedztwo obrotów, które są prawie takie same, a sąsiedztwo to staje się płaskie w miarę kurczenia się sąsiedztwa.

Skróty

Hipersfera obrotów dla obrotów, które mają oś „poziomą” (w płaszczyźnie xy ).

Ponadto każdy obrót jest w rzeczywistości reprezentowany przez dwa antypodalne punkty na kuli, które znajdują się na przeciwległych końcach linii przechodzącej przez środek kuli. Odzwierciedla to fakt, że każdy obrót można przedstawić jako obrót wokół jakiejś osi lub równoważnie jako ujemny obrót wokół osi skierowanej w przeciwnym kierunku (tzw. podwójna osłona ) . „Szerokość geograficzna” okręgu reprezentującego określony kąt obrotu będzie równa połowie kąta reprezentowanego przez ten obrót, ponieważ gdy punkt jest przesuwany z bieguna północnego na południowy, szerokość geograficzna waha się od zera do 180 stopni, podczas gdy kąt obrotu mieści się w zakresie od 0 do 360 stopni . („długość geograficzna” punktu reprezentuje wówczas określoną oś obrotu). Należy jednak zauważyć, że ten zestaw obrotów nie jest zamknięty w kompozycji.

Dwa kolejne obroty z osiami w płaszczyźnie xy niekoniecznie dadzą obrót, którego oś leży w płaszczyźnie xy , a zatem nie może być przedstawiony jako punkt na kuli. Nie będzie tak w przypadku ogólnego obrotu w przestrzeni 3, które tworzą zbiór zamknięty w ramach kompozycji.

Wizualizację tę można rozszerzyć do ogólnego obrotu w przestrzeni trójwymiarowej. Obrót tożsamości jest punktem, a mały kąt obrotu wokół pewnej osi można przedstawić jako punkt na kuli o małym promieniu. Gdy kąt obrotu rośnie, kula rośnie, aż kąt obrotu osiągnie 180 stopni, w którym to momencie kula zaczyna się kurczyć, stając się punktem, gdy kąt zbliża się do 360 stopni (lub zero stopni od kierunku ujemnego). Ten zestaw rozszerzających się i kurczących sfer reprezentuje hipersferę w przestrzeni czterowymiarowej (3-sferę).

Podobnie jak w prostszym przykładzie powyżej, każdemu obrotowi reprezentowanemu jako punkt na hipersferze odpowiada jego antypodalny punkt na tej hipersferze. „Szerokość geograficzna” hipersfery będzie równa połowie odpowiedniego kąta obrotu, a sąsiedztwo dowolnego punktu stanie się „bardziej płaskie” (tj. będzie reprezentowane przez trójwymiarową euklidesową przestrzeń punktów) w miarę zmniejszania się sąsiedztwa.

To zachowanie jest dopasowane przez zestaw kwaternionów jednostkowych : Ogólny kwaternion reprezentuje punkt w przestrzeni czterowymiarowej, ale ograniczenie go do wielkości jednostkowej daje trójwymiarową przestrzeń równoważną powierzchni hipersfery. Wielkość kwaternionu jednostkowego będzie jednością, odpowiadającą hipersferze o jednostkowym promieniu.

Część wektorowa kwaternionu jednostkowego reprezentuje promień 2-kuli odpowiadający osi obrotu, a jej wielkość jest sinusem połowy kąta obrotu. Każdy obrót jest reprezentowany przez dwa kwaterniony jednostkowe o przeciwnych znakach i podobnie jak w przestrzeni rotacji w trzech wymiarach iloczyn kwaternionów dwóch kwaternionów jednostkowych da jednostkowy kwaternion. Ponadto przestrzeń kwaternionów jednostkowych jest „płaska” w każdym nieskończenie małym sąsiedztwie danego kwaternionu jednostkowego.

parametryzacje

Główny artykuł: Orientacja (geometria)

Przestrzeń rotacji możemy sparametryzować na kilka sposobów, ale degeneracje zawsze się pojawią. Na przykład, jeśli użyjemy trzech kątów ( kątów Eulera ), taka parametryzacja jest zdegenerowana w niektórych punktach na hipersferze, co prowadzi do problemu blokady gimbala . Możemy tego uniknąć, używając czterech współrzędnych euklidesowych w , x , y , z , gdzie w 2 + x 2 + y 2 + z 2 = 1. Punkt ( w , x , y , z ) reprezentuje obrót wokół osi skierowanej przez wektor ( x , y , z ) przez kąt

Ten problem jest podobny do parametryzacji dwuwymiarowej powierzchni kuli za pomocą dwóch współrzędnych, takich jak szerokość i długość geograficzna. Szerokość i długość geograficzna są źle zachowane ( zdegenerowane ) na biegunach północnym i południowym, chociaż bieguny nie różnią się wewnętrznie od innych punktów na kuli. Na biegunach (szerokości geograficzne +90° i -90°) długość geograficzna staje się bez znaczenia. Można wykazać, że żaden dwuparametrowy układ współrzędnych nie może uniknąć takiej degeneracji.

Potencjalni kandydaci do parametryzacji to:

Problemy parametryzacji

Istnieją problemy z używaniem ich jako czegoś więcej niż wykresów lokalnych, co wiąże się z ich wielowartościowym charakterem i osobliwościami. Oznacza to, że należy przede wszystkim uważać, aby w definicji wykresu pracować tylko z dyfeomorfizmami . Problemy tego rodzaju są nieuniknione, ponieważ SO(3) jest dyfeomorficzne z rzeczywistą przestrzenią rzutową P 3 ( R ), która jest ilorazem S 3 poprzez identyfikację punktów antypodalnych, a wykresy próbują modelować rozmaitość za pomocą R 3 .

To wyjaśnia, dlaczego na przykład kąty Eulera wydają się dawać zmienną w 3- torusie , a kwaterniony jednostkowe w 3-sferze . Wyjątkowość reprezentacji kątami Eulera załamuje się w niektórych punktach (por. Blokada gimbala ), podczas gdy reprezentacja kwaternionów jest zawsze podwójną osłoną , przy czym q i - q dają ten sam obrót.

Jeśli użyjemy macierzy skośno-symetrycznej, każda macierz skośno-symetryczna 3 × 3 jest określona przez 3 parametry, więc na pierwszy rzut oka przestrzeń parametrów to R 3 . Potęgowanie takiej macierzy daje w rezultacie macierz ortogonalną 3 × 3 wyznacznika 1 – innymi słowy macierz rotacji, ale jest to mapa wiele do jednego. Zauważ, że nie jest to mapa pokrywająca – chociaż jest to lokalny homeomorfizm w pobliżu początku, nie jest to mapa pokrywająca przy obrocie o 180 stopni. Możliwe jest ograniczenie tych macierzy do kuli wokół początku układu współrzędnych w R 3 tak, aby obroty nie przekraczały 180 stopni, i to będzie jeden do jednego, z wyjątkiem obrotów o 180 stopni, które odpowiadają granicy S 2 , a te identyfikują punkty antypodalne – to jest miejsce cięcia . Kula 3 z tą identyfikacją granicy to P 3 ( R ). Podobna sytuacja dotyczy zastosowania transformaty Cayleya do macierzy skośno-symetrycznej.

Kąt osi daje parametry w S 2 × S 1 ; jeśli zastąpimy wektor jednostkowy rzeczywistą osią obrotu, tak że n i − n dają tę samą linię osi, zbiór osi staje się P 2 ( R ), rzeczywistą płaszczyzną rzutową . Ale ponieważ obroty wokół n i − n są sparametryzowane przez przeciwne wartości θ, wynikiem jest wiązka S 1 nad P 2 ( R ), która okazuje się być P 3 ( R ).

Ułamkowe przekształcenia liniowe wykorzystują cztery parametry zespolone, a , b , c i d , pod warunkiem, że ad − bc jest niezerowe. Ponieważ pomnożenie wszystkich czterech parametrów przez tę samą liczbę zespoloną nie zmienia parametru, możemy upierać się, że ad − bc = 1. Sugeruje to zapis ( a , b , c , d ) jako macierz zespoloną 2 × 2 wyznacznika 1, czyli jako element specjalnej grupy liniowej SL(2, C ). Ale nie wszystkie takie macierze wytwarzają rotacje: uwzględnione są również mapy konforemne na S 2 . Aby uzyskać tylko obroty, nalegamy, aby d było zespolonym koniugatem a , a c jest przeciwieństwem zespolonego koniugatu b . Wtedy mamy dwie liczby zespolone, aib , podlegające | | _ 2 +| b | 2 = 1. Jeśli napiszemy a + bj , to jest to kwaterniony o długości jednostkowej.

Ostatecznie, ponieważ R3 nie jest P3 ( R ) , będzie problem z każdym z tych podejść . W niektórych przypadkach musimy pamiętać, że pewne wartości parametrów skutkują tym samym obrotem i aby usunąć ten problem, należy ustawić granice, ale wtedy ścieżka przez ten region w R 3 musi nagle przeskoczyć do innego regionu , gdy przekracza granicę. Blokada gimbala jest problemem, gdy pochodna mapy nie jest pełnym rzędem, co występuje w przypadku kątów Eulera i kątów Taita-Bryana, ale nie w przypadku innych opcji. Reprezentacja kwaternionów nie ma żadnego z tych problemów (jest wszędzie odwzorowaniem dwa do jednego), ale ma 4 parametry z warunkiem (długość jednostkowa), co czasami utrudnia dostrzeżenie trzech dostępnych stopni swobody.

Aplikacje

Jednym z obszarów, w których rozważania te w jakiejś formie stają się nieuniknione, jest kinematyka ciała sztywnego . Jako definicję można przyjąć ideę krzywej w grupie euklidesowej E (3) trójwymiarowej przestrzeni euklidesowej , zaczynając od tożsamości (pozycja początkowa). Podgrupa translacji T z E (3) jest podgrupą normalną , z ilorazem SO(3), jeśli spojrzymy na podgrupę E + (3) tylko izometrii prostych ( co jest rozsądne w kinematyce). Część translacyjną można oddzielić od części obrotowej w standardowej kinematyce Newtona, biorąc pod uwagę ruch środka masy i obroty bryły sztywnej wokół środka masy. Dlatego każdy ruch bryły sztywnej prowadzi bezpośrednio do SO(3), gdy uwzględnimy część translacyjną.

Te identyfikacje ilustrują, że SO(3) jest połączony , ale nie po prostu połączony . Jeśli chodzi o to drugie, w kuli ze zidentyfikowanymi antypodalnymi punktami powierzchni rozważ ścieżkę biegnącą od „bieguna północnego” prosto przez środek w dół do bieguna południowego. Jest to zamknięta pętla, ponieważ biegun północny i południowy są identyfikowane. Tej pętli nie można skurczyć do punktu, ponieważ bez względu na to, jak zdeformujesz pętlę, punkt początkowy i końcowy muszą pozostać antypodalne, w przeciwnym razie pętla „rozejrzy się”. Jeśli chodzi o obroty, pętla ta reprezentuje ciągłą sekwencję obrotów wokół z , rozpoczynającą się i kończącą na obrocie tożsamościowym (tj. serię obrotów o kąt φ, gdzie φ biegnie od 0 do 2π).

Co zaskakujące, jeśli przebiegniesz ścieżkę dwukrotnie, tj. od bieguna północnego w dół do bieguna południowego iz powrotem do bieguna północnego, tak że φ biegnie od 0 do 4π, otrzymasz zamkniętą pętlę, którą można skurczyć do jednego punktu: pierwszy ruch ścieżki w sposób ciągły do ​​powierzchni piłki, nadal dwukrotnie łącząc biegun północny z biegunem południowym. Drugą połowę ścieżki można następnie odbić lustrzanie na antypodalną stronę bez żadnej zmiany ścieżki. Teraz mamy zwykłą zamkniętą pętlę na powierzchni kuli, łączącą biegun północny ze sobą wzdłuż wielkiego koła. To koło można bez problemu skurczyć do bieguna północnego. Balijska sztuczka z talerzem i podobne sztuczki demonstrują to praktycznie.

Ten sam argument można przeprowadzić ogólnie i pokazuje, że grupa podstawowa SO(3) jest grupą cykliczną rzędu 2. W zastosowaniach fizyki nietrywialność grupy podstawowej pozwala na istnienie obiektów znanych jako spinory , i jest ważnym narzędziem w rozwoju twierdzenia o statystyce spinowej .

Uniwersalną osłoną SO(3) jest grupa Kłamstwa o nazwie Spin(3) . Grupa Spin(3) jest izomorficzna ze specjalną grupą unitarną SU(2); jest również dyfeomorficzny w stosunku do jednostki 3-sfery S 3 i może być rozumiany jako grupa kwaternionów jednostkowych (tj. o wartości bezwzględnej 1). Powszechnie wykorzystywany w grafice komputerowej związek między kwaternionami i obrotami jest wyjaśniony w kwaternionach i obrotach przestrzennych . Mapa z S 3 na SO(3), która identyfikuje antypodalne punkty S 3 , jest suriekcyjnym homomorfizmem grup Liego, z jądrem {±1}. Topologicznie ta mapa jest mapą pokrywającą dwa do jednego .

Zobacz też

  1. Bibliografia _ 34, przykł. 14.
Pobrano z „ https://en.wikipedia.org/w/index.php?title=Charts_on_SO(3)&oldid=1099134153 ”