Myriagon
| Myriagon regularny | |
|---|---|
 Myriagon regularny
| |
| Typ | Regularny wielokąt |
| Krawędzie i wierzchołki | 10000 |
| Symbol Schläfliego | {10000}, t{5000}, tt{2500}, ttt{1250}, tttt{625} |
| Diagramy Coxetera-Dynkina |
|
| Grupa symetrii | Dwuścienny (D 10000 ), rząd 2 × 10000 |
| Kąt wewnętrzny ( stopnie ) | 179,964° |
| Nieruchomości | Wypukłe , cykliczne , równoboczne , izogonalne , izotoksalne |
| Podwójny wielokąt | Samego siebie |
W geometrii myriagon lub 10000-gon to wielokąt o 10000 bokach. Kilku filozofów użyło regularnego myriagonu, aby zilustrować kwestie dotyczące myśli.
Zwykły miriagon
Regularny myriagon jest reprezentowany przez symbol Schläfliego {10 000} i może być skonstruowany jako ścięty 5000-gon, t{5000} lub dwukrotnie ścięty 2500-gon, tt{2500} lub trzykrotnie ścięty 1250-gon , ttt{1250) lub czterokrotnie ścięte 625-gon, tttt{625}.
Miara każdego kąta wewnętrznego w miriabonie foremnym wynosi 179,964°. Pole miriakąta foremnego o bokach długości a jest określone wzorem
Wynik różni się od pola opisanego na nim okręgu nawet o 40 części na miliard .
Ponieważ 10 000 = 2 4 × 5 4 , liczba boków nie jest ani iloczynem różnych liczb pierwszych Fermata , ani potęgą dwójki. Tak więc regularny myriagon nie jest konstruowalnym wielokątem . Rzeczywiście, nie można go nawet skonstruować za pomocą trisektora kąta, ponieważ liczba boków nie jest ani iloczynem różnych liczb pierwszych Pierponta , ani iloczynem potęg dwóch i trzech.
Symetria
Regularny myriagon ma symetrię dwuścienną Dih 10000 , rząd 20000, reprezentowaną przez 10000 linii odbicia. Dih 10000 ma 24 dwuścienne podgrupy: (Dih 5000 , Dih 2500 , Dih 1250 , Dih 625 ), (Dih 2000 , Dih 1000 , Dih 500 , Dih 250 , Dih 125 ), (Dih 400 , Dih 200 , Dih 100 , Dih 50 , Dih 25 ), (Dh 80 , Dih 40 , Dih 20 , Dih 10 , Dih 5 ) i (Tri 16 , Dih 8 , Dih 4 , Dih 2 , Dih 1 ). Ma również 25 kolejnych cyklicznych jako podgrupy: (Z 10000 , Z 5000 , Z 2500 , Z 1250 , Z 625 ), (Z 2000 , Z 1000 , Z 500 , Z 250 , Z 125 ), (Z 400 , Z 200 , Z 100 , Z 50 , Z 25 ), (Z 80 , Z 40 , Z 20 , Z 10 ) i (Z 16 , Z 8 , Z 4 , Z 2 , Z 1 ), gdzie Zn reprezentujący π / n radianowej symetrii obrotowej.
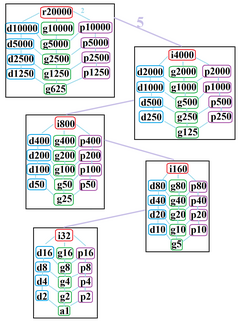
John Conway oznacza te niższe symetrie literą, a kolejność symetrii następuje po literze. r20000 reprezentuje pełną symetrię, a a1 oznacza brak symetrii. Podaje d (przekątną) z liniami lustrzanymi przechodzącymi przez wierzchołki, p z liniami lustrzanymi przechodzącymi przez krawędzie (prostopadłe), i z liniami lustrzanymi przechodzącymi przez wierzchołki i krawędzie oraz g dla symetrii obrotowej.
Te niższe symetrie pozwalają na stopniowanie swobody w definiowaniu nieregularnych myriagonów. Tylko g10000 nie ma stopni swobody, ale można ją postrzegać jako skierowane krawędzie .
Myriagram
Miriagram to gwiazda wielokątna o 10 000 bokach . Istnieje 1999 form regularnych podanych przez symbole Schläfliego postaci {10000/ n }, gdzie n jest liczbą całkowitą z przedziału od 2 do 5000, czyli względnie pierwszą do 10 000. W pozostałych przypadkach znajduje się również 3000 regularnych gwiazd .
W kulturze popularnej
W noweli Flatland zakłada się, że Główny Krąg ma dziesięć tysięcy boków, co czyni go myriagonem.