Twierdzenie Vivianiego

Dla dowolnego punktu wewnętrznego P suma długości s + u + t jest równa wysokości trójkąta równobocznego.

Twierdzenie Vivianiego , nazwane na cześć Vincenza Vivianiego , stwierdza, że ​​suma odległości od dowolnego punktu wewnętrznego do boków trójkąta równobocznego jest równa długości wysokości trójkąta . Jest to twierdzenie powszechnie stosowane w różnych konkursach matematycznych, egzaminach z matematyki w szkole średniej i ma szerokie zastosowanie do wielu problemów w świecie rzeczywistym.

Dowód

Wizualny dowód twierdzenia Vivianiego

1.	Pokazano najbliższe odległości od punktu P do boków trójkąta równobocznego ABC.
2.	Proste DE, FG i HI równoległe do odpowiednio AB, BC i CA i przechodzące przez P definiują podobne trójkąty PHE, PFI i PDG.
3.	Ponieważ te trójkąty są równoboczne, ich wysokości można obrócić tak, aby były pionowe.
4.	Ponieważ PGCH jest równoległobokiem, trójkąt PHE można przesunąć w górę, aby pokazać, że wysokości sumują się do wysokości trójkąta ABC.

Dowód ten opiera się na łatwym do udowodnienia twierdzeniu, że pole trójkąta to połowa jego podstawy razy jego wysokość — to znaczy połowa iloczynu jednego boku i wysokości z tego boku.

Niech ABC będzie trójkątem równobocznym o wysokości h i boku a .

Niech P będzie dowolnym punktem wewnątrz trójkąta, a u, s, t odległościami P od boków. Narysuj linię od P do każdego z A, B i C, tworząc trzy trójkąty PAB, PBC i PCA.

Teraz obszary tych trójkątów to ${\ Displaystyle {\ Frac {u \ cdot a} {2}}}$ , ${\ Displaystyle {\ Frac {s \ cdot a} {2}} }$ i ${\ Displaystyle {\ Frac {t \ cdot a} {2}}}$ . Dokładnie wypełniają otaczający trójkąt, więc suma tych pól jest równa polu otaczającego trójkąta. Możemy więc napisać:

${\ Displaystyle {\ Frac {u \ cdot a} {2}} + {\ Frac {s \ cdot a} {2}} + {\frac {t\cdot a}{2}}={\frac {h\cdot a}{2}}}$

a zatem

${\ Displaystyle u + s + t = h}$

CO BYŁO DO OKAZANIA

Rozmawiać

Zachodzi również sytuacja odwrotna: jeśli suma odległości od wewnętrznego punktu trójkąta do boków jest niezależna od położenia punktu, trójkąt jest równoboczny.

Aplikacje

Wykres palności metanu

Dalsze informacje: Działka trójdzielna

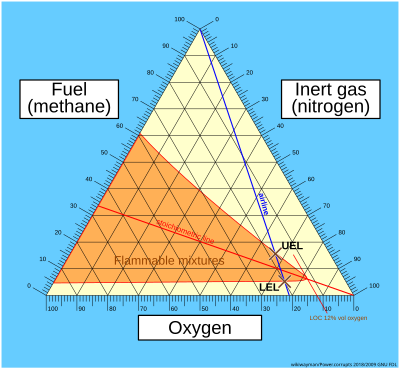
Twierdzenie Vivianiego oznacza, że ​​linie równoległe do boków trójkąta równobocznego dają współrzędne do tworzenia trójskładnikowych wykresów , takich jak diagramy palności .

Mówiąc bardziej ogólnie, pozwalają one podać współrzędne na zwykłym simpleksie w ten sam sposób.

Rozszerzenia

Równoległobok

Suma odległości od dowolnego punktu wewnętrznego równoległoboku do boków jest niezależna od położenia punktu. Zachodzi również sytuacja odwrotna: jeśli suma odległości od punktu we wnętrzu czworoboku do boków jest niezależna od położenia punktu, to czworobok jest równoległobokiem.

Wynik uogólnia się na dowolne 2 n -gon z przeciwległymi bokami równoległymi. Ponieważ suma odległości między dowolnymi parami przeciwległych boków równoległych jest stała, wynika z tego, że suma wszystkich sum parami między parami boków równoległych jest również stała. Generalnie odwrotność nie jest prawdziwa, ponieważ wynik odnosi się do równobocznego , który niekoniecznie ma przeciwległe boki równoległe.

Regularny wielokąt

Jeśli wielokąt jest regularny (zarówno równokątny, jak i równoboczny ), suma odległości do boków od punktu wewnętrznego jest niezależna od położenia tego punktu. W szczególności jest równy n -krotności apotemu , gdzie n to liczba boków, a apotem to odległość od środka do boku. Jednak sytuacja odwrotna nie zachodzi; równoległobok niekwadratowy jest kontrprzykładem .

Wielokąt równokątny

Suma odległości od punktu wewnętrznego do boków wielokąta równokątnego nie zależy od położenia punktu.

Wypukły wielokąt

Warunkiem koniecznym i wystarczającym, aby wielokąt wypukły miał stałą sumę odległości od dowolnego punktu wewnętrznego do boków, jest istnienie trzech niewspółliniowych punktów wewnętrznych o równych sumach odległości.

Regularny wielościan

Suma odległości od dowolnego punktu we wnętrzu wielościanu foremnego do boków jest niezależna od położenia punktu. Jednak sytuacja odwrotna nie zachodzi, nawet w przypadku czworościanów .

Dalsza lektura

•   Gueron, Shay; Tessler, Ran (2002). „Problem Fermata-Steinera”. Amer. Matematyka Miesięczny . 109 (5): 443–451. doi : 10.2307/2695644 . JSTOR 2695644 .
•   Samelson, Hans (2003). „Dowód bez słów: twierdzenie Vivianiego z wektorami”. Matematyka Mag . 76 (3): 225. doi : 10.2307/3219327 . JSTOR 3219327 .
•   Chen, Zhibo; Liang, Tian (2006). „Odwrotność twierdzenia Vivianiego”. Dziennik Matematyki Kolegium . 37 (5): 390–391. doi : 10.2307/27646392 . JSTOR 27646392 .
•    Kawasaki, Ken-Ichiroh; Yagi, Yoshihiro; Yanagawa, Katsuya (2005). „O twierdzeniu Vivianiego w trzech wymiarach”. Matematyka Gaz . 89 (515): 283–287. doi : 10.1017/S002555720017785X . JSTOR 3621243 . S2CID 126113074 .
•    Zhou, Li (2012). „Polytopy Vivianiego i punkty Fermata”. kol. Matematyka J. _ 43 (4): 309–312. ar Xiv : 1008.1236 . CiteSeerX 10.1.1.740.7670 . doi : 10.4169/college.math.j.43.4.309 . S2CID 117039483 .

Linki zewnętrzne

• Weisstein, Eric W. „Twierdzenie Vivianiego” . MathWorld .
• Li Zhou, Viviani Polytopes i Punkty Fermata
• „Twierdzenie Vivianiego: co to jest?” . w Przetnij węzeł .
• Warendorff, Jay. „Twierdzenie Vivianiego” . projekt demonstracji Wolframa .
• „Odmiana twierdzenia Vivianiego i niektóre uogólnienia” . w Dynamiczne szkice geometrii , interaktywny szkic dynamicznej geometrii.
• Abboud, Eliasz (2017). „Loci punktów inspirowane twierdzeniem Vivianiego”. arXiv : 1701,07339 [ matematyka.HO ].
• Armstrong, Addie; McQuillan, Dan (2017). „Specjalizacja, uogólnienie i nowy dowód twierdzenia Vivianiego”. arXiv : 1701.01344 [ matematyka.HO ].