Małe gwiaździste 120-ogniwowe
| Mała gwiaździsta 120-komorowa | |
|---|---|
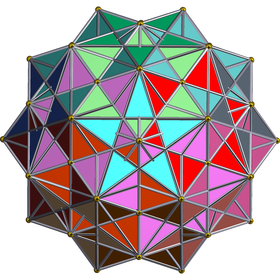 projekcja ortogonalna |
|
| Typ | Schläfli-Hess polytope |
| Komórki | 120 {5/2,5} |
| Twarze | 720 {5/2} |
| Krawędzie | 1200 |
| Wierzchołki | 120 |
| figura wierzchołka | {5,3} |
| Symbol Schläfliego | {5/2,5,3} |
| Diagram Coxetera-Dynkina |
|
| Grupa symetrii | H4 , [3,3,5] |
| Podwójny | Dwudziestościenny 120 komórek |
| Nieruchomości | Regularny |
W geometrii mały gwiaździsty 120-komorowy lub gwiaździsty polidodekahedron jest zwykłą gwiazdą 4-politopową z symbolem Schläfliego {5/2,5,3}. Jest to jeden z 10 regularnych polytopów Schläfli-Hess .
Powiązane polytopy
Ma taki sam układ krawędzi jak wielki wielki 120-komórkowy , a także dzieli swoje 120 wierzchołków z 600-komórkowym i ośmioma innymi regularnymi gwiazdami 4-politopami. Może być również postrzegana jako pierwsza gwiazda 120-ogniw. W tym sensie można go postrzegać jako analogię do trójwymiarowego małego dwunastościanu gwiaździstego , który jest pierwszą gwiazdą dwunastościanu . Rzeczywiście, mała gwiaździsta komórka 120 jest podwójna w stosunku do dwudziestościennej komórki 120 , którą można uznać za analog 4D dwunastościan wielki , podwójny z dwunastościanu małego gwiaździstego.
Krawędzie małych gwiaździstych 120 komórek mają τ 2 tak długo, jak krawędzie rdzenia 120 komórek wewnątrz 4-polytopu.
| H 3 | ZA 2 / B 3 / R 4 | A 3 / B 2 |
|---|---|---|

|

|

|
Zobacz też
- Lista regularnych polytopów
- Wypukły regularny 4-polytop - Zestaw wypukłych regularnych 4-polytope
- Bryły Keplera-Poinsota - wielościan gwiazdy foremnej
- Gwiazda wielokąta - regularne wielokąty gwiazdy
- Edmund Hess , (1883) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder [1] .
- HSM Coxeter , Regularne Polytopy , 3. red., Dover Publications, 1973. ISBN 0-486-61480-8 .
- John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Rozdział 26, Regular Star-polytopes, s. 404–408)
- Klitzing, Richard. "4D jednolite politopy (polichora) o3o5o5/2x - sishi" .
Linki zewnętrzne
- Zwykła polichora
- Dyskusja na temat imion
- Regulowany Polytope
- Regularna gwiazda Polychora
- Zome Model ostatecznej stellacji 120 komórek
- Pierwsza gwiazda 120-ogniwowego modelu Zome