Złożony wykres kostki
| Wykres kostki złożonej | |
|---|---|
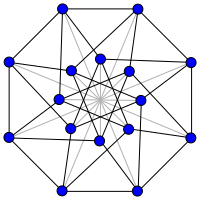 Wykres kostki złożonej w wymiarze 5 (tj. wykres Clebscha ).
| |
| Wierzchołki | 2 n −1 |
| Krawędzie | 2 n −2 rz |
| Średnica | podłoga ( n /2) |
| Liczba chromatyczna | 2 (dla parzystych n ) lub 4 (gdy nieparzyste). |
| Nieruchomości |
Graf regularny Hamiltonian Odległość przechodnia . |
| Tabela wykresów i parametrów | |
W teorii grafów złożony graf sześcienny jest grafem nieskierowanym utworzonym z wykresu hipersześcianu przez dodanie do niego idealnego dopasowania , które łączy przeciwległe pary wierzchołków hipersześcianu.
Budowa
Złożony wykres sześcienny o wymiarze k (zawierający 2 k - 1 wierzchołki) można utworzyć przez dodanie krawędzi między przeciwległymi parami wierzchołków w grafie hipersześcianu o wymiarze k - 1. (W hipersześcianie z 2 n wierzchołkami para wierzchołków to przeciwnie, jeśli najkrótsza ścieżka między nimi ma długość n .) Można go równoważnie utworzyć z wykresu hipersześcianu (również) o wymiarze k , który ma dwa razy więcej wierzchołków, identyfikując razem (lub skracając) każdą przeciwległą parę wierzchołków.
Nieruchomości
wymiarach k jest k - regularny z 2 k - 1 wierzchołkami i 2 k - 2 k krawędzi.
Liczba chromatyczna wykresu kostki złożonej wymiaru k wynosi dwa, gdy k jest parzyste (czyli w tym przypadku wykres jest dwudzielny ) i cztery, gdy k jest nieparzyste. Nieparzysty obwód złożonego sześcianu o nieparzystym wymiarze wynosi k , więc dla nieparzystego k większego niż trzy grafy złożonego sześcianu zapewniają klasę grafów bez trójkątów z chromatyczną liczbą cztery i dowolnie dużym nieparzystym obwodem. Jako wykres regularny odległości o nieparzystym obwodzie k i średnicy ( k - 1)/2, złożone sześciany o nieparzystym wymiarze są przykładami uogólnionych wykresów nieparzystych .
Gdy k jest nieparzyste, dwudzielna podwójna osłona złożonego sześcianu o wymiarze k jest sześcianem o wymiarze k , z którego została utworzona. Jednak gdy k jest parzyste, sześcian o wymiarze k jest podwójnym pokryciem , ale nie dwudzielnym podwójnym pokryciem. W tym przypadku złożony sześcian sam w sobie jest już dwudzielny . Złożone grafy sześcienne dziedziczą po swoich podgrafach hipersześcianu właściwość posiadania cyklu Hamiltona , a od hipersześcianów, które je podwójnie pokrywają, właściwość bycia grafem przechodnim na odległość .
Gdy k jest nieparzyste, zagięty sześcian wymiaru k zawiera jako podgraf kompletne drzewo binarne z 2 k - 1 węzłami. Jednak gdy k jest parzyste, nie jest to możliwe, ponieważ w tym przypadku złożony sześcian jest grafem dwudzielnym z równą liczbą wierzchołków po każdej stronie dwupodziału, bardzo różniącym się od stosunku prawie dwa do jednego dla dwupodziału pełne drzewo binarne.
Przykłady
- Graf złożonej kostki wymiaru trzeciego jest grafem pełnym K 4 .
- Graf złożonej kostki o wymiarze czwartym jest kompletnym grafem dwudzielnym K 4,4 .
- Graf złożonej kostki wymiaru piątego to wykres Clebscha .
- Graf złożonej kostki wymiaru szóstego to wykres Kummera, tj. wykres Leviego konfiguracji płaszczyzny punktowej Kummera .
Aplikacje
W obliczeniach równoległych grafy złożonych kostek były badane jako potencjalna topologia sieci , jako alternatywa dla hipersześcianu. W porównaniu z hipersześcianem , złożony sześcian z taką samą liczbą wierzchołków ma prawie taki sam stopień wierzchołków, ale tylko połowę średnicy . Wydajne algorytmy rozproszone (w porównaniu z algorytmami hipersześcianu ) są znane z rozgłaszania informacji w złożonej kostce.
Zobacz też
Notatki
- van Bon, John (2007), „Skończone prymitywne grafy przechodnie odległości”, European Journal of Combinatorics , 28 (2): 517–532, doi : 10.1016/j.ejc.2005.04.014 .
- Choudam, SA; Nandini, R. Usha (2004), „Kompletne drzewa binarne w złożonych i ulepszonych kostkach”, Networks , 43 (4): 266–272, doi : 10.1002/net.20002 .
- Van Dam, Edwin; Haemers, Willem H. (2010), Nieparzysta charakterystyka uogólnionych wykresów nieparzystych , seria dokumentów dyskusyjnych Centrum nr 2010-47, SSRN 1596575 .
- El-Amawy, A.; Latifi, S. (1991), „Właściwości i działanie złożonych hipersześcianów”, IEEE Trans. Dystrybucja równoległa. Syst. , 2 (1): 31–42, doi : 10.1109/71.80187 .
- Godsil, Chris (2004), Ciekawe wykresy i ich kolorowanie , CiteSeerX 10.1.1.91.6390 .
- Varvarigos, E. (1995), „Wydajne algorytmy routingu dla sieci składanych sześcianów”, Proc. 14. Int. Konf. Phoenix w sprawie komputerów i komunikacji , IEEE, s. 143–151, doi : 10.1109/PCCC.1995.472498 .