Rektyfikowane 7-ortopleksy

7-ortopleks	Rektyfikowany 7-ortopleks	Birektyfikowany 7-ortopleks	Trirektyfikowany 7-ortopleks
Birektyfikowana 7-kostka	Rektyfikowana 7-kostka	7-sześcian
Rzuty ortogonalne w płaszczyźnie B 7 Coxetera

W siedmiowymiarowej geometrii rektyfikowany 7-ortopleks jest wypukłym jednolitym 7-politopem , będącym rektyfikacją regularnego 7-ortopleksu .

Istnieje 7 unikalnych stopni rektyfikacji, zerowy to 7-ortopleks , a szósty i ostatni to 7-sześcian . Wierzchołki rektyfikowanego 7-ortopleksu znajdują się w środkach krawędzi 7-ortopleksu. Wierzchołki birektyfikowanego 7-ortopleksu znajdują się w trójkątnych środkach twarzy 7-ortopleksu. Wierzchołki trirektyfikowanego 7-ortopleksu znajdują się w czworościennych centrach komórek 7-ortopleksu.

Rektyfikowany 7-ortopleks

Rektyfikowany 7-ortopleks
Typ	jednolity 7-politop
Symbol Schläfliego	r{3,3,3,3,3,4}
Diagramy Coxetera-Dynkina
6-twarzy	142
5 twarzy	1344
4 twarze	3360
Komórki	3920
Twarze	2520
Krawędzie	840
Wierzchołki	84
figura wierzchołka	Pryzmat 5-ortopleksowy
grupy Coxetera	B 7 , [3,3,3,3,3,4] D 7 , [3 4,1,1 ]
Nieruchomości	wypukły

Zrektyfikowany 7-ortopleks jest figurą wierzchołka demihepteraktycznego plastra miodu . 84 wierzchołki rektyfikowanego 7-ortopleksu reprezentują liczbę pocałunków opakowania sferycznego zbudowanego z tego plastra miodu.

Lub

Alternatywne nazwy

• siedmiokrzyżowy rektyfikowany
• rektyfikowany hecatonicosoctaexon (akronim rez) (Jonathan Bowers) - rektyfikowany poliekson 128-płaszczyznowy

Obrazy

rzuty ortograficzne

Samolot Coxetera	B 7 / A 6	B 6 / D 7	B 5 / R 6 / A 4
Wykres
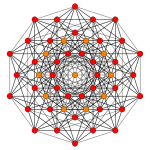
Symetria dwuścienna	[14]	[12]	[10]
Samolot Coxetera	B 4 / D 5	B 3 / R 4 / A 2	B2 / D3 _
Wykres
Symetria dwuścienna	[8]	[6]	[4]
Samolot Coxetera	5 _	3 _
Wykres
Symetria dwuścienna	[6]	[4]

Budowa

Istnieją dwie grupy Coxetera związane z rektyfikowanym heptacrossem , jedna z grupą C ₇ lub [4,3,3,3,3,3] Coxeter, oraz niższa symetria z dwiema kopiami ścian pentacrossowych, naprzemiennie, z D ₇ lub [3 ^4,1,1 ] grupa Coxetera.

współrzędne kartezjańskie

Współrzędne kartezjańskie wierzchołków wyprostowanego heptacrossu, wyśrodkowane w początku, długość krawędzi są permutacjami: ${\ Displaystyle {\ sqrt {2}} \}$

(±1,±1,0,0,0,0,0)

Wektory korzeniowe

_{reprezentują} wektory pierwiastków prostej grupy Liego D7 . Wierzchołki można zobaczyć w 3 hiperpłaszczyznach , z 21 wierzchołkami rektyfikowanymi komórkami 6-simplex po przeciwnych stronach i 42 wierzchołkami rozszerzonego 6-simpleksu przechodzącego przez środek. W połączeniu z 14 wierzchołkami ortopleksu 7, wierzchołki te reprezentują 98 wektorów korzeni prostych grup Liego _B7 i C7 _.

Birektyfikowany 7-ortopleks

Birektyfikowany 7-ortopleks
Typ	jednolity 7-politop
Symbol Schläfliego	2r{3,3,3,3,3,4}
Diagramy Coxetera-Dynkina
6-twarzy	142
5 twarzy	1428
4 twarze	6048
Komórki	10640
Twarze	8960
Krawędzie	3360
Wierzchołki	280
figura wierzchołka	{3}×{3,3,4}
grupy Coxetera	B 7 , [3,3,3,3,3,4] D 7 , [3 4,1,1 ]
Nieruchomości	wypukły

Alternatywne nazwy

• Heptacross z birektyfikacją
• Birektyfikowany hecatonicosoctaexon (akronim barz) (Jonathan Bowers) - birektyfikowany 128-płaszczyznowy poliekson

Obrazy

rzuty ortograficzne

Samolot Coxetera	B 7 / A 6	B 6 / D 7	B 5 / R 6 / A 4
Wykres
Symetria dwuścienna	[14]	[12]	[10]
Samolot Coxetera	B 4 / D 5	B 3 / R 4 / A 2	B2 / D3 _
Wykres
Symetria dwuścienna	[8]	[6]	[4]
Samolot Coxetera	5 _	3 _
Wykres
Symetria dwuścienna	[6]	[4]

współrzędne kartezjańskie

Współrzędne kartezjańskie dla wierzchołków birektyfikowanego 7-ortopleksu, wyśrodkowane w początku, długość krawędzi są permutacjami: ${\ Displaystyle {\ sqrt {2}} \}$

(±1,±1,±1,0,0,0,0)

Trirektyfikowany 7-ortopleks

Trirektyfikowany 7-ortopleks jest tym samym, co trirektyfikowany 7-sześcian .

Notatki

• HSM Coxeter :
  • HSM Coxeter, Regularne Polytopes , wydanie 3, Dover, Nowy Jork, 1973
  •   Kaleidoscopes: Selected Writings of HSM Coxeter , pod redakcją F. Arthura Sherka, Petera McMullena, Anthony'ego C. Thompsona, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Papier 22) HSM Coxeter, Regularne i półregularne Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Papier 23) HSM Coxeter, Regularne i półregularne Polytopes II , [Math. Zeit. 188 (1985) 559-591]
    • (Papier 24) HSM Coxeter, Regularne i półregularne Polytopy III , [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes , Rękopis (1991)
  • NW Johnson: Theory of Uniform Polytopes and Honeycombs , Ph.D.
• Klitzing, Richard. „Jednolite polytopy 7D (poliexa)” . o3x3o3o3o3o4o - rez, o3o3x3o3o3o4o - barz

Linki zewnętrzne

• Polytopy o różnych wymiarach
• Słowniczek wielowymiarowy