Permutoedr

Permutoedr rzędu 4

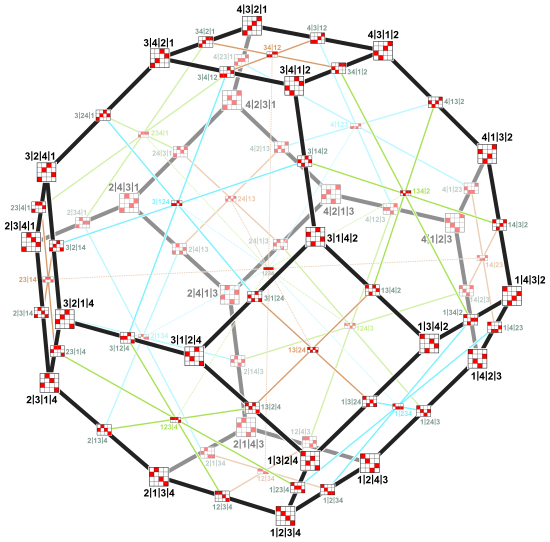
W matematyce permutoedr rzędu n jest ( n - 1)-wymiarowym polytopem osadzonym w n - wymiarowej przestrzeni. Jego wierzchołków (etykiety) są permutacjami pierwszych n liczb naturalnych . Krawędzie identyfikują najkrótsze możliwe ścieżki (zbiory transpozycji ), które łączą dwa wierzchołki (permutacje). Dwie permutacje połączone krawędzią różnią się tylko w dwóch miejscach (jedna transpozycja ), a liczby na tych miejscach są sąsiadami (różnią się wartością o 1).

Obraz po prawej stronie przedstawia permutoedr rzędu 4, który jest ściętym ośmiościanem . Jego wierzchołki to 24 permutacje (1, 2, 3, 4). Krawędzie równoległe mają ten sam kolor krawędzi. 6 kolorów krawędzi odpowiada 6 możliwym transpozycjom 4 elementów, czyli wskazuje, w których dwóch miejscach różnią się połączone permutacje. (Np. czerwone krawędzie łączą permutacje różniące się w dwóch ostatnich miejscach.)

Historia

Według Güntera M. Zieglera ( 1995 ), permutoedry zostały po raz pierwszy zbadane przez Pietera Hendrika Schoute ( 1911 ). Nazwa permutoèdre została ukuta przez Georgesa Th. Guilbaud i Pierre Rosenstiehl ( 1963 ). Określają to słowo jako barbarzyńskie, ale łatwe do zapamiętania i poddają je krytyce swoich czytelników.

Czasami używana jest również alternatywna pisownia permut a hedron . Permutoedry są czasami nazywane politopami permutacyjnymi , ale ta terminologia jest również używana w odniesieniu do pokrewnego polytopu Birkhoffa , definiowanego jako wypukła powłoka macierzy permutacyjnych . Mówiąc bardziej ogólnie, V. Joseph Bowman ( 1972 ) używa tego terminu dla dowolnego polytopu, którego wierzchołki mają bijekcję z permutacjami jakiegoś zbioru.

Wierzchołki, krawędzie i fasetki

wierzchołki , krawędzie , ścianki , ściany Wymiar ściany d = n − k .

k = 1 2 3 4 5 n 1 1 1 2 1 2 3 3 1 6 6 13 4 1 14 36 24 75 5 1 30 150 240 120 541

Permutoedr rzędu n ma n ! wierzchołki, z których każdy sąsiaduje z n - 1 innymi. Liczba krawędzi wynosi ( n − 1) n ! / 2 , a ich długość to √ 2 .

Dwa połączone wierzchołki różnią się zamianą dwóch współrzędnych, których wartości różnią się o 1. Para zamienionych miejsc odpowiada kierunkowi krawędzi. (Na przykładowym obrazie wierzchołki (3, 2, 1, 4) i (2, 3, 1, 4) są połączone niebieską krawędzią i różnią się zamianą 2 i 3 na pierwszych dwóch miejscach. Wartości 2 i 3 różnią się o 1. Wszystkie niebieskie krawędzie odpowiadają zamianie współrzędnych na pierwszych dwóch miejscach.)

Liczba aspektów wynosi 2 ⁿ − 2 , ponieważ odpowiadają one niepustym właściwym podzbiorom S z {1 ... n } . Wspólną cechą wierzchołków fasetki odpowiadającej podzbiorowi S jest to, że ich współrzędne w miejscach w S są mniejsze niż pozostałe .

Przykłady aspektów
Dla rzędu 3 ścianki to 6 krawędzi, a dla rzędu 4 to 14 ścian . Współrzędne miejsc i, gdzie i ∈ S zaznaczono ciemnym tłem. Widać, że są mniejsze od pozostałych. Kwadrat na górze odpowiada podzbiorowi {3, 4} . W jej czterech wierzchołkach współrzędne dwóch ostatnich miejsc mają najmniejsze wartości (czyli 1 i 2).
zamówienie 3		zamówienie 4
Podzbiory 1-elementowe	Podzbiory 2-elementowe	Podzbiory 1-elementowe	Podzbiory 2-elementowe	podzbiory 3-elementowe

Mówiąc bardziej ogólnie, ściany o wymiarach od 0 (wierzchołki) do n - 1 (sam permutoedr) odpowiadają ściśle słabym uporządkowaniom zbioru {1 ... n } . Zatem liczba wszystkich ścian jest n - tą uporządkowaną liczbą Bella . Ściana o wymiarze d odpowiada uporządkowaniu z k = n - d klasami równoważności.

Przykłady twarzy
zamówienie 3	zamówienie 4
Powyższe obrazy przedstawiają kraty ścian permutoedrów rzędu 3 i 4 (bez pustych ścian) . Każde centrum twarzy jest oznaczone ściśle słabym uporządkowaniem. Np. kwadrat na górze jako 3 4 | 1 2 , co reprezentuje ({3, 4}, {1, 2}) . Porządki są częściowo uporządkowane według wyrafinowania , przy czym te drobniejsze znajdują się na zewnątrz. Przesuwanie się wzdłuż krawędzi do wewnątrz oznacza łączenie dwóch sąsiednich klas równoważności. Wierzchołek oznacza | b | c | d interpretowane jako permutacje (a, b, c, d) to te, które tworzą wykres Cayleya. Fasety wśród twarzy Wspomniane wcześniej fasetki należą do tych ścian i odpowiadają uporządkowaniom z dwiema klasami równoważności. Pierwszy jest używany jako podzbiór S przypisany do aspektu, więc kolejność to ( S , S c ) . Poniższe obrazy pokazują, w jaki sposób ścianki permutoedru n odpowiadają prostemu rzutowi n - sześcianu . Etykiety współrzędnych binarnych odpowiadają podzbiorom S , np. od 0011 do {3, 4} . (Wierzchołek rzutowany na środek nie odpowiada ściance. Ani też jego przeciwny wierzchołek w n -sześcianie, który nie jest częścią rzutu).

Liczba ścian o wymiarze d = n - k w permutoedrze rzędu n jest dana trójkątem T (sekwencja A019538 w OEIS ): ${\ Displaystyle T (n, k) = k! \ cdot \ lewo \ {{n \ na szczycie k} \ prawo \}}$ z ${\ displaystyle \ textstyle \ lewo \ {{n \ na szczycie k} \ prawo \}}$ reprezentujące liczby Stirlinga drugiego rodzaju Jest to pokazane po prawej stronie wraz z sumami wierszy, uporządkowanymi liczbami Bella .

Inne właściwości

Podobny do permutoedru wykres Cayleya S ₄ (patrz tutaj porównanie z permutoedrem)

Permutoedr jest wierzchołkowo-przechodni : grupa symetryczna S _n działa na permutoedr poprzez permutację współrzędnych.

Permutoedr jest zonotopem ; przetłumaczoną kopię permutoedru można wygenerować jako sumę ( n - 1)/2 Minkowskiego n odcinków łączących pary standardowych wektorów bazowych .

Wierzchołki i krawędzie permutoedru są izomorficzne z jednym z grafów Cayleya grupy symetrycznej , czyli generowanym przez transpozycje zamieniające kolejne elementy. Wierzchołki wykresu Cayleya są odwrotnymi permutacjami tych w permutoedrze. Obraz po prawej pokazuje wykres Cayleya dla S 4 . Kolory jego krawędzi reprezentują 3 generujące transpozycje: (1, 2) , (2, 3) , (3, 4)

Ten graf Cayleya jest hamiltonowski ; cykl Hamiltona można znaleźć za pomocą algorytmu Steinhausa – Johnsona – Trottera .

Teselacja przestrzeni

Teselacja przestrzeni przez permutoedry rzędów 3 i 4

Permutoedr rzędu n leży całkowicie w ( n - 1 ) - wymiarowej hiperpłaszczyźnie składającej się ze wszystkich punktów, których współrzędne sumują się do liczby

1 + 2 + ... + n = n ( n + 1)/2.

Co więcej, ta hiperpłaszczyzna może być wyłożona nieskończenie wieloma przetłumaczonymi kopiami permutoedru. Każdy z nich różni się od podstawowego permutoedru elementem pewnej ( n − 1)-wymiarowej sieci , która składa się z n -krotek liczb całkowitych, których suma wynosi zero i których reszty (modulo n ) są równe:

x ₁ + x ₂ + ... + x _n = 0

x ₁ ≡ x ₂ ≡ ... ≡ x _n (mod n ).

korzeniowej $n-1$ krata , podwójna krata sieci ZA $1 {$ Innymi słowy, permutoedr jest komórką Woronoja dla ${\ Displaystyle A_ {n-1} ^ {*}}$ . W związku z tym ta sieć jest czasami nazywana siecią permutoedryczną.

Zatem permutoedr rzędu 4 pokazany powyżej układa trójwymiarową przestrzeń przez translację. Tutaj przestrzeń trójwymiarowa jest podprzestrzenią afiniczną przestrzeni czterowymiarowej R ⁴ o współrzędnych x , y , z , w która składa się z 4-krotek liczb rzeczywistych, których suma wynosi 10,

x + y + z + w = ​​10.

Można łatwo sprawdzić, że dla każdego z następujących czterech wektorów

(1,1,1,-3), (1,1,-3,1), (1,-3,1,1) i (-3,1,1,1),

suma współrzędnych wynosi zero, a wszystkie współrzędne są zgodne z 1 (mod 4). Dowolne trzy z tych wektorów generują siatkę translacji.

Teselacje utworzone w ten sposób z permutoedrów rzędu 2, rzędu 3 i rzędu 4 to apeirogon , regularne sześciokątne kafelki i sześcienny plaster miodu z bitami . Podwójne teselacje zawierają wszystkie simplex , chociaż nie są regularnymi polytopami poza rzędem-3.

Przykłady

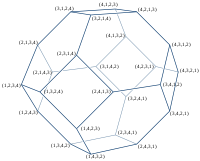
Zamówienie 2	Zamówienie 3	Zamówienie 4	Zamówienie 5	Zamówienie 6
2 wierzchołki	6 wierzchołków	24 wierzchołki	120 wierzchołków	720 wierzchołków
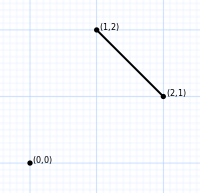
odcinek	sześciokąt	ścięty ośmiościan	omnitruncated 5-cell	omnitruncated 5-simplex

Zobacz też

• Skojarzony
• cyklohedron
• Permutoasocjaścian

Notatki

•   Baek, Jongmin; Adams, Andrzej; Dolson, Jennifer (2013), „Wielkowymiarowe filtrowanie gaussowskie oparte na sieci i siatka permutoedryczna”, Journal of Mathematical Imaging and Vision , 46 (2): 211–237, doi : 10.1007/s10851-012-0379-2 , hdl : 1721.1/105344 , MR 3061550
•    Bowman, V. Joseph (1972), „Permutacja wielościanów”, SIAM Journal on Applied Mathematics , 22 (4): 580–589, doi : 10.1137/0122054 , JSTOR 2099695 , MR 0305800 .
•    Gaiha, Prabha; Gupta, SK (1977), „Sąsiednie wierzchołki na permutoedrze”, SIAM Journal on Applied Mathematics , 32 (2): 323–327, doi : 10.1137/0132025 , JSTOR 2100417 , MR 0427102 .
• Guilbaud, Georges Th.; Rosenstiehl, Pierre (1963), „Analiza algébrique d'un scrutin” , Mathématiques et Sciences Humaines , 4 : 9–33 .
•   Lancia, Giuseppe (2018), Kompaktowe rozszerzone modele programowania liniowego , Cham, Szwajcaria: Springer, ISBN 978-3-319-63975-8 .
• Schoute, Pieter Hendrik (1911), „Analityczne traktowanie polytopes regularnie wywodzących się z regularnych polytopes”, Verhandelingen der Koninklijke Akademie van Wetenschappen Te Amsterdam , 11 (3): 87 pp Googlebook, 370–381 Również online w Bibliotece Cyfrowej KNAW pod adresem http://www.dwc.knaw.nl/toegangen/digital-library-knaw/?pagetype=publDetail&pId=PU00011495
•   Thomas, Rekha R. (2006), „Rozdział 9. Permutahedron”, Wykłady z kombinatoryki geometrycznej , Student Mathematical Library: IAS / Park City Mathematical Subseries, tom. 33, Amerykańskie Towarzystwo Matematyczne , s. 85–92, ISBN 978-0-8218-4140-2 .
• Ziegler, Günter M. (1995), Lectures on Polytopes , Springer-Verlag, Graduate Texts in Mathematics 152 .

Dalsza lektura

• Le Conte de Poly-Barbut, kl. (1990), "Le diagramme du treillis permutoèdre est skrzyżowanie des diagrammes de deux produits directs d'ordres totaux", Mathématiques, Informatique et Sciences Humaines , 112 : 49–53 .
•   Postnikov, Alexander (2009), „Permutohedra, associahedra and Beyond”, Międzynarodowe uwagi badawcze z matematyki (6): 1026–1106, arXiv : math.CO/0507163 , doi : 10.1093/imrn/rnn153 , MR 2487491
• Santmyer, Joe (2007), „Dla wszystkich możliwych odległości spójrz na permutohedron”, Mathematics Magazine , 80 (2): 120–125, doi : 10,1080/0025570X.2007.11953465

Linki zewnętrzne

• Bryan Jacobs, „Permutoedr” , MathWorld