Konstrukcja Goldberga-Coxetera

Wielościan Goldberga (3,1) i wielościan geodezyjny (3,1). Wielościany Goldberga i wielościany geodezyjne były prekursorami operacji Goldberga-Coxetera.

Konstrukcja Goldberga – Coxetera lub operacja Goldberga – Coxetera ( konstrukcja GC lub operacja GC ) to operacja grafowa zdefiniowana na regularnych grafach wielościennych o stopniu 3 lub 4. Dotyczy to również wykresu dualnego owych grafów, tj. grafów o trójkątnych lub czworobocznych "ścianach". Konstrukcję GC można traktować jako podzielenie ścian wielościanu za pomocą siatki trójkątnych, kwadratowych lub sześciokątnych wielokątów, prawdopodobnie skośnych w stosunku do pierwotnej ściany: jest to rozszerzenie koncepcji wprowadzonych przez wielościany Goldberga i wielościany geodezyjne . Konstrukcja GC jest badana głównie w chemii organicznej pod kątem zastosowania do fulerenów , ale została zastosowana do nanocząstek , projektowania wspomaganego komputerowo , wyplatanie koszy oraz ogólne studium teorii grafów i wielościanów .

Konstrukcję Goldberga-Coxetera można oznaczyć jako , gdzie jest obsługiwanym wykresem $)}$ $G_ {0}$ $}$ , i są $\$ całkowitymi, $Displaystyle k> 0}$ i ${\ Displaystyle \ ell \ geq 0$ .

Historia

Michael Goldberg przedstawił wielościan Goldberga w 1937 roku. Buckminster Fuller ukuł termin „ kopuła geodezyjna ” w latach czterdziestych XX wieku, chociaż w dużej mierze utrzymywał matematykę kryjącą się za kopułami w tajemnicy handlowej. Kopuły geodezyjne są geometryczną liczbą podwójną (części) wielościanu Goldberga: pełną kopułę geodezyjną można traktować jako wielościan geodezyjny , podwójny w stosunku do wielościanu Goldberga. W 1962 roku Donald Caspar i Aaron Klug opublikowali artykuł na temat geometrii kapsydów wirusowych który zastosował i rozszerzył koncepcje Goldberga i Fullera. HSM Coxeter opublikował artykuł w 1971 roku obejmujący wiele z tych samych informacji. Caspar i Klug jako pierwsi opublikowali najbardziej ogólną poprawną konstrukcję wielościanu geodezyjnego, czyniąc nazwę „konstrukcja Goldberga-Coxetera” przykładem prawa eponimii Stiglera .

Odkrycie Buckminsterfullerene w 1985 roku zmotywowało do badań nad innymi cząsteczkami o strukturze wielościanu Goldberga. Terminy „fulereny Goldberga – Coxetera” i „konstrukcja Goldberga – Coxetera” zostały wprowadzone przez Michela Dezę w 2000 r. Jest to również pierwszy raz, kiedy rozważano przypadek stopnia 4.

Budowa

Ta sekcja jest w dużej mierze zgodna z dwoma artykułami Dezy i wsp.

Mistrzowskie wielokąty

Kraty
n-Regularny	3	4
Domena	Eisensteina ${\ displaystyle a + bu}$	gaussowski ${\ displaystyle a + bi}$
Przylegająca jednostka	${\ Displaystyle {\ rozpocząć {wyrównane} u & = {\ Frac {1} {2}} \ lewo (1 + i {\ sqrt {3}}\right)\\&=e^{{\frac {1}{3}}\pi i}=\omega +1\end{wyrównane}}}$	${\ Displaystyle i = {\ sqrt {-1}}}$
Norma ${\ Displaystyle t (a, b)}$	${\ Displaystyle a ^ {2} + ab + b ^ {2}}$	${\ Displaystyle a ^ {2} + b ^ {2}}$ .
Główny wielokąt	${\ Displaystyle (0, x, xu)}$	${\ Displaystyle (0, x, x (1 + ja), xi)}$

Regularne kraty na płaszczyźnie zespolonej mogą być używane do tworzenia „głównych wielokątów”. W terminologii kopuł geodezyjnych jest to „struktura podziału” lub „główny trójkąt wielościenny” (PPT). Przypadek 4-regularny wykorzystuje siatkę kwadratową na liczbach całkowitych Gaussa , a przypadek 3-regularny wykorzystuje siatkę trójkątną na liczbach całkowitych Eisensteina . Dla wygody zastosowano alternatywną parametryzację liczb całkowitych Eisensteina, opartą na szóstym pierwiastku jedności zamiast trzeciego. Zwykła definicja liczb całkowitych Eisensteina wykorzystuje element ${\ textstyle \ omega = {\ Frac {1} {2}} \ lewo (-1 + i {\ sqrt {3}} \ prawo) =e^{{\frac {2}{3}}\pi i}=u-1}$ . Norma $kwadrat$ bezwzględnej liczby W przypadku wykresów 3-regularnych normą tą jest liczba T lub liczba triangulacji stosowana w wirusologii.

Główny wielokąt to równoboczny trójkąt lub kwadrat ułożony na siatce. Tabela po prawej stronie zawiera wzory na wierzchołki głównych wielokątów na płaszczyźnie zespolonej, a poniższa galeria przedstawia główny trójkąt i kwadrat (3,2). $y}$ wiele liczb, które mogą opisywać ten sam wielokąt: są one ze sobą powiązane: if i y $x}$ $displaystyle$ są towarzyszami, to ${$ $}$ w Eisensteinach lub Gaussach dla pewnej liczby całkowitej $n}$ . Zbiór elementów, które są ze sobą powiązane, jest $klasą$ równoważności , a element każdej klasy równoważności $który$ jest postacią .

(3,2) główny trójkąt nad trójkątną siatką
(3,2) główny kwadrat nad kwadratową siatką

Główne wielokąty i operator można sklasyfikować w następujący sposób: ${\ Displaystyle GC_ {k, \ ell} \ lewo (G_ {0} \ right)}$

Klasa I: ${\ Displaystyle \ ell = 0.}$
Klasa II: ${\ displaystyle k = \ ell.}$
Klasa III: wszystkie inne. Operatory klasy III istnieją w parach chiralnych: ${\ Displaystyle GC_ {k, \ ell} \ lewo (G_ {0} \ prawej)}$ to chiralna para ${\ Displaystyle GC_ {\ ell, k} (G_ {0})}$ .

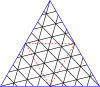
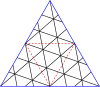
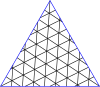
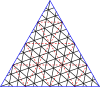
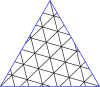
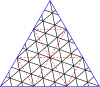
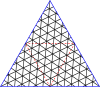
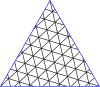
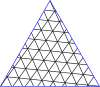
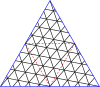
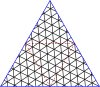
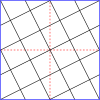
Poniżej znajdują się tabele głównych trójkątów i kwadratów. Klasa I odpowiada pierwszej kolumnie, a klasa II odpowiada przekątnej z nieco ciemniejszym tłem.

Mistrzowskie wielokąty dla trójkątów

Opanuj trójkąty do (8,8)
	0	1	2	3	4	5	6	7	8
1
2
3
4
5
6
7
8

Mistrzowskie wielokąty dla kwadratów

Mistrzowskie kwadraty przez (8,8)
	0	1	2	3	4	5	6	7	8
1
2
3
4
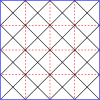
5
6
7
8

Złożenie operacji Goldberga-Coxetera odpowiada mnożeniu liczb zespolonych. sol do za $d} \ lewo ($ (tzn. seria operacji po lewej stronie daje wykres izomorficzny do wykresu po prawej), to dla graf 3-regularny ${\ Displaystyle (a + bu) (c + du)}$ jest w klasie równoważności ${\ Displaystyle (e + fu)}$ i dla a 4 -regularny wykres ${\ Displaystyle (a + bi) (c + di)}$ jest w klasie równoważności ${\ Displaystyle (e + fi)}$ . Ma to kilka użytecznych konsekwencji:

Zastosowanie powtarzanych operacji Goldberga-Coxetera jest przemienne i asocjacyjne .
Złożona koniugacja elementu $b$ za $bu}$ odpowiada odbiciu skonstruowanego
Ponieważ zarówno liczby całkowite Gaussa, jak i euklidesowe są domenami euklidesowymi , elementy tych domen można jednoznacznie rozłożyć na elementy pierwsze. Dlatego sensowne jest również rozłożenie operatora Goldberga-Coxetera na sekwencję „głównych” operatorów Goldberga-Coxetera, a ta sekwencja jest wyjątkowa (aż do przegrupowania).

Wykonanie konstrukcji GC

Etapy wykonywania konstrukcji GC $\ Displaystyle GC_ {k, \ ell} (G_ {0})}$ następujące: sol

$Określ$ główny wielokąt na podstawie $\ displaystyle$ i sol ${0}}$
Jeśli pracujesz na grafie 3- lub 4-regularnym (zamiast wykresu z trójkątnymi/kwadratowymi ścianami), weź jego graf podwójny . Ten podwójny wykres będzie miał trójkątne lub czworoboczne ściany.
Zastąp ściany triangulowanego/poczwórnego wykresu głównym wielokątem. Należy pamiętać, że grafy planarne mają „zewnętrzną” ścianę, którą również należy wymienić. W poniższym przykładzie odbywa się to poprzez dołączenie go do jednej strony wykresu i połączenie innych boków w razie potrzeby. To tymczasowo wprowadza do wykresu zachodzące na siebie krawędzie, ale wynikowy wykres jest płaski. Wierzchołki można przestawiać tak, aby nie zachodziły na siebie krawędzie.
Jeśli oryginalny graf był grafem 3- lub 4-regularnym, weź wynik z kroku 3 podwójnie. W przeciwnym razie wynikiem kroku 3 jest konstrukcja GC.

$_$ przykład , w którym sześcianu _ Na ostatnich dwóch wykresach niebieskie linie to krawędzie $Displaystyle$ podczas gdy czarne linie to krawędzie $GC_ {1,1} (G_ {0}) }$ . (Linie kropkowane to normalne krawędzie wykresu, po prostu $narysowane$ inaczej, aby zachodzące na siebie krawędzie wykresu były bardziej widoczne). Czerwone wierzchołki są w pozostają w ${\ displaystyle GC_ {1 , 1} (G_ {0})}$ , podczas gdy niebieskie wierzchołki są nowo tworzone przez konstrukcję i są tylko w ${\ Displaystyle GC_ {1,1} (G_ {0})}$ .

Główny kwadrat (1,1)
Początkowy wielościan (sześcian)
${\ Displaystyle G_ {0}}$ , szkielet sześcianu
Pośredni etap konstruowania ${\ Displaystyle GC_ {1,1} (G_ {0})}$ .
Wynik po przegrupowaniu ${\ Displaystyle GC_ {1,1} (G_ {0})}$
Osadzenie wyniku ( dwunastościan rombowy )

Rozszerzenia

Konstrukcję Goldberga-Coxetera można łatwo rozszerzyć na niektóre grafy niepłaskie, takie jak grafy toroidalne . Operatory klasy III, ze względu na ich chiralność, wymagają grafu, który można osadzić na orientowalnej powierzchni , ale operatory klasy I i II mogą być używane na grafach nieorientowalnych.

Zobacz też

przypisy